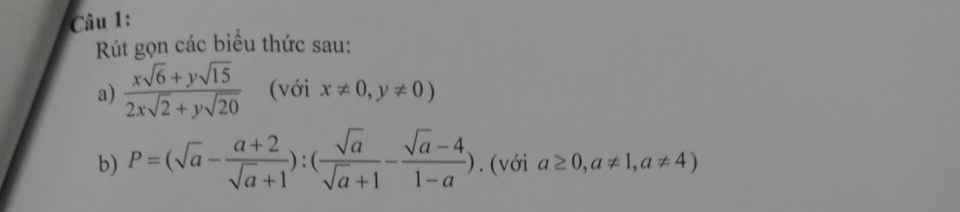Bạn làm thiếu rồi nhé. Đoạn này lúc đầu mình cũng phân vân nhưng vẫn tính được x và y
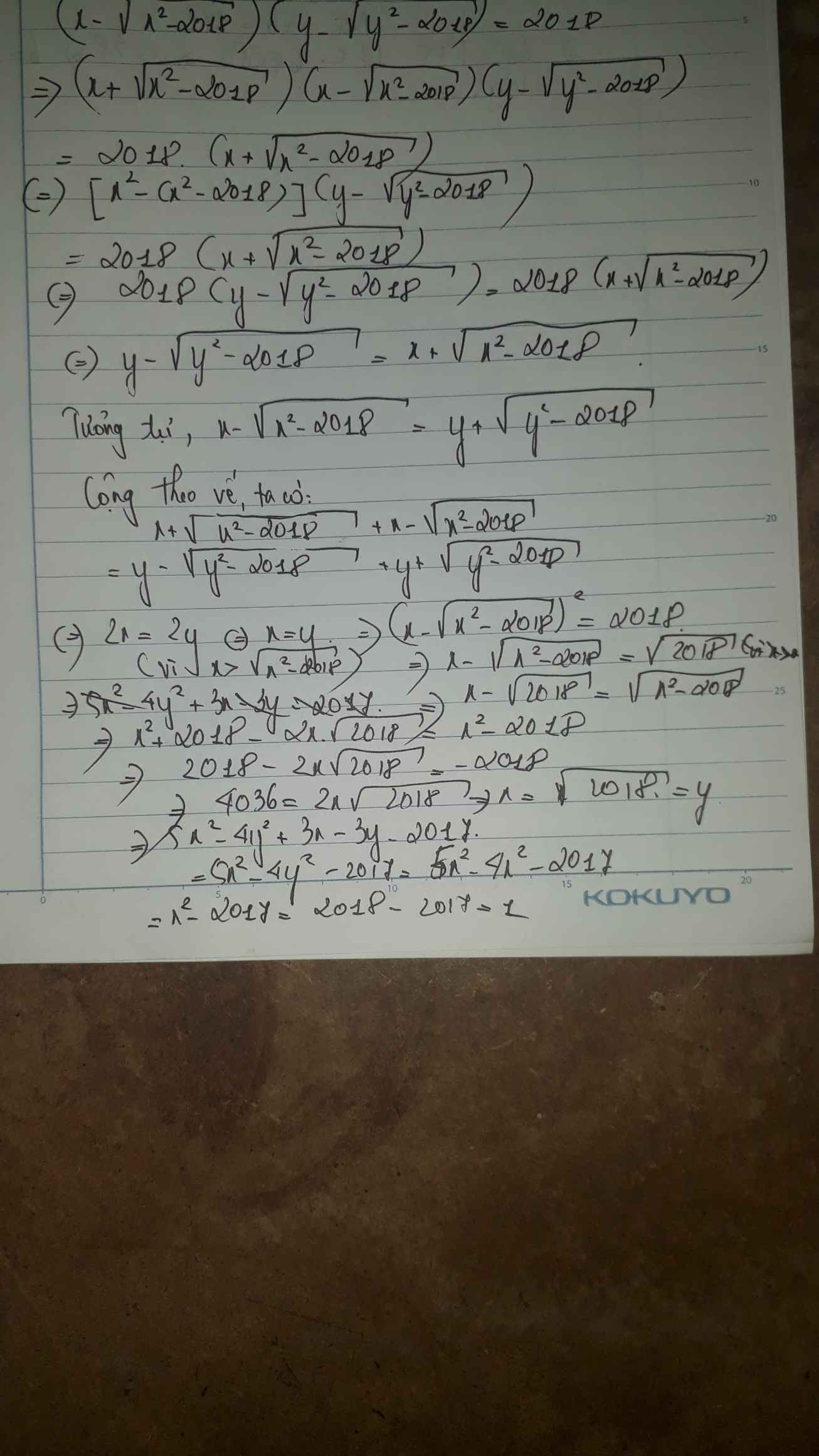
1.
ĐK: \(x,y\ge\sqrt{2018};x,y\le-\sqrt{2018}\)
\(\left(x-\sqrt{x^2-2018}\right)\left(y^2-2018\right)=2018\left(1\right)\)
\(\Leftrightarrow\left(x-\sqrt{x^2-2018}\right)\left(y-\sqrt{y^2-2018}\right)=2018\)
\(\Leftrightarrow2018\left(y-\sqrt{y^2-2018}\right)=2018\left(x+\sqrt{x^2-2018}\right)\)
\(\Leftrightarrow y-\sqrt{y^2-2018}=x+\sqrt{x^2-2018}\left(2\right)\)
Mặt khác:
\(\left(1\right)\Leftrightarrow2018\left(x-\sqrt{x^2-2018}\right)=2018\left(y+\sqrt{y^2-2018}\right)\)
\(\Leftrightarrow x-\sqrt{x^2-2018}=y+\sqrt{y^2-2018}\left(3\right)\)
Trừ vế theo vế (2) cho (3):
\(y-\sqrt{y^2-2018}-x+\sqrt{x^2-2018}=x+\sqrt{x^2-2018}-y-\sqrt{x^2-2018}\)
\(\Leftrightarrow x=y\)
Khi đó:
\(5x^2-4y^2+3x-3y-2017=x^2-2017\)
2.
Đặt \(AB=AC=BD=x\).
Dễ chứng minh được \(\Delta CAB\approx\Delta CDA\)
\(\Rightarrow\dfrac{CD}{AC}=\dfrac{AC}{BC}\)
\(\Leftrightarrow\dfrac{CD}{AC}=\dfrac{AC}{BD+CD}\)
\(\Leftrightarrow\dfrac{1}{x}=\dfrac{x}{x+1}\)
\(\Leftrightarrow x^2-x-1=0\)
\(\Leftrightarrow x=\dfrac{1+\sqrt{5}}{2}\left(\text{Vì }x>0\right)\)
\(\Rightarrow AB=\dfrac{1+\sqrt{5}}{2}\)


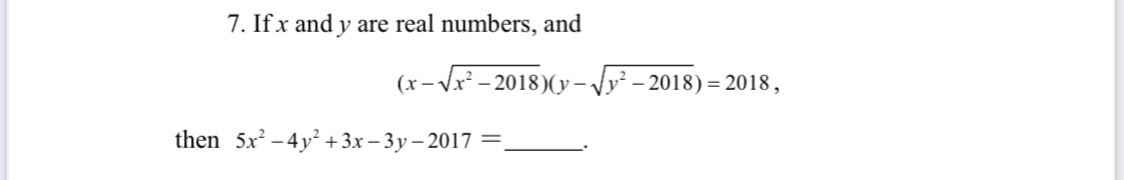












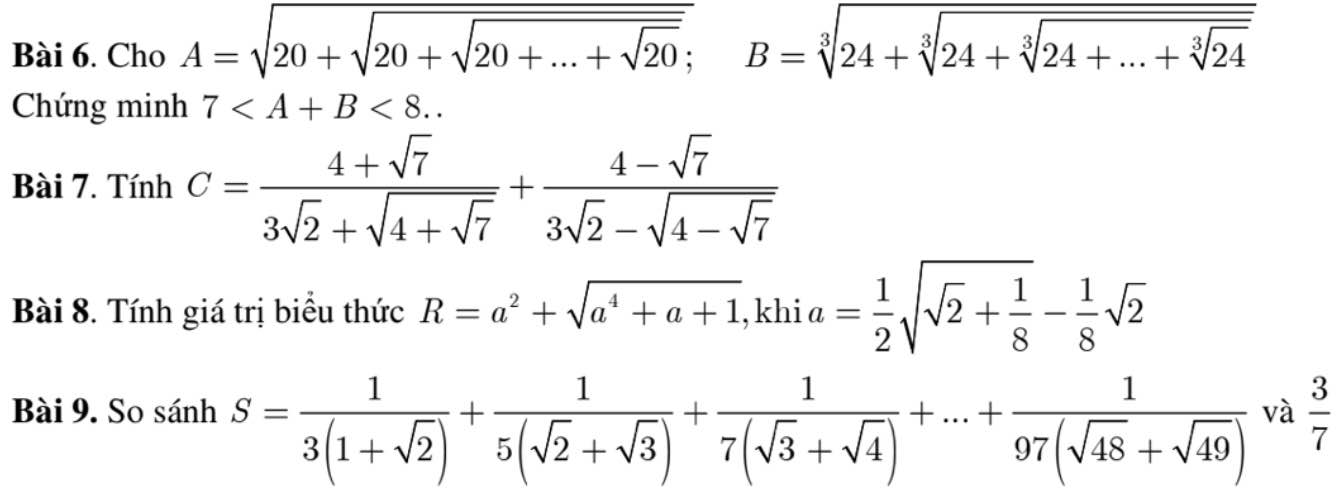
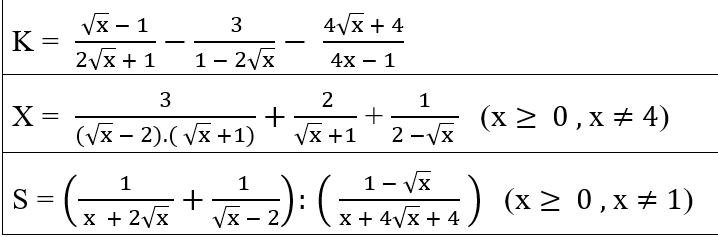

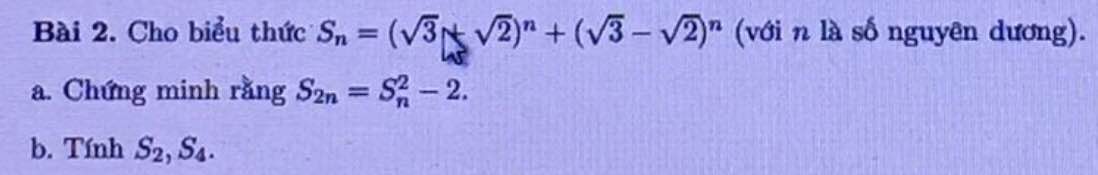 mọi người giải giúp em bài này với ạ 🥺
mọi người giải giúp em bài này với ạ 🥺