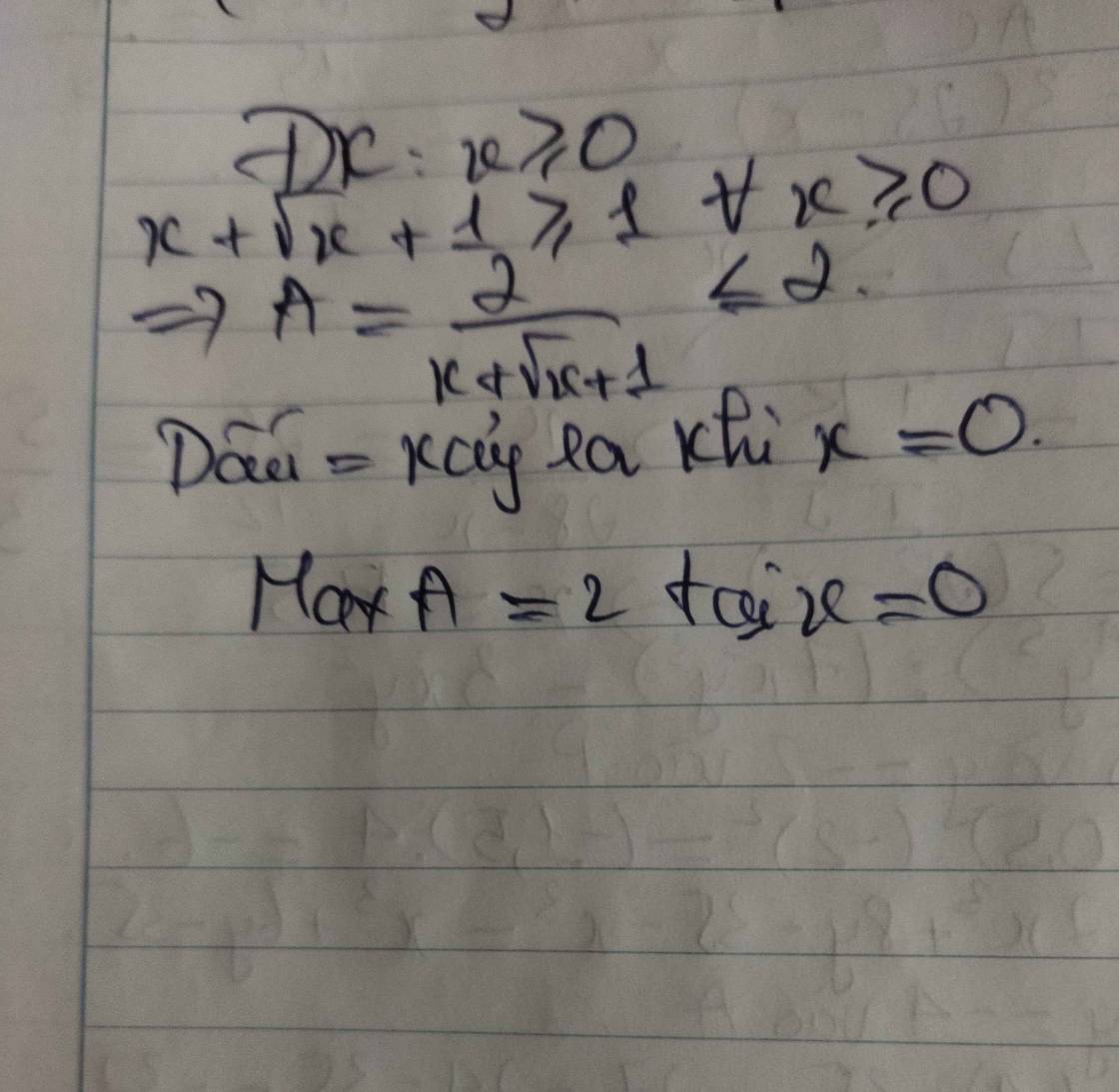tích mình với

ai tích mình

mình tích lại

thanks

Tích mình đi mình tích lại

câu 1 

ta có .....

lười viết Min - cốp xki nha

DKXD của A, ta có \(x^{2\le5\Rightarrow-\sqrt{5}\le x\le\sqrt{5}}\)

mà \(3x\ge-3\sqrt{5}\)

mặt kkhác \(\sqrt{5-x^2}\ge0\Rightarrow A=3x+x\sqrt{5-x^2}\ge-3\sqrt{5}\)

min A= \(-3\sqrt{5}\)\(\Leftrightarrow x=-\sqrt{5}\)

ta có \(A^2\le25\)và ta cx có \(-5\le A\le5\)

nhưng dễ thấy \(A=-5\)không xảy ra, vô lí nên ...........bạn xem đoạn sau nhé ( tiếp phần kia )

\(1,yz\sqrt{x-1}=yz\sqrt{\left(x-1\right)\cdot1}\le yz\cdot\dfrac{x-1+1}{2}=\dfrac{xyz}{2}\)

\(zx\sqrt{y-2}=\dfrac{zx\cdot2\sqrt{2\left(y-2\right)}}{2\sqrt{2}}\le\dfrac{xyz}{2\sqrt{2}}\\ xy\sqrt{z-3}=\dfrac{xy\cdot2\sqrt{3\left(z-3\right)}}{2\sqrt{3}}\le\dfrac{xyz}{2\sqrt{3}}\)

\(\Leftrightarrow M\le\dfrac{\dfrac{xyz}{2}+\dfrac{xyz}{2\sqrt{2}}+\dfrac{xyz}{2\sqrt{3}}}{xyz}=\dfrac{xyz\left(\dfrac{1}{2}+\dfrac{1}{2\sqrt{2}}+\dfrac{1}{2\sqrt{3}}\right)}{xyz}=\dfrac{1}{2}+\dfrac{1}{2\sqrt{2}}+\dfrac{1}{2\sqrt{3}}\)

Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x-1=1\\y-2=2\\z-3=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=4\\z=6\end{matrix}\right.\)

\(2,N^2=\left(\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}\right)^2\\ \Leftrightarrow N^2\le\left(a+b+b+c+c+a\right)\left(1^2+1^2+1^2\right)\\ \Leftrightarrow N^2\le6\left(a+b+c\right)=6\sqrt{2}\\ \Leftrightarrow N\le\sqrt{6\sqrt{2}}\)

Dấu \("="\Leftrightarrow a=b=c=\dfrac{\sqrt{2}}{3}\)

\(dkxđ\Leftrightarrow\left\{{}\begin{matrix}-x^2+5x\ge0\\-x^2+3x+18\ge0\end{matrix}\right.\)\(\Rightarrow0\le x\le5\Rightarrow\left\{{}\begin{matrix}x\ge0\\x\le5\end{matrix}\right.\)

\(\Rightarrow A=\sqrt{5x-x^2}+\sqrt{18+3x-x^2}\)

\(\sqrt{5x-x^2}=\sqrt{-\left(x^2-5x+\dfrac{25}{4}-\dfrac{25}{4}\right)}=\sqrt{-\left[\left(x-\dfrac{5}{2}\right)^2-\dfrac{25}{4}\right]}=\sqrt{-\left(x-\dfrac{5}{2}\right)^2+\dfrac{25}{4}}\ge0\left(1\right)\)

\(dấu\) \("="\) \(xảy\) \(ra\Leftrightarrow x=5\)

\(\sqrt{-x^2+3x+18}=\sqrt{-\left(x^2-3x-18\right)}=\sqrt{-\left[x^2-3x+\dfrac{9}{4}-\dfrac{81}{4}\right]}=\sqrt{-\left(x-\dfrac{3}{2}\right)^2+\dfrac{81}{4}}\ge\sqrt{-\left(5-\dfrac{3}{2}\right)^2+\dfrac{81}{4}}=\sqrt{8}\left(2\right)\)

dấu"=" xảy ra \(< =>x=5\)

\(\left(1\right)\left(2\right)\Rightarrow A\ge\sqrt{8}\) \(dấu\) \("="\) \(xảy\) \(ra\Leftrightarrow x=5\)\(\Rightarrow MinA=\sqrt{8}\)

\(\left(maxA=\sqrt{48}\right)dấu\) \("="\) \(xảy\) \(ra\Leftrightarrow x=\dfrac{15}{7}\)

\(\)

ĐKXĐ: \(x\ge0\)

Do \(\left\{{}\begin{matrix}2>0\\x+\sqrt{x}+1>0\end{matrix}\right.\) nên \(A_{max}\) khi \(x+\sqrt{x}+1\) đạt GTNN

Mà \(x\ge0\Rightarrow x+\sqrt{x}+1\ge1\)

\(\Rightarrow\dfrac{2}{x+\sqrt{x}+1}\le2\)

Hay \(A_{max}=2\) khi \(x=0\)

1, A= y^3(1-y)^2 = 4/9 . y^3 . 9/4 (1-y)^2

= 4/9 .y.y.y . (3/2-3/2.y)^2

=4/9 .y.y.y (3/2-3/2.y)(3/2-3/2.y)

<= 4/9 (y+y+y+3/2-3/2.y+3/2-3/2.y)^5

=4/9 . 243/3125

=108/3125

Đến đó tự giải

Thử sức với bài 1 xem thế nào :vv
x>0 => 0<x<=1 
f(x)=x^2(1-x)^3
Xét f'(x) = -(x-1)^2x(5x-2) 
Xét f'(x)=0 -> nhận x=2/5 và x=1thỏa mãn đk trên .
 Thử x=1 và x=2/5 nhận x=2/5 hàm số Max tại ddk 0<x<=1 (vậy x=1 loại)
P/s: HS cấp II hong nên làm cách này nhé em :vv 
 

Lời giải:
a.

Áp dụng BĐT Bunhiacopxky:

$A^2=(\sqrt{x-1}+\sqrt{9-x})^2\leq (x-1+9-x)(1+1)=16$

$\Rightarrow A\leq 4$

Vậy $A_{\max}=4$. Giá trị này đạt tại $x=5$

b.

$A=\frac{3(\sqrt{x}+2)+5}{\sqrt{x}+2}=3+\frac{5}{\sqrt{x}+2}$

Để $A$ nguyên thì $\frac{5}{\sqrt{x}+2}=m$ với $m$ nguyên dương

$\Leftrightarrow \sqrt{x}+2=\frac{5}{m}$

$\sqrt{x}=\frac{5-2m}{m}$

Vì $\sqrt{x}\geq 0$ nên $\frac{5-2m}{m}\geq 0$

Mà $m$ nguyên dương nên $5-2m\geq 0$

$\Leftrightarrow m\leq 2,5$. 

$\Rightarrow m=1; 2$

$\Rightarrow x=9; x=\frac{1}{4}$

a: ĐKXĐ: x>=0; x<>1

\(P=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right)\cdot\dfrac{\left(x-1\right)^2}{2}\)

\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(x-1\right)^2}{2}\)

\(=\dfrac{x-\sqrt{x}-2-x-\sqrt{x}+2}{2}\cdot\dfrac{x-1}{\sqrt{x}+1}\)

\(=-\sqrt{x}\left(\sqrt{x}-1\right)\)

b: 0<x<1

=>căn x<1

=>căn x-1<0

=>căn x*(căn x-1)<0

=>-căn x*(căn x-1)>0

=>P>0

c: \(P=-x+\sqrt{x}-\dfrac{1}{4}+\dfrac{1}{4}\)

\(=-\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{1}{4}< =\dfrac{1}{4}\)

Dấu = xảy ra khi x=1/4