cho tam giác ABC có AB =AC ,M là trung điểm của BC chứng minh rằng AM vuông góc với BC .các bạn giúp mình giải với

Những câu hỏi liên quan
Tam giác ABC có AB = AC, M là trung điểm của BC. Chứng minh rằng AM vuông góc với BC.
Các bạn giúp mình với, nhanh nhé ! Mình đang cần gấp !
Xét ΔABC có: AB=AC(gt)
=> ΔABC cân tại A
=>^B=^C
Xét ΔAMB và ΔAMC có:
AB=AC(gt)
^B=^C(cmt)
MB=MC(gt)
=> ΔAMB =ΔAMC( c.g.c)
=> ^AMB=^AMC
Mà ^AMB+^AMC=180( cặp góc kề bù)
=> ^AMB=^AMC=90
=>AM\(\perp\) BC
Đúng 0
Bình luận (0)
Ai giúp mình với !!!
a) Cho tam giác ABC, kẻ AH vuông góc với BC, nối A với trung điểm M của BC. Biết góc BAH = góc HAM = góc MAC và AB<AC. Tính số đo các góc của tam giác ABC.
b) Chứng minh rằng tam giác ABC vuông tại A. M là trung điểm của BC. Chứng minh AM = MB = MC.
Cho tam giác ABC có AB = AC, M là trung điểm của BC. Chứng minh rằng AM vuông góc với BC.
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
Đúng 0
Bình luận (1)
Lời giải:
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$BM=CM=\frac{BC}{2}$
$AM$ chung
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
$\Rightarrow \widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$
$\Rightarrow \widehat{AMB}=\widehat{AMC}=\frac{180^0}{2}=90^0$
$\Rightarrow AM\perp BC$.
Đúng 0
Bình luận (0)
cho tam giác ABC có góc A tù. trong góc A vẽ các đoạn ad, ae sao cho AD vuông góc với ab và ad=ab; ae vuông góc với ac và ae=ac. gọi m là trung điểm của DE, chứng minh rằng am vuông góc với bc.
các bạn làm giùm mình với. ko cần vẽ hình .
Cho Tam Giác ABC có AB=AC, M là trung điểm của BC. Chứng minh rằng AM vuông góc với BC
cho tam giác ABC có AB = AC. M là trung điểm của BC. Chứng minh rằng AM vuông góc với BC
cho tam giác abc có ac=ab gọi m ;à trung điểm bc trên tia đối tia ma lấy điểm d sao cho md=ma
a)chứng minh am vuông góc với bc và am là tia phân giác của góc bac
b)chứng minh md song song ac
các bạn giúp mình với mình đang rất cần vẽ luôn hình giúp mink nha
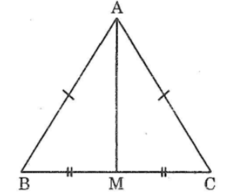
Tam giác ABC có AB = AC, M là trung điểm của BC. Chứng minh rằng AM vuông góc với BC.
Xét ΔAMB và ΔAMC, ta có:
AB = AC (gt)
BM = CM (vì M là trung điểm BC)
AM cạnh chung
Suy ra: ΔAMB= ΔAMC(c.c.c)
⇒ ∠(AMB) =∠(AMC) ̂(hai góc tương ứng)
Ta có: ∠(AMB) +∠(AMC) =180o (hai góc kề bù)
∠(AMB) =∠(AMC) =90o. Vậy AM ⏊ BC
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = AC , M là trung điểm của BC.
a ) Chứng minh : Tam giác ABM bằng tam giác ACM .
b) Chứng minh : AM là tia phân giác của góc BAC.
c ) Chứng minh : AM vuông góc với BC tại M. giúp mik vs
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
Đúng 0
Bình luận (0)
\(a,\) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
\(AB=AC\) (giả thiết)
\(AM\) là cạnh chung
\(BM=CM\) (giả thiết)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.c.c\right)\)
\(b,\) Vì \(\Delta ABM=\Delta ACM\) (chứng minh câu \(a\))
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\) (\(2\) góc tương ứng)
\(\Rightarrow AM\) là tia phân giác \(\widehat{BAC}\)
\(c,\) Vì \(\Delta ABC\) cân tại \(A\) (giả thiết)
Mà \(AM\) là tia phân giác \(\widehat{BAC}\) (chứng minh câu \(b\))
\(\Rightarrow AM\) là đường trung trực \(\Delta ABC\)
\(\Rightarrow AM\perp BC\) tại \(M\)
Đúng 2
Bình luận (0)
















