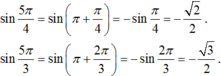giá trị 4 cung của hàm số lượng giác là gì ạ

Những câu hỏi liên quan
Bài 1: + Gía trị lượng giác là gì? Nó khác với tỉ số lượng giác như thế nào? Lấy ví dụ giúp mình để dễ hiểu ạ + Ví dụ sinB 0,2 thì con số 0,2 này được gọi là gì? + Với đề bảo tính sinB, cosB,... thì đây là tính ra số có phải không ạ? Hay: tính giá trị góc B, tính giá trị lượng giác góc B thì giá trị và giá trị lượng giác là như nào? + Khi nào thì tính ra góc, khi nào thì tính ra số? + Sau các tỉ số lượng giác là góc đúng không ạ? Còn có cái gì khác nữa không hay chỉ có mỗi góc thôi? ****** Các...
Đọc tiếp
Bài 1:
+ Gía trị lượng giác là gì? Nó khác với tỉ số lượng giác như thế nào? Lấy ví dụ giúp mình để dễ hiểu ạ
+ Ví dụ sinB = 0,2 thì con số 0,2 này được gọi là gì?
+ Với đề bảo tính sinB, cosB,... thì đây là tính ra số có phải không ạ? Hay: tính giá trị góc B", "tính giá trị lượng giác góc B thì giá trị và giá trị lượng giác là như nào?
+ Khi nào thì tính ra góc, khi nào thì tính ra số?
+ Sau các tỉ số lượng giác là góc đúng không ạ? Còn có cái gì khác nữa không hay chỉ có mỗi góc thôi?
****** Các bạn chỉ mình tất cả các dấu cộng mà mình liệt kê ra nhé! Còn những gì cần lưu ý các bạn chỉ mình ạ về phần này
Nêu định nghĩa các hàm số lượng giác. Chỉ rõ tập xác định và tập giá trị của từng hàm số đó.
a. Định nghĩa 1 : (Hàm số sin): Quy tắc tương ứng với mỗi số thực x với số thực sinx.
sin: R -> R
x -> y = sinx.
Hàm số y = sinx có tập xác định là R, tập giá trị là đoạn [-1;1].
b.Định nghĩa 2 : (Hàm số cosin): Quy tắc tương ứng với mỗi số thực x với số thực cosx.
cos : R -> R
x -> y = cosx.
Hàm số y = cosx có tập xác định là R, tập giá trị là đoạn [-1;1]
c. Định nghĩa 3: (Hàm số tang): Hàm số tang là hàm số được xác định bởi công thức
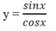
tan : D -> R
x -> y = tanx.
Hàm số y = tanx có tập xác định: 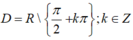
Tập giá trị của hàm số y = tanx là R.
d. Định nghĩa 4 : (Hàm số cotang): là hàm số được xác định bởi công thức
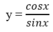
cot : D -> R
x -> y = cotx.
Hàm số y = cotx có tập xác định D = {x ∈ R \ x ≠ kπ, k ∈ Z}. Tập giá trị của hàm số y = cotx là tập R.
Đúng 0
Bình luận (0)
Tìm tập giá trị của hàm số lượng giác:\(y=5+2\sin x\)
\(Vì-1\le\sin x\le1\)
\(\Rightarrow-2\le2\sin x\le2\)
\(\Rightarrow3\le5+2\sin x\le7\)
\(\Rightarrow3\le y\le7\)
\(Vậy\) \(y_{max}=7\)
\(y_{min}=3\)
Đúng 2
Bình luận (0)
Giá trị của các hàm số lượng giác
sin
5
π
4
,
sin
5
π
3
lần lượt bằng
Đọc tiếp
Giá trị của các hàm số lượng giác sin 5 π 4 , sin 5 π 3 lần lượt bằng
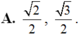
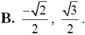
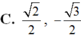
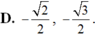
Nhắc lại khái niệm giá trị lượng giác của góc α, 0o ≤ α ≤ 180o.
Ta có thể mở rộng khái niệm giá trị lượng giác cho các cung và góc lượng giác.
Các số sinα; cosα; tanα; cotα được gọi là giá trị lượng giác của góc α, với 0o ≤ α ≤ 180o.
Đúng 0
Bình luận (0)
cho hàm số bậc nhất y=(m+3) x+7
a) Tìm giá trị của m để y là hàm số đồng biến
b) Tìm các giá trị của m để y là hàm số nghịch biến
giải chi tiết giúp mk vớiiiiii ạ
a. Hàm đồng biến khi:
\(m+3>0\Rightarrow m>-3\)
b. Hàm nghịch biến khi:
\(m+3< 0\Rightarrow m< -3\)
Đúng 1
Bình luận (0)
Đại lượng y có phải là hàm số của đại lượng x không, nếu bảng các giá trị tương ứng của chúng là:
x
4
4
9
16
y
-2
2
3
4
Đọc tiếp
Đại lượng y có phải là hàm số của đại lượng x không, nếu bảng các giá trị tương ứng của chúng là:
| x | 4 | 4 | 9 | 16 |
| y | -2 | 2 | 3 | 4 |
Trong bảng ta thấy ứng với giá trị x = 4 có hai giá trị khác nhau của y là 2 và -2. Theo định nghĩa thì y không phải là hàm số của đại lượng x.
Đúng 0
Bình luận (0)
Câu 1:Cho bảng giá trị sau. Chọn câu đúng
x -12 -3 10 12
y 4 4 4 4
A. Đại lượng y là không hàm số của đại lượng x
B. Đại lượng y là hàm số của đại lượng x
C. Đại lượng y tỉ lệ thuận với đại lượng x
D. Đại lượng y tỉ lệ nghịch với đại lượng x
Câu2:Cho bảng giá trị sau. Chọn câu đúng
x -12 -3 10 12
y 2 4 1 3
A. Đại lượng y là hàm số của đại lượng x
B. Đại lượng y là không hàm số của đại lượng x
C. Đại lượng y tỉ lệ thuận với đại lượng x
D. Đại lượng y tỉ lệ nghịch với đại lượng x
Câu3:Cho bảng giá...
Đọc tiếp
Câu 1:Cho bảng giá trị sau. Chọn câu đúng x -12 -3 10 12 y 4 4 4 4 A. Đại lượng y là không hàm số của đại lượng x B. Đại lượng y là hàm số của đại lượng x C. Đại lượng y tỉ lệ thuận với đại lượng x D. Đại lượng y tỉ lệ nghịch với đại lượng x Câu2:Cho bảng giá trị sau. Chọn câu đúng x -12 -3 10 12 y 2 4 1 3 A. Đại lượng y là hàm số của đại lượng x B. Đại lượng y là không hàm số của đại lượng x C. Đại lượng y tỉ lệ thuận với đại lượng x D. Đại lượng y tỉ lệ nghịch với đại lượng x Câu3:Cho bảng giá trị sau. Chọn câu đúng x -12 3 3 12 y 2 4 1 3 A. Đại lượng y tỉ lệ thuận với đại lượng x B. Đại lượng y tỉ lệ nghịch với đại lượng x C. Đại lượng y là không hàm số của đại lượng x D. Đại lượng y là hàm số của đại lượng x Câu4:Cho bảng giá trị sau. Chọn câu đúng x -12 -3 10 12 y 2 4 1 3 A. Đại lượng y là hàm số của đại lượng x B. Đại lượng y là không hàm số của đại lượng x C. Đại lượng y tỉ lệ thuận với đại lượng x D. Đại lượng y tỉ lệ nghịch với đại lượng x
Câu 1: A
Câu 2: C
Cau 3: B
Câu 4: C
Đúng 1
Bình luận (0)
Tính giá trị của hàm số lượng giác:
\(\tan\alpha+\cot\alpha=2\) ; \(0< \alpha< \dfrac{\pi}{2}\)
`0<α<π/2 => {(sinα>0),(cosα>0):}`
`tanα+cotα=2`
Mà `tanα.cotα=1`
`=>` \(\left\{{}\begin{matrix}tan\text{α}=1\\cot\text{α}=1\end{matrix}\right.\)
`=> α=π/4`
`=> sinα=cosα=\sqrt2/2`
Đúng 1
Bình luận (0)
Đại lượng x lấy các giá trị là các số tự nhiên. Đại lượng y lấy giá trị là ước của x. Đại lượng y có phải là hàm số của đại lượng x không?