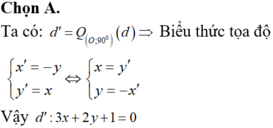Cho đường thẳng d có phương trình 2x - 3y +1 =0 và điểm O(0;0). Tìm phương trình đường thẳng d' đối xứng với d qua O

Những câu hỏi liên quan
Đường thẳng d đi qua điểm M(1, 2) và song song với đường thẳng delta: 2x+3y-12=0 có phương trình tổng quát là:
a. 4x+6y+1=0 b.2x+3y-8=0
c. 4x-3y-8=0 c. 2x+3y+8=0
Xem thêm câu trả lời
Trong mặt phẳng
v
→
(
−
2
;
1
)
cho, đường thẳng d có phương trình 2x − 3y + 3 0, đường thẳng
d
1
có phương trình
2
x
−
3
y
−
5
0...
Đọc tiếp
Trong mặt phẳng v → = ( − 2 ; 1 ) cho, đường thẳng d có phương trình 2x − 3y + 3 = 0, đường thẳng d 1 có phương trình 2 x − 3 y − 5 = 0 .
Viết phương trình của đường thẳng d’ là ảnh của d qua T v → .
Lấy một điểm thuộc d, chẳng hạn M = (0; 1).
Khi đó M′ = T v → ( M ) = (0 − 2; 1 + 1) = (−2; 2) thuộc d'.
Vì d' song song với d nên phương trình của nó có dạng 2x − 3y + C = 0.
Do M' ∈ d′ nên 2.(−2) − 3.2 + C = 0. Từ đó suy ra C = 10 .
Do đó d' có phương trình 2x − 3y + 10 = 0.
Đúng 0
Bình luận (0)
. Cho điểm A(1; 2) và đường thẳng d: 2x - 3y - 1 = 0 Viết phương trình đường thẳng delta đi qua A và vuông góc với d.
Lời giải:
VTPT của $(d)$: $(2,-3)$
Đường thẳng $\Delta$ vuông góc với $(d)$ nên VTCP của $(\Delta)$ chính là $(2,-3)$
$\Rightarrow$ VTPT $ của $(\Delta)$ là $(3,2)$
PTĐT $(\Delta)$: $3(x-1)+2(y-2)=0$
$\Leftrightarrow 3x+2y-7=0$
Đúng 1
Bình luận (0)
Câu 3. Cho điểm A(1; 2) và đường thẳng d: 2x - 3y - 1 = 0 Viết phương trình đường thẳng triangle delta*i qua A và song song với d.
Ta có: \(\Delta//d\Rightarrow\Delta:2x-3y+c=0\left(c\ne-1\right)\)
\(A\left(1;2\right)\in\Delta:2\cdot1-3\cdot2+c=0\)
\(\Leftrightarrow c=4\)
Vậy: \(\Delta:2x-3y+4=0\)
Đúng 2
Bình luận (0)
Vì (Δ)//d nên Δ: 2x-3y+c=0
Thay x=1 và y=2 vào Δ, ta được:
c+2-6=0
=>c=4
Đúng 1
Bình luận (0)
Bài 1: Lập phương trình đường thẳng d đối xứng với đường thẳng d qua đường thẳng Δ, với:a, d: 2x-y+10, Δ: 3x-4y+20b, d: x-2y+40, Δ: 2x+y-20c, d: x+y-10, Δ: x-3y+30 d, d: 2x-3y+10, Δ: 2x-3y-10 Bài 2: Lập phương trình đường thẳng d đối xứng với đường thẳng d qua điểm I với:a, d: 2x-y+10, I(2;1)b, d: x-2y+40, I(-3;0)c, d: x+y-10, I(0:3)d, d: 2x-3y+10, I trùng O(0;0)GIÚP EM VỚI Ạ!! EM ĐANG CẦN GẤP LẮM HUHUU T^T EM XIN CẢM ƠN!!!
Đọc tiếp
Bài 1: Lập phương trình đường thẳng d' đối xứng với đường thẳng d qua đường thẳng Δ, với:
a, d: 2x-y+1=0, Δ: 3x-4y+2=0
b, d: x-2y+4=0, Δ: 2x+y-2=0
c, d: x+y-1=0, Δ: x-3y+3=0
d, d: 2x-3y+1=0, Δ: 2x-3y-1=0
Bài 2: Lập phương trình đường thẳng d' đối xứng với đường thẳng d qua điểm I với:
a, d: 2x-y+1=0, I(2;1)
b, d: x-2y+4=0, I(-3;0)
c, d: x+y-1=0, I(0:3)
d, d: 2x-3y+1=0, I trùng O(0;0)
GIÚP EM VỚI Ạ!! EM ĐANG CẦN GẤP LẮM HUHUU T^T EM XIN CẢM ƠN!!!
mỗi bài, mk làm một phần ví dụ cho cậu nhé
nó đối xứng với nhau qua pt đường thẳng đenta,
trường hợp (d) ko cắt (đen ta) hay (d) cắt (đen ta) thì đều làm theo phương pháp sau
lấy 2 điểm bất kì thuộc (d) thì ta có như sau: A(0:1) là điểm thuộc đường thẳng (d)
lấy A' đối xứng với A qua (đen ta)
liên hệ tính chất đối xứng qua đường thẳng thì hiểu là AA' vuông góc (đen ta)
đồng thời giao điểm của AA' với (đen ta) là trung điểm của AA'
dễ dàng tìm đc giao điểm của (đen ta) với (d) là K(-2/5;1/5)
từ pt (đenta) thì dễ dàng =) vecto pháp tuyến của (đenta) =) (3;-4)
vì AA' vuông góc với (đenta) nên =) vectơ pháp tuyến của AA' là (4;-3)
áp véctơ pháp tuyến của AA' vào phương trình tổng quát đc: 4(x-0)-3(y-1)=0 (=) 4x-3y+3=0
gọi I là giao điểm của AA' và (đenta) =) I(-6/7;-1/7)
mà I là trung điểm của AA'
chắc chắn cậu sẽ dễ dàng suy ra điểm A'
mà K và A' thuộc (d') nên dễ dàng =) phương trình của (d')
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x + 3y - 3 = 0. Ảnh của đường thẳng d qua phép vị tự tâm O tỉ số k = 2 biến đường thẳng d thành đường thẳng có phương trình là:
A. 2x + 3y - 6 = 0
B. 4x + 6y - 5 = 0
C. -2x - 3y + 3 = 0
D. 4x + 6y - 3 = 0
Trong mặt phẳng
v
→
(
−
2
;
1
)
cho, đường thẳng d có phương trình 2x − 3y + 3 0, đường thẳng
d
1
có phương trình
2
x
−
3
y
−
5
0
.
Tìm t...
Đọc tiếp
Trong mặt phẳng v → = ( − 2 ; 1 ) cho, đường thẳng d có phương trình 2x − 3y + 3 = 0, đường thẳng d 1 có phương trình 2 x − 3 y − 5 = 0 .
Tìm tọa độ của w → có giá vuông góc với đường thẳng d để d 1 là ảnh của d qua T w →
Lấy một điểm thuộc d, chẳng hạn M = (0; 1).
Đường thẳng d 2 qua M vuông góc với có vectơ chỉ phương là v → = ( 2 ; − 3 ) .
Do đó phương trình của
d
2
là 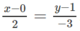 .
.
Gọi M' là giao của d 1 với d 2 thì tọa độ của nó phải thỏa mãn hệ phương trình:
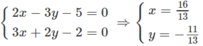
Từ đó suy ra
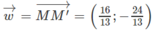
Đúng 0
Bình luận (0)
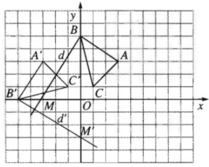
Trong mặt phẳng Oxy cho các điểm A(3; 3), B(0; 5), C(1; 1) và đường thẳng d có phương trình 5x − 3y + 15 = 0. Hãy xác định tọa độ các đỉnh của tam giác A’B’C’ và phương trình của đường thẳng d theo thứ tự là ảnh của tam giác ABC và đường thẳng d qua phép quay tâm O, góc quay 90 ο
Viết phương trình đường thẳng (d) đi qua điểm A\(\left(3;-1\right)\) và song song với đường thẳng (Δ): 2x + 3y - 1 = 0
\(\Delta:2x+3y-1=0.\)
\(\Rightarrow\) VTPT của \(\Delta\) là \(\overrightarrow{n_{\left(\Delta\right)}}=\left(2;3\right).\)
Phương trình đường thẳng \(\left(d\right)\) song song với đường thẳng \(\Delta:2x+3y-1=0.\)
\(\Rightarrow\) VTPT của đường thẳng \(\Delta\) cũng là VTPT của đường thẳng \(\left(d\right).\)
\(\Rightarrow\) VTPT của \(\left(d\right)\) là \(\overrightarrow{n_{\left(d\right)}}=\left(2;3\right).\)
Ta có đường thẳng \(\left(d\right)\) nhận \(\overrightarrow{n_{\left(d\right)}}=\left(2;3\right)\) làm VTPT; đi qua điểm \(A\left(3;-1\right).\)
\(\Rightarrow\) Phương trình đường thẳng \(\left(d\right)\) là:
\(2\left(x-3\right)+3\left(y+1\right)=0.\\ \Leftrightarrow2x-6+3y+3=0.\\ \Leftrightarrow2x+3y-3=0.\)
Đúng 1
Bình luận (0)
Trong mặt phẳng Oxy cho đường thẳng d:2x-3y+1=0 Viết phương trình đường thẳng d' là ảnh của d qua phép tâm O góc 900
A. d': 3x+2y+1=0
B. d': 3x-2y+1=0
C. d': 3x-2y-1=0
D. d': 3x+2y-1=0