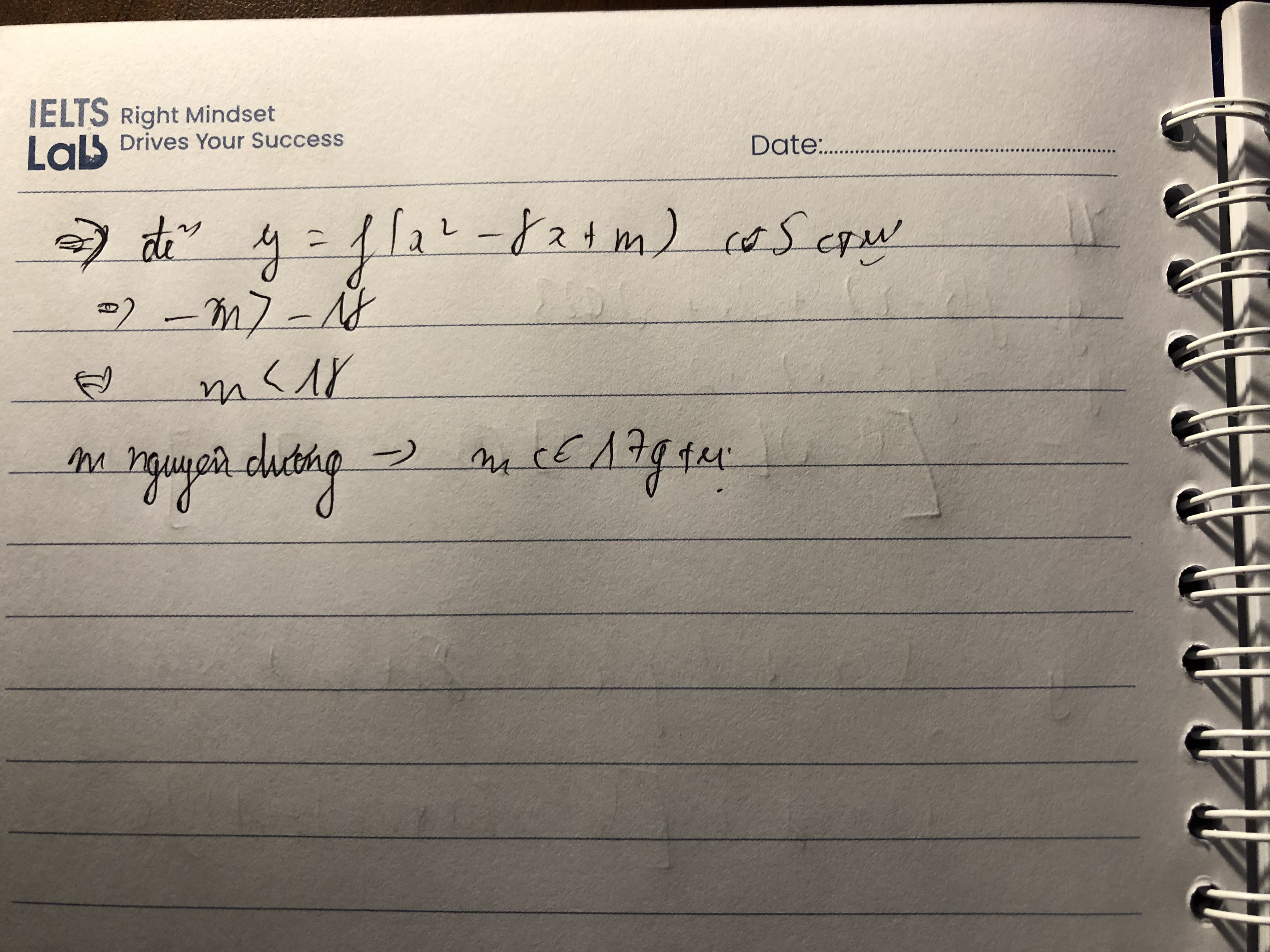giúp mình giải bài toán : chứng minh hàm số \(f\left(x\right)=cos2x-2x+3\) nghịch biến trên R

Những câu hỏi liên quan
Chứng minh hàm số : \(y=f\left(x\right)=3^x\left(x-\sqrt{x^2+1}\right)\) nghịch biến trên R
Ta có : \(f'\left(x\right)=\left(3^x\ln3\right)\left(x-\sqrt{x^2+1}\right)+3^x\left(1-\frac{x}{\sqrt{x^2+1}}\right)=3^x\left(x-\sqrt{x^2+1}\right)\left(\ln3-\frac{1}{\sqrt{x^2+1}}\right)\)
Mà : \(\begin{cases}\sqrt{x^2+1}>\sqrt{x^2}=\left|x\right|\ge x\Rightarrow x-\sqrt{x^2+1}< 0\\\ln3>1>\frac{1}{\sqrt{x^2+1}}\Rightarrow\ln3-\frac{1}{\sqrt{x^2+1}}>0\end{cases}\)
\(\Rightarrow f'\left(x\right)< 0\) với mọi x thuộc R
Vậy hàm số \(y=f\left(x\right)=3^x\left(x-\sqrt{x^2+1}\right)\) nghịch biến trên R
Đúng 0
Bình luận (0)
1
cho hàm số y=f (x)=-2x chứng minh hàm số nghịch biến trên tập số thực R
Gọi x1, x2 là hai giá trị của x (x1>x2)
Ta có: x1>x2\(\Leftrightarrow\)-2x1<-2x2 \(\Leftrightarrow\)f(x1) < f(x2)
Vì x1>x2 mà f(x1) < f(x2) suy ra hàm số nghịch biến trên tập hợp số thực R
Đúng 2
Bình luận (0)
Vì a=-2
nên hàm số y=-2x nghịch biến trên R
Đúng 0
Bình luận (0)
xét tính đồng biến nghịch biến của các hàm số trên
\(y=f\left(x\right)=x^2-2x+3\) trên khoảng \(_{\left(1;+\infty\right)}\)
y=f(x)=\(\sqrt{3-x}\) trên khoảng \(\left(-\infty;3\right)\)
Bài 10. Xét tính đồng biến và nghịch biến của các hàm số sau trên các khoảng đã chỉ raa: fleft(xright)2x^2-4x+3 trên các khoảng left(3;+inftyright) và (-10;1)b: fleft(xright)-3x^2+6x+1 trên các khoảng left(1;+inftyright) và (-10;-2)c: fleft(xright)dfrac{x}{x-2} trên khoảng left(-infty;2right)d: fleft(xright)-dfrac{1}{x+1} trên các khoảng (-3;-2) và left(-1;+inftyright)e: fleft(xright)x^{2020}+x^2-3 trên khoảng left(0;+inftyright)
Đọc tiếp
Bài 10. Xét tính đồng biến và nghịch biến của các hàm số sau trên các khoảng đã chỉ ra
a: \(f\left(x\right)=2x^2-4x+3\) trên các khoảng \(\left(3;+\infty\right)\) và (-10;1)
b: \(f\left(x\right)=-3x^2+6x+1\) trên các khoảng \(\left(1;+\infty\right)\) và (-10;-2)
c: \(f\left(x\right)=\dfrac{x}{x-2}\) trên khoảng \(\left(-\infty;2\right)\)
d: \(f\left(x\right)=-\dfrac{1}{x+1}\) trên các khoảng (-3;-2) và \(\left(-1;+\infty\right)\)
e: \(f\left(x\right)=x^{2020}+x^2-3\) trên khoảng \(\left(0;+\infty\right)\)
a) Đk:\(x\in R\)
TH1:Xét \(x\in\left(3;+\infty\right)\)
Lấy \(x_1;x_2\in\left(3;+\infty\right)\) thỏa mãn \(x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{2x_1^2-4x_1+3-\left(2x_2^2-4x_2+3\right)}{x_1-x_2}\)\(=2\left(x_1+x_2\right)-4\)
Do \(x_1;x_2\in\left(3;+\infty\right)\)\(\Rightarrow2\left(x_1+x_2\right)>12\Leftrightarrow2\left(x_1+x_2\right)-4>8>0\)
\(\Rightarrow I>0\)
Hàm đồng biến trên \(\left(3;+\infty\right)\)
TH2:Xét \(x\in\left(-10;1\right)\)
Lấy \(x_1;x_2\in\left(-10;1\right):x_1\ne x_2\)
Xét \(I=2\left(x_1+x_2\right)-4\)
Do \(x_1< 1;x_2< 1\Rightarrow2\left(x_1+x_2\right)< 4\Rightarrow I=2\left(x_1+x_2\right)-4< 0\)
Hàm nb trên khoảng \(\left(-10;1\right)\)
b)Làm tương tự,hàm nb trên \(\left(1;+\infty\right)\) và đb trên \(\left(-10;-2\right)\)
c)Đk: \(x\in R\backslash\left\{2\right\}\)
=>Hàm số xác định trên \(\left(-\infty;2\right)\)
Lấy \(x_1;x_2\in\left(-\infty;2\right):x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\dfrac{x_1}{x_1-2}-\dfrac{x_2}{x_2-2}}{x_1-x_2}=\dfrac{-2}{\left(x_1-2\right)\left(x_2-2\right)}\)
Do \(x_1;x_2< 2\Rightarrow\left(x_1-2\right)\left(x_2-2\right)>0\)
\(\Rightarrow I=-\dfrac{2}{\left(x_1-2\right)\left(x_2-2\right)}< 0\)
Hàm nb trên \(\left(-\infty;2\right)\)
d)\(I=\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}\)
Hàm đb trên \(\left(-1;+\infty\right)\) ; \(\left(-3;-2\right)\)
e)TXĐ:D=R
Lấy \(x_1;x_2\in\left(0;+\infty\right):x_1< x_2\)
\(T=f\left(x_1\right)-f\left(x_2\right)=x_1^{2020}+x_1^2-3-x_2^{2020}-x_2^2+3=x_1^{2020}-x_2^{2020}+x_1^2-x_2^2\)
Do \(x_1< x_2\Rightarrow x_1^{2020}< x_2^{2020};x_1^2< x_2^2\)
\(\Rightarrow T=x_1^{2020}-x_2^{2020}+x_1^2-x_2^2< 0\)
Hàm đb trên \(\left(0;+\infty\right)\)
Đúng 5
Bình luận (0)
Bài 7 (trang 46 SGK Toán 9 Tập 1)
Cho hàm số $y=f(x)=3 x$.
Cho $x$ hai giá trị bất kì $x_{1}, x_{2}$ sao cho $x_{1}<x_{2}$. Hãy chứng minh $f\left(x_{1}\right)<f\left(x_{2}\right)$ rồi rút ra kết luận hàm số đã cho đồng biến trên $\mathbb{R}$.
f(x1)=3x1f(x1)=3x1
f(x2)=3x2f(x2)=3x2
Theo giả thiết, ta có:
x1<x2⇔3.x1<3.x2x1<x2⇔3.x1<3.x2 ( vì 3>03>0 nên chiều bất đẳng thức không đổi)
⇔f(x1)<f(x2)⇔f(x1)<f(x2) (vì f(x1)=3x1;f(x1)=3x1;f(x2)=3x2)f(x2)=3x2)
Vậy với x1<x2x1<x2 ta được f(x1)<f(x2)f(x1)<f(x2) nên hàm số y=3xy=3x đồng biến trên RR.
Chú ý:
Ta cũng có thể làm như sau:
Vì x1<x2x1<x2 nên x1−x2<0x1−x2<0
Từ đó: f(x1)−f(x2)=3x1−3x2=3(x1−x2)<0f(x1)−f(x2)=3x1−3x2=3(x1−x2)<0
Hay f(x1)<f(x2)f(x1)<f(x2)
Vậy với x1<x2x1<x2 ta được f(x1)<f(x2)f(x1)<f(x2) nên hàm số y=3xy=3x đồng biến trên R
Do \(x_1< x_2\Rightarrow3x_1< 3x_2\)
\(\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)
Hàm số \(f\)đồng biến trên \(ℝ\)khi :
\(\forall x_1,x_2\inℝ\): \(x_1< x_2\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)
=> Hàm số đã cho đồng biến trên \(ℝ\)
Cho x các giá trị bất kì x1, x2 sao cho x1 < x2
=> x1 - x2 < 0
Ta có: f(x1) = 3x1 ; f( x2) = 3x2
=> f(x1) - f(x2) = 3x1 - 3x2 = 3(x1 - x2) < 0
=> f(x1) < f(x2)
Vậy với x1 < x2 ta được f(x1) < f(x2) nên hàm số y = 3x đồng biến trên tập hợp số thực R.
Xem thêm câu trả lời
Giúp em giải bài này với
Cho hàm số y = f (x) =2x-3
a) Hàm số trên đồng biến hay nghịch biến trên R? vì sao?
b) Tính f (l) : f(3 phần 2)
c) Vẽ đồ thị hàm số y = 2x-3
d) với giá trị nào của m thì đồ thị hàm số y = (3m-1)x+2 song song với đồ thị hàm số thị hàm số y = 2x-5
Cho hàm số y=f(x)= \(\left(3m^2-m+3\right)x-m\)với \(x\inℝ\). Hỏi hàm số đã cho đồng biến hay nghịch biến trên R? Giải thích?
LỚP 4 KO BIẾT
Đồng biến vì \(3m^2-m+3\)luôn dương
Lý do: \(3m^2-m+3\)có \(b^2-4ac=1-4.9=-35< 0\)
Cho hàm số \(y=f\left(x\right)=4-\dfrac{2}{5}x\) với \(x\in\mathbb{R}\)
Chứng minh rằng hàm số đã cho nghịch biến trên \(\mathbb{R}\)
Câu 48: Cho hàm số yf(x) có đạo hàm liên tục trên R và fleft(xright)xleft(2x-1right)left(x^2+3right)+2. Hàm số yfleft(3-xright)+2x+2023 đồng biến trên khoảng nào trong các khoảng sau?A: left(-infty;3right)B: (3;5)C: (2;5/2)D: (5/2;3)Câu 50: Cho hàm số yf(x) có đạo hàm fleft(xright)left(x-1right)^2cdotleft(x^2-2xright) với forall xin R. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số fleft(x^2-8x+mright) có 5 điểm cực trị?
Đọc tiếp
Câu 48: Cho hàm số y=f(x) có đạo hàm liên tục trên R và \(f'\left(x\right)=x\left(2x-1\right)\left(x^2+3\right)+2\). Hàm số \(y=f\left(3-x\right)+2x+2023\) đồng biến trên khoảng nào trong các khoảng sau?
A: \(\left(-\infty;3\right)\)
B: (3;5)
C: (2;5/2)
D: (5/2;3)
Câu 50: Cho hàm số y=f(x) có đạo hàm \(f'\left(x\right)=\left(x-1\right)^2\cdot\left(x^2-2x\right)\) với \(\forall x\in R\). Có bao nhiêu giá trị nguyên dương của tham số m để hàm số \(f\left(x^2-8x+m\right)\) có 5 điểm cực trị?