Hãy cho biết số nào trong các số \(\dfrac{2}{3};\dfrac{2}{7};-\dfrac{4}{5}\) là nghiệm của bất phương trình :
\(5-3x< \left(4+2x\right)-1\)
Những câu hỏi liên quan
21 tháng 3 2022 lúc 9:22
Cho các phân số: \(\dfrac{3}{5};\dfrac{5}{6};\dfrac{25}{30};\dfrac{9}{15};\dfrac{10}{12};\dfrac{6}{10}.\)
a) Rút gọn các phân số trên ;
b) Cho biết trong trong các phân số trên có những phân số nào bằng nhau.
Giúp mình với, cần gấp
\(\dfrac{25}{30}=\dfrac{5}{6}\)
\(\dfrac{9}{15}=\dfrac{3}{5}\)
\(\dfrac{10}{12}=\dfrac{5}{6}\)
\(\dfrac{6}{10}=\dfrac{3}{5}\)
Đúng 1
Bình luận (0)
Bạn nhìn theo phần rút gọn tui gửi mà so sánh các phân số khác nhek
Đúng 0
Bình luận (0)
\(\dfrac{25}{30}=\dfrac{5}{6}\)
\(\dfrac{10}{12}=\dfrac{5}{6}\)
\(\dfrac{6}{10}=\dfrac{3}{5}\)
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Cho các phân số \(\dfrac{3}{4}\);\(\dfrac{7}{7}\);\(\dfrac{3}{2}\);\(\dfrac{4}{3}\)phân số nào lớn nhất trong các phân số đó
\(\dfrac{3}{2}\) lớn nhất vì các phân số còn lại < 1
Đúng 1
Bình luận (0)
Cho bốn phân số: \(\dfrac{17}{80}; \dfrac{611}{125}; \dfrac{133}{91}; \dfrac{9}{8}\)
a) Phân số nào trong những phân số trên không viết được dưới dạng số thập phân hữu hạn?
b) Cho biết \(\sqrt{2}=1,414213563...\), hãy so sánh phân số tìm được trong câu a) với \(\sqrt{2}\)
a)
Cách 1:
\(\dfrac{17}{80}=0,2125; \dfrac{611}{125}=4,888; \dfrac{133}{91}=1,(461538); \dfrac{9}{8}=1,125\)
Như vậy, trong những phân số trên, phân số không viết được dưới dạng số thập phân hữu hạn là: \(\dfrac{133}{91}\)
Cách 2: Vì các phân số trên đều tối giản và có mẫu dương
Ta có: \(80=2^4.5; 125=5^3; 91=7.13; 8=2^3\) nên chỉ có 91 có ước nguyên tố khác 2,5 nên \(\dfrac{133}{91}\) không viết được dưới dạng số thập phân hữu hạn
b) Ta có: \(\dfrac{133}{91} = 1,(461538) = 1,461538461538…..\)
Quan sát các chữ số ở các hàng tương ứng từ trái sang phải, vì 1= 1; 4 = 4; 1 < 6 nên 1,414213562...< 1,461538461538…..
Vậy \(\dfrac{133}{91}>\sqrt{2}\)
Đúng 0
Bình luận (0)
17 tháng 1 lúc 20:37
trong các phân số sau: \(\dfrac{1}{3}\), \(\dfrac{4}{7}\), \(\dfrac{8}{12}\), \(\dfrac{30}{36}\), \(\dfrac{72}{73}\)
a. Phân số nào là tối giản? vì sao?
b. Phân số nào rút gọn được. Hãy rút gọn phân số đó
a: Các phân số tối giản là \(\dfrac{1}{3};\dfrac{4}{7};\dfrac{72}{73}\) vì ƯCLN(1;3)=1; ƯCLN(4;7)=1; ƯCLN(72;73)=1
b:
Các phân số rút gọn được là
\(\dfrac{8}{12}=\dfrac{8:4}{12:4}=\dfrac{2}{3}\)
\(\dfrac{30}{36}=\dfrac{30:6}{36:6}=\dfrac{5}{6}\)
Đúng 1
Bình luận (0)
Em hãy tìm các cặp phân số bằng nhau trong các phân số sau:
\(\dfrac{2}{5};\dfrac{1}{3};\dfrac{3}{9};\dfrac{4}{{10}}\)
Tham khảo:
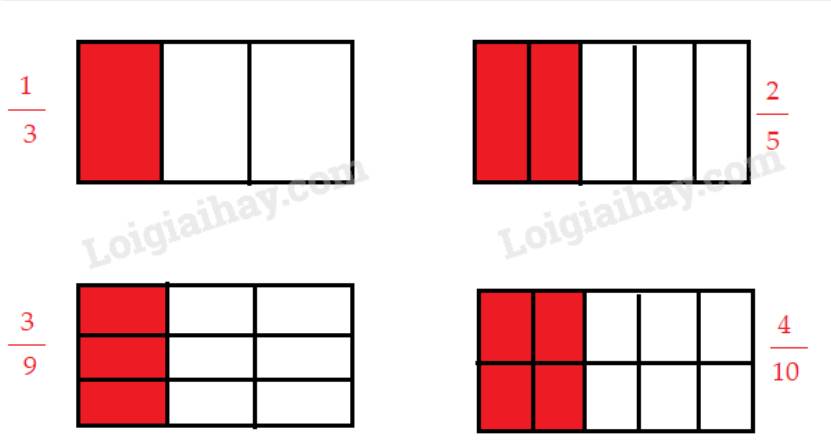
Như vậy,\(\dfrac{2}{5} = \dfrac{4}{{10}}\)
\(\dfrac{1}{3} = \dfrac{3}{9}\)
Đúng 0
Bình luận (0)
Hãy cho biết số nào trong các số 2/3 ; 2/7 ; -4/5 là nghiệm của bất phương trình 5 – 3x < (4 + 2x) – 1
Ta có: 5 – 3x < (4 + 2x) – 1 ⇔ 5 – 3x < 4 + 2x – 1
⇔ -3x – 2x < 4 – 1 – 5 ⇔ -5x < -2 ⇔ x > 2/5
Vậy chỉ có giá trị 2/3 > 2/5 nên trong các số đã cho thì số 2/3 là nghiệm của bất phương trình.
Đúng 0
Bình luận (0)
I. Trắc nghiệm:Câu 1: Trong các cách viết sau đây, cách viết nào không cho ta phân số?A. dfrac{0,5}{-4} B. dfrac{3}{13} C. dfrac{0}{8} D. dfrac{1}{-9}Câu 2: Các số sau, cách viết nào cho ta phân số.A. dfrac{2,3}{4} B. dfrac{-3}{5} C. dfrac{-2,3}{4,5} D. dfrac{9}{0}Câu 3: Số nghịch đảo của dfrac{-4}{7} là:A. -dfrac{4}{7} B. dfrac{4}{7} C. dfrac{7}{4} D. dfrac{-7}{4}Câu 4: Khi rút gọn phân số dfrac{-27}{63}ta được p/ số tối giản là:A. dfrac{-3}{7} B. dfrac{9}{21} C. dfrac{3}{...
Đọc tiếp
I. Trắc nghiệm:
Câu 1: Trong các cách viết sau đây, cách viết nào không cho ta phân số?
A. \(\dfrac{0,5}{-4}\) B. \(\dfrac{3}{13}\) C. \(\dfrac{0}{8}\) D. \(\dfrac{1}{-9}\)
Câu 2: Các số sau, cách viết nào cho ta phân số.
A. \(\dfrac{2,3}{4}\) B. \(\dfrac{-3}{5}\) C. \(\dfrac{-2,3}{4,5}\) D. \(\dfrac{9}{0}\)
Câu 3: Số nghịch đảo của \(\dfrac{-4}{7}\) là:
A. \(-\dfrac{4}{7}\) B. \(\dfrac{4}{7}\) C. \(\dfrac{7}{4}\) D. \(\dfrac{-7}{4}\)
Câu 4: Khi rút gọn phân số \(\dfrac{-27}{63}\)ta được p/ số tối giản là:
A. \(\dfrac{-3}{7}\) B. \(\dfrac{9}{21}\) C. \(\dfrac{3}{7}\) D. \(\dfrac{-9}{21}\)
Câu 5: Tổng của hai p/ số \(\dfrac{-7}{6}+\dfrac{15}{6}\)bằng:
A. \(\dfrac{-4}{3}\) B. \(\dfrac{4}{3}\) C. \(\dfrac{11}{3}\) D. \(\dfrac{-11}{3}\)
Câu 6: Kết quả của phép tính \(2,15+3,85\)
A. 7 B. 6 C. 5 D. 1,7
Câu 7: So sánh hai phân số \(\dfrac{1}{5}\) và \(\dfrac{-3}{5}\), kết quả là:
A. \(\dfrac{1}{5}< \dfrac{-3}{5}\) B. \(\dfrac{1}{5}>\dfrac{-3}{5}\) C. \(\dfrac{-1}{5}< \dfrac{-3}{5}\) D. \(\dfrac{-1}{5}< \dfrac{-3}{5}\)
Câu 8: Trong các p/ số \(\dfrac{-1}{7};\dfrac{3}{7}và\dfrac{2}{7}\), p/ số lớn nhất là:
A. \(\dfrac{-1}{7}\) B. \(\dfrac{1}{7}\) C. \(\dfrac{2}{7}\) D. \(-\dfrac{3}{7}\)
Câu 9: P/ số \(\dfrac{3}{100}\) được viết dưới dạng số thập phân là:
A. 0,3 B. 0,003 C. 0,03 D. 0,0003
Câu 10: Số 0,17 được viết dưới dạng phân số là:
A. \(\dfrac{17}{10}\) B. \(\dfrac{1,7}{10}\) C. \(\dfrac{1,7}{100}\) D. \(\dfrac{17}{100}\)
Câu 11: Kết quả của phép tính \(\dfrac{2}{5}+\dfrac{3}{7}\) là:
A. \(\dfrac{5}{12}\) B. \(\dfrac{5}{7}\) C. \(\dfrac{22}{35}\) D. \(\dfrac{22}{12}\)
Câu 12: Kết quả của phép tính:\(\dfrac{2}{5}.\dfrac{10}{3}\)là:
A. \(\dfrac{4}{3}\) B.\(\dfrac{4}{5}\) C. \(\dfrac{5}{2}\) D. \(\dfrac{3}{25}\)
Câu 13: Kết quả của phép tính 0,25.40 là:
A. 10 B. 1 C. 100 D. 1000
Câu 14: Làm tròn số 73465 đến hàng chục là:
A. 73465 B. 73500 C. 73460 D. 73470
Câu 15: Làm tròn số 312, 163 đến hàng trăm là:
A. 73465 B. 73500 C. 73460 D. 73470
Câu 16: Làm tròn số 312,163 đến hàng phần mười là:
A. 312,1 B. 312,2 C. 312,16 D, 312,17
Câu 17: Làm tròn số 29,153 đến hàng phần trăm là:
A. 29,1 B. 29,2 C. 29, 15 D. 29,16
Câu 18: Tỉ số của 3 và 7 là:
A. \(\dfrac{7}{3}\) B. \(\dfrac{3}{7}\) C. \(\dfrac{-3}{7}\) D. \(\dfrac{-7}{3}\)
Câu 19: Tỉ số phần trăm của 3 và 5 là:
A. \(\dfrac{3}{5}\) B. \(\dfrac{5}{3}\) C. \(60\%\) D. \(6\%\)
Câu 20: Đoạn thẳng AB có độ dài 5cm, đoạn thẳng CD có độ dài bằng 10cm. Tỉ số độ dài của đoạn thẳng AB và đoạn thẳng CD là:
A. \(\dfrac{5}{10}\) B. \(\dfrac{1}{2}\) C. 2 D. \(\dfrac{10}{5}\)
1. B và C
2. B
3. D
4.A
5.B
6.B
7.B
8.C
9.C
10.D
11.không có đáp án
12.A
13.A
14.D
Đúng 0
Bình luận (0)
1. B và C
2. B
3. D
4.A
5.B
6.B
7.B
8.C
9.C
10.D
11.không có đáp án
12.A
13.A
14.D
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Cho các số Q x,y,z :
x = \(\dfrac{a}{b};y=\dfrac{c}{d};z=\dfrac{m}{n}trong\) đó m= \(\dfrac{a+c}{2}\)
n = \(\dfrac{b+d}{2}\). Cho biết x\(\ne\)y, hãy so sánh y với z , z với x
Cho tỉ lệ thức \(\dfrac{3}{7} = \dfrac{9}{{21}}\). Hãy tính các tỉ số \(\dfrac{{3 + 9}}{{7 + 21}}\) và \(\dfrac{{3 - 9}}{{7 - 21}}\) rồi so sánh chúng với các tỉ số trong tỉ lệ thức đã cho.
Ta có tỉ thức : \(\dfrac{3}{7} = \dfrac{9}{{21}}\)
Xét \(\dfrac{{3 + 9}}{{7 + 21}}\) = \(\dfrac{{12}}{{28}}\) = \( = \dfrac{3}{7}\)( chia cả tử và mẫu cho 4 )
Xét \(\dfrac{{3 - 9}}{{7 - 21}}\) = \(\dfrac{{ - 6}}{{ - 14}}\)\( = \dfrac{3}{7}\)( chia cả tử và mẫu cho 2 )
Sau khi thực hiện tính các tỉ số ta thấy các kết quả sau khi tối giản của tỉ số bằng với các tỉ só trong tỉ lệ thức đã cho.
Đúng 0
Bình luận (0)