Đặt biểu thức trên là A.

Ta có : A = \(x^3+9x^2+27x+27\)

=> A = \(\left(x+3\right)^3\) ( hàng đẳng thức)

thay x = 97 \(\Leftrightarrow A=\left(97+3\right)^3=100^3=1000000\)

b/ Ta có \(G\left(x\right)=3x\left(x-1\right)-x+1\)

=> \(G\left(x\right)=3x\left(x-1\right)-\left(x-1\right)\)

=> \(G\left(x\right)=\left(x-1\right)\left(3x-1\right)\)

Khi G (x) = 0

=> \(\left(x-1\right)\left(3x-1\right)=0\)

=> \(\orbr{\begin{cases}x-1=0\\3x-1=0\end{cases}}\)=> \(\orbr{\begin{cases}x=1\\3x=1\end{cases}}\)=> \(\orbr{\begin{cases}x=1\\x=\frac{1}{3}\end{cases}}\)

Vậy G (x) có 2 nghiệm là \(\hept{\begin{cases}x=1\\x=\frac{1}{3}\end{cases}}\).

c/ Ta có \(H\left(x\right)=x^2-4x+3\)

=> \(H\left(x\right)=x^2-x-3x+3\)

=> \(H\left(x\right)=\left(x^2-x\right)-\left(3x-3\right)\)

=> \(H\left(x\right)=x\left(x-1\right)-3\left(x-1\right)\)

=> \(H\left(x\right)=\left(x-1\right)\left(x-3\right)\)

Khi H (x) = 0

=> \(\left(x-1\right)\left(x-3\right)=0\)

=> \(\orbr{\begin{cases}x-1=0\\x-3=0\end{cases}}\)=> \(\orbr{\begin{cases}x=1\\x=3\end{cases}}\)

Vậy H (x) có 2 nghiệm: \(\hept{\begin{cases}x=1\\x=3\end{cases}}\)

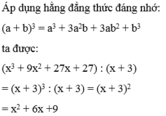
Vậy phép chia đã cho là phép chia hết có thương là:  x + 3 2 = x 2 + 6 x + 9

Chọn đáp án D

`#3107.101107`

`A(x) = 3x - 9x^2 + 4x + 5x^3 + 7x^2 + 1`

`= (3x + 4x) - (9x^2 - 7x^2) + 5x^3 + 1`

`= 7x - 2x^2 + 5x^3 + 1`

`B(x) = 5x^3 - 3x^2 + 7x + 10`

`A(x) - B(x) = 7x - 2x^2 + 5x^3 + 1 - (5x^3 - 3x^2 + 7x + 10)`

`= 7x - 2x^2 + 5x^3 + 1 - 5x^3 + 3x^2 - 7x - 10`

`= (7x - 7x) + (3x^2 - 2x^2) + (5x^3 - 5x^3) - (10 - 1)`

`= x^2 - 9`

`=> C(x) = x^2 - 9`

`C(x) = 0`

`=> x^2 - 9 = 0`

`=> x^2 = 9 => x^2 = (+-3)^2 => x = +-3`

Vậy, nghiệm của đa thức `C(x)` là `x \in {3; -3}.`

a)\(f\left(x\right)=5x^3-9x^2+2x+m=5x^2\left(x+2\right)-19x\left(x+2\right)+40\left(x+2\right)-80+m=\left(x+2\right)\left(5x^2-19x+40\right)+m-80\)

Để \(f\left(x\right)⋮g\left(x\right)\) thì \(m-80=0\Leftrightarrow m=80\)

b) \(f\left(x\right)=\left(x+2\right)\left(5x^2-19x+40\right)+m-80\)

Để f(x) chia g(x) có số dư bằng 3 thì \(m-80=3\Leftrightarrow m=83\)

9x^2 - 32 + k^2 - 2k.x = 0

Thay x = 2 vào, ta có: 

<=> 9.2^2 - 32 + k^2 - 2k.2 = 0

<=> 36 - 32 + k^2 - 4k = 0

<=> 4 + k^2 - 4k = 0

<=> (2 - k)^2 = 0

<=> 2 - k = 0

<=> k = 2

Tìm gì hả bạn ?

ta có:

\(9x^2-4=0\\ 9x^2=4\\ x^2=\dfrac{9}{4}\\ x=\sqrt{\dfrac{9}{4}}=\dfrac{3}{2}\)

\(\Rightarrow\)vậy...

\(\text{Đặt h(x)=0}\)

\(\Rightarrow9x^2-4=0\)

\(\Rightarrow9x^2=0+4=4\)

\(\Rightarrow x^2=4:9=\dfrac{4}{9}\)

\(\Rightarrow x=\sqrt{\dfrac{4}{9}}=\dfrac{2}{3}\)

\(\text{Vậy đa thức h(x) có 1 nghiệm là x=}\dfrac{2}{3}\)

a: \(\Leftrightarrow\left(x-5\right)\left(x+1\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\\x=1\end{matrix}\right.\)

d: \(\Leftrightarrow\left(x+3\right)\left(x^2-4x+5\right)=0\)

\(\Leftrightarrow x+3=0\)

hay x=-3