cách cộng hai đa thức khác số mũ

Những câu hỏi liên quan
1, viết đơn thức sau dưới dạng tổng của hai đơn thức trong đó có một đơn thức bằng 2x mũ 2 y mũ 3
A)5x mũ 2 y mũ 3
B)-6 x mũ 2 y mũ 3
C) m x mũ 2 y mũ 3 ( m là hằng số)
2) cho đa thức A(x)3 x mũ 2 + 5 x mũ 3 cộng x trừ 2 x mũ 2 trừ x mũ 3 cộng 1 trừ 4 x mũ 3 trừ 2X - 3
a) thu gọn đa thức
b) tìm x để giá trị của đa thức A(x) bằng giá trị của đa thức B(x) 2 x- 2
Đọc tiếp
1, viết đơn thức sau dưới dạng tổng của hai đơn thức trong đó có một đơn thức bằng 2x mũ 2 y mũ 3
A)5x mũ 2 y mũ 3
B)-6 x mũ 2 y mũ 3
C) m x mũ 2 y mũ 3 ( m là hằng số)
2) cho đa thức A(x)3 x mũ 2 + 5 x mũ 3 cộng x trừ 2 x mũ 2 trừ x mũ 3 cộng 1 trừ 4 x mũ 3 trừ 2X - 3
a) thu gọn đa thức
b) tìm x để giá trị của đa thức A(x) bằng giá trị của đa thức B(x) =2 x- 2
viết bằng công thức ở chỗ \(\sum\) đi bạn
Cho hai đa thức P( x ) = x mũ 2 cộng 5 x mũ 4 trừ 3 x mũ 3 cộng x mũ 2 cộng 4 x mũ 4 + 3 x mũ 3 - x + 5
Q(x) = x - 5 x mũ 3 trừ x mũ 2 trừ x mũ 4 + 4 x mũ 3 trừ x mũ 2 + 3 x - 1
Nêu cách cộng 2 lũy thừa khác cơ số và số mũ.
Anh tách mỗi lũy thừa ra và nhân lai rồi kết quả cộng với nhau anh ạ. Kết quả duy nhất ah
Đúng 1
Bình luận (0)
Cho hai đa thứcP(x) 5{x^2} + 4 + 2x và Q(x) 8x + {x^2} + 1.a) Sắp xếp các đa thức P(x), Q(x) theo số mũ giảm dần của biến.b) Tìm đơn thức thích hợp trong dạng thu gọn của P(x) và Q(x) cho ? ở bảng sau rồi cộng hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột:c) Dựa vào kết quả cộng hai đơn thức theo từng cột, xác định đơn thức R(x).
Đọc tiếp
Cho hai đa thức
\(P(x) = 5{x^2} + 4 + 2x\) và \(Q(x) = 8x + {x^2} + 1\).
a) Sắp xếp các đa thức P(x), Q(x) theo số mũ giảm dần của biến.
b) Tìm đơn thức thích hợp trong dạng thu gọn của P(x) và Q(x) cho ? ở bảng sau rồi cộng hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột:
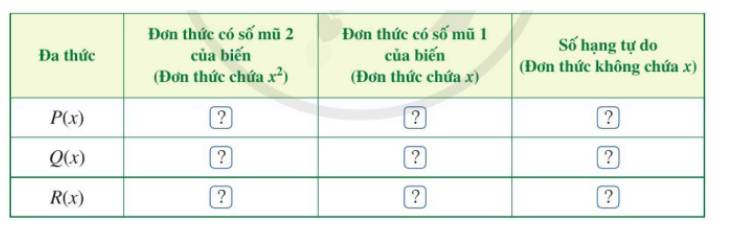
c) Dựa vào kết quả cộng hai đơn thức theo từng cột, xác định đơn thức R(x).
a) Sắp xếp đa thức (một biến) theo số mũ giảm dần của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần của biến.
b) Quan sát bảng để đưa ra các đơn thức thích hợp phù hợp với biến có số mũ tương ứng.
c) Xác định đơn thức R(x) dựa vào kết quả phần b).
Lời giải chi tiết:
a) \(P(x) = 5{x^2} + 4 + 2x = 5{x^2} + 2x + 4\); \(Q(x) = 8x + {x^2} + 1 = {x^2} + 8x + 1\).
b)
Đa thức | Đơn thức có số mũ 2 của biến (Đơn thức chứa \({x^2}\)) | Đơn thức có số mũ 1 của biến (Đơn thức chứa x) | Số hạng tự do (Đơn thức không chứa x) |
P(x) | \(5{x^2}\) | 2x | 4 |
Q(x) | \({x^2}\) | 8x | 1 |
R(x) | \(6{x^2}\) | 10x | 5 |
c) Vậy \(R(x) = 6{x^2} + 10x + 5\).
Đúng 0
Bình luận (0)
cách cộng 2 lũy thừa cùng số mũ khác cơ số là gì vậy mn
Cộng 2 lũy thừa cùng số mũ và khác cơ số thì không có công thức chung nào em nhé.
Đúng 0
Bình luận (0)
cách cộng lũy thừa cùng biến nhưng khác số mũ được không ạ ;-;
Có lẽ là nên tách lũy thừa ra sao cho hai phần đều có cùng số mũ xong rồi áp dụng phân tích đa thức thành nhân tử là tốt nhất
Đúng 0
Bình luận (0)
Anh ơi, em thử rồi nhưng không có kết quả . Nếu số mũ là 2 thì sao ạ?
Đúng 0
Bình luận (0)
cho 4 số tự nhiên a b c và d đều khác 0 thỏa mãn đẳng thức a mũ 2 cộng b mũ 2 bằng c mũ 2 cộng b mũ 2 chứng minh rằng a + b+c+d là 1 hợp số
x mũ ba cộng x mũa 2z cộng y mũ 2z trừ xyz cộng y mũ 3
phân tích đa thức thành nhân tử ạ
Cho tỉ lệ thức a/b=c/d với a khác 0,b khác 0,c khác 0,d khác 0,a khác cộng trừ b,c khác cộng trừ d.
Chứng Minh: (a-b/c-d)mũ 2020= a mũ 2020+b mũ 2020/ ( phần ) c mũ 2020+d mũ 2020
Xem chi tiết


















