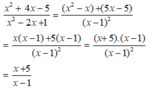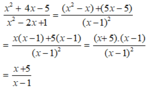Tính GTLN của biểu thức sau A = 4x - 5x2

Những câu hỏi liên quan
tìm GTNN của biểu thức A= 2x2-8x+1
Tìm GTLN của B = -5x2-4x+1
cảm ơn nha^^
a: Ta có: \(A=2x^2-8x+1\)
\(=2\left(x^2-4x+\dfrac{1}{2}\right)\)
\(=2\left(x^2-4x+4-\dfrac{7}{2}\right)\)
\(=2\left(x-2\right)^2-7\ge-7\forall x\)
Dấu '=' xảy ra khi x=2
Đúng 2
Bình luận (0)
tìm GTLN của biểu thức
C=-x2-4x-y2+8y+2
D=2023-8x+2y+4xy-y2-5x2
\(C=-\left(x^2+4x+4\right)-\left(y^2-8y+16\right)+22\\ =-\left(x^2+2x.2+2^2\right)-\left(y^2-2.y.4+4^2\right)+22\\ =-\left(x+2\right)^2-\left(y-4\right)^2+22\\ Vậy:max_C=22.khi.x=-2.và.y=4\)
Đúng 3
Bình luận (0)
Tìm GTLN của biểu thức:
K= -5x2+20x-2021
Lời giải:
$K=-5x^2+20x-2021=-2001-5(x^2-4x+4)=-2001-5(x-2)^2$
Vì $(x-2)^2\geq 0, \forall x\in\mathbb{R}$
$\Rightarrow K=-2001-5(x-2)^2\leq -2001$
Vậy $K_{\max}=-2001$ khi $(x-2)^2=0\Leftrightarrow x=2$
Đúng 1
Bình luận (0)
Ta có: \(K=-5x^2+20x-2021\)
\(=-5\left(x^2-4x+\dfrac{2021}{5}\right)\)
\(=-5\left(x^2-4x+4+\dfrac{2001}{5}\right)\)
\(=-5\left(x-2\right)^2-2001\le-2001\forall x\)
Dấu '=' xảy ra khi x=2
Đúng 0
Bình luận (0)
tìm gtln của biểu thức
P = 2 - 5x2 - y2 - 6xy + 2x
Biểu thức không có max. Bạn coi lại đề.
Đúng 1
Bình luận (0)
tìm GTLN của biểu thức
D=2023-8x+2y+4xy-y2-5x2
\(D=2023-8x+2y+4xy-y^2-5x^2\)
\(=-\left(y^2+5x^2-4xy-2y+8x-2023\right)\)
\(=-\left(y^2-2.y.\left(2x+1\right)+\left(2x+1\right)^2-\left(2x+1\right)^2+5x^2+8x-2023\right)\)
\(=-\left[\left(y-2x-1\right)^2-4x^2-4x-1+5x^2+8x-2023\right]\)
\(=-\left[\left(y-2x-1\right)^2+x^2+4x-2024\right]\)
\(=-\left[\left(y-2x-1\right)^2+\left(x+2\right)^2\right]+2028\)
Vì \(-\left[\left(y-2x-1\right)^2+\left(x+2\right)^2\right]\le0\forall x,y\)
\(MaxD=2028\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-3\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức sau:
x
2
+
4
x
-
5
x
2
-
2
x
+
1
. A.
x
-
5
x
-
1...
Đọc tiếp
Rút gọn biểu thức sau: x 2 + 4 x - 5 x 2 - 2 x + 1 .
A. x - 5 x - 1
B. x + 5 x - 1
C. x - 5 x + 1
D. x + 5 x + 1
Rút gọn biểu thức sau:
x
2
+
4
x
-
5
x
2
-
2
x
+
1
. A.
x
-
5
x
-
1
...
Đọc tiếp
Rút gọn biểu thức sau: x 2 + 4 x - 5 x 2 - 2 x + 1 .
A. x - 5 x - 1
B. x + 5 x - 1
C. x - 5 x + 1
D. x + 5 x + 1
Tìm GTLN của các biểu thức sau:
a)3-x^2+2x (GTLN)
b)4X^2-20X+40(GTLN)
Tính GTNN, GTLN của các biểu thức sau:
a)A(x,y)=4x2+y2+4x-y+1
b)B(x,y)=2x2+y2+2xy-x+5
Toán lớp 8Lớn nhất - nhỏ nhất
Tìm GTLN của biểu thức sau:
\(A=4x^2+4x+11\)
Ta có : \(A=4x^2+4x+11\)
=> \(A=4x^2+4x+1+10\)
=> \(A=\left(2x+1\right)^2+10\)
Ta thấy : \(\left(2x+1\right)^2\ge0\)
=> \(\left(2x+1\right)^2+10\ge10\)
Vậy MinA = 10 khi x = -1/2 .
Sửa đề: Tìm GTNN của biểu thức sau: \(A=4x^2+4x+11\)
Giải:
Ta có:
\(A=4x^2+4x+11=4x^2+4x+1+10=\left(2x+1\right)^2\ge10\)
Vậy \(A_{min}=10\) khi \(x=-\frac{1}{2}\)
Ta có: \(A=4x^2+4x+11\)
\(=\left(2x\right)^2+2\cdot2x\cdot1+1+10\)
\(=\left(2x+1\right)^2+10\)
Ta có: \(\left(2x+1\right)^2\ge0\forall x\)
\(\Rightarrow\left(2x+1\right)^2+10\ge10\forall x\)
Dấu '=' xảy ra khi
\(\left(2x+1\right)^2=0\Leftrightarrow2x+1=0\Leftrightarrow2x=-1\Leftrightarrow x=\frac{-1}{2}\)
Vậy: Giá trị nhỏ nhất của biểu thức \(A=4x^2+4x+11\) là 10 khi \(x=\frac{-1}{2}\)