cho hình 57, chứng minh ba điểm B,K,C thẳng hàng

Những câu hỏi liên quan
Cho hình vẽ Chứng minh ba điểm B K C thẳng hàng
Xem thêm câu trả lời
Cho hình dưới (hình 65a). Chứng minh rằng ba điểm B, K, C thẳng hàng
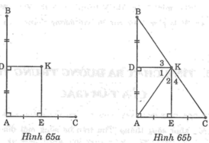
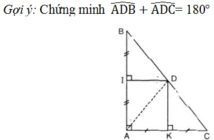
Nối KA, KB, KC (hình 65b).
Vì KD là đường trung trực của AB nên:
KA = KB (tính chất đường trung trực)
Suy ra: ΔKAB cân tại K
Do đó KD là đường phân giác của ∠(AKB)
Suy ra: ∠K1 = ∠K3 ⇒ ∠(AKB) = 2 ∠K1 (1)
Vì KE là đường trung trực của AC nên:
KA = KC (tính chất đường trung trực)
Do đó, tam giác AKC cân tại K. Suy ra KE là đường phân giác của ∠(AKC)
Suy ra: ∠K2 = ∠K4 ⇒ ∠(AKC) = 2 ∠K2 (2)
Ta có: KD ⊥ AB (gt) và AC ⊥ AB (gt)
Suy ra: KD // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song nhau)
Lại có: KE ⊥ AC (gt)
Suy ra: KE ⊥ KD (quan hệ giữa tính vuông góc và tính song song)
Hay: ∠(DKE) = 90o⇒ ∠K1 +∠K2 = 90o
Từ (1) và (2) suy ra: ∠(AKB) + ∠(AKC) = 2∠K1 + 2∠K2
= 2.( ∠K1 +∠K2 ) = 2.90o = 180o.
Vậy B, K, C thẳng hàng.
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB//CD) gọi E , F , K lần lượt là trung điểm của Ad , AC , BC a) Chứng minh EF//CD b) Chứng minh EK//CD c) Chứng minh ba điểm E,F,K thẳng hàng
Cho hình 51: Chứng minh ba điểm B, C, D thẳng hàng.
Hình 51
QUẢNG CÁOTừ hình vẽ ta có:
+ DK là đường trung trực của AC ⇒ DA = DC.
+ DI là đường trung trực của AB ⇒ DA = DB.
+ Ta có : DI // AC (vì cùng ⏊ AB)
Mà DK ⏊ AC ⇒ DK ⏊ DI 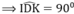
+ Xét ∆ADK và ∆CDK có:
AD = DC
AK = CK (gt)
DK chung
⇒ ∆ADK = ∆CDK (c.c.c)
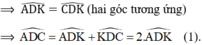
+ Xét ∆ADI và ∆BDI có :
AD = BD
AI = BI (gt)
DI chung
⇒ ∆ADI = ∆BDI (c.c.c)
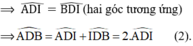
Từ (1) và (2) suy ra
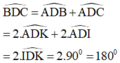
Vậy B, D, C thẳng hàng.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M và N lần lượt là trung điểm của AB và SC. a) Xác định giao điểm I, K của đường thẳng AN,MN với (SBD); b) Chứng minh ba điểm B,I,K thẳng hàng c) Xác định thiết diện của hình chóp S.ABCD khi cắt bởi (ABN); d) Tính các tỷ số (IA)/(IN), (KM)/(KN), (IB)/(IK)
a: Gọi O là giao điểm của AC và BD
Chọn mp(SAC) có chứa AN
\(O\in AC\subset\left(SAC\right);O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Gọi I là giao điểm của SO với AN
=>I là giao điểm của AN với mp(SBD)
Chọn mp(AMN) có chứa MN
\(B\in AM\subset\left(AMN\right)\)
\(B\in BD\subset\left(SBD\right)\)
Do đó: \(B\in\left(AMN\right)\cap\left(SBD\right)\)
mà \(I\in\left(AMN\right)\cap\left(SBD\right)\)
nên (AMN) giao (SBD)=BI
Gọi K là giao điểm của BI với MN
=>K là giao điểm của MN với mp(SBD)
b: K là giao điểm của BI với MN
=>B,I,K thẳng hàng
d: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm của AC và O là trung điểm của BD
Xét ΔSAC có
O,N lần lượt là trung điểm của CA,CS
=>ON là đường trung bình
=>ON//SA và ON=SA/2
Xét ΔINO và ΔIAS có
\(\widehat{INO}=\widehat{IAS}\)
\(\widehat{NIO}=\widehat{AIS}\)
Do đó: ΔINO đồng dạng với ΔIAS
=>\(\dfrac{IN}{IA}=\dfrac{NO}{AS}=\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
Cho ΔMNP, H là trung điểm của NP. Trên tia đối của HM lấy điểm K sao cho HK=HM a, Chứng minh ΔMHP= ΔKHN b, Chứng minh MP//NK c, Gọi X là một điểm trên MP, Y là một điểm trên NK sao cho MX=KY. Chứng minh ba điểm X, H, Y thẳng hàng (có hình)
b: Xét tứ giác NMPK có
H là trung điểm của NP
H là trung điểm của MK
Do đó: NMPK là hình bình hành
Suy ra: MP//NK
Đúng 0
Bình luận (0)
Cho hai hình vuông ABCD và DEFG, trong đó các bộ ba điểm A, D, G và D, C, E sắp xếp theo thứ tự thẳng hàng. Trên tia AD lấy điểm H sao cho AHDG, trên tia CE lấy điểm K sao cho CKDG.a) Chứng minh bốn tam giác ABH, HGF, FEK, BCK bằng nhau.b) Chứng minh BHFK là hình vuông.c) Gọi J là tâm đối xứng của hình vuông BHFK. Chứng minh ba điểm A, C, J thẳng hàng. d) Chứng minh ba đường thẳng AC, GE, HK đồng qui.
Đọc tiếp
Cho hai hình vuông ABCD và DEFG, trong đó các bộ ba điểm A, D, G và D, C, E sắp xếp theo thứ tự thẳng hàng. Trên tia AD lấy điểm H sao cho AH=DG, trên tia CE lấy điểm K sao cho CK=DG.
a) Chứng minh bốn tam giác ABH, HGF, FEK, BCK bằng nhau.
b) Chứng minh BHFK là hình vuông.
c) Gọi J là tâm đối xứng của hình vuông BHFK. Chứng minh ba điểm A, C, J thẳng hàng.
d) Chứng minh ba đường thẳng AC, GE, HK đồng qui.
Cho hình 13.
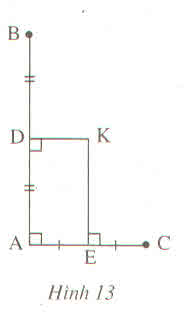
Chứng minh rằng ba điểm B, K, C thẳng hàng ?
Nối KA,KB,KC.
Ta có KD là đường trung trực AB
=>KA=KB(tính chất đường trung trực)
\(\Rightarrow\Delta KAB\) cân tại K nên KD là đường phân giác của \(\widehat{AKB}\)
\(\Rightarrow\widehat{K_1}=\widehat{K_3}\)
\(\Rightarrow\widehat{AKB}=2\widehat{K_1}\) (1)
KE là đường trung trực của AC
=>KA=KC(tính chất đường trung trực)
\(\Rightarrow\Delta KAC\) cân tại K nên KE là đường phân giác của \(\widehat{AKC}\)
\(\Rightarrow\widehat{K_2}=\widehat{K_4}\)
\(\Rightarrow\widehat{AKC}=2\widehat{K_2}\left(2\right)\)
\(KD\perp AB\left(gt\right)\)
\(AC\perp AB\left(gt\right)\)
Cho hình bình hành ABCD. Gọi H và K lần lượt là hình chiếu của A và C trên đường chéo BD.
a)v Chứng minh rằng DH = BK
b) Chứng minh rằng tứ giác AHCK là hình bình hành
c) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng.
nhanh 3 k miễn phí mai nhớ cổ vũ đội bóng việt nam nha
Đúng 0
Bình luận (0)
b) Xét hai tam giác vuông AHD và CKB có:
AD=BC
góc ADB=góc DBC (so le trong).
=> tam giác AHD=tam giác CKB (ch-gn)
=> BH=CK( hai cạnh tương ứng)
Lấy M trung điểm BD , nên MD=MB => MD-DH=MB-BK=> MH=MK, nên M Trung điểm HK
Vì ABCD là hình bình hành nên AC cắt BD tại trung điểm M.
Hay M là Trung điểm AC, mà M trung điểm HK.
Nên AKCH là hình bình hành.
Đúng 0
Bình luận (0)
c) AHCK là HBH =>2 đường chéo AC và HK cắt nhau tại trung điểm của mỗi đường
Mà O là trung điểm của HK
=> O là trung điể của AC
=> A,O,C thẳng hàng
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình bình hành ABCD. Gọi H và K là hình chiếu của A và C trên đường chéo BD ( H,K thuộc BD). Điểm O là trung điểm của đoạn thẳng HK.
a) chứng minh : tứ giác AHKC là hình bình hành
b) chứng minh: ba điểm A,O,C thẳng hàng
c) Gọi M là giao điẻm của KC và AB , N là giao điểm của AH và CD . Chứng minh AC,BD,MN đồng quy





















