Nhắc lại định nghĩa :
a) Góc giữa đường thẳng và mặt phẳng
b) Góc giữa hai mặt phẳng
Nhắc lại định nghĩa:
a) Góc giữa đường thẳng và mặt phẳng.
b) Góc giữa hai mặt phẳng.
a) Định nghĩa: Góc giữa đường thẳng và mặt phẳng.
Cho đường thẳng d cắt mặt phẳng (α) tại điểm O và d không vuông góc với (α). Góc giữa đường thẳng d và mặt phẳng (α) là góc tạo bởi đường thẳng d và hình chiếu vuông góc góc d' của d trên mặt phẳng (α), kí hiệu góc (d,α).
- Nếu d vuông góc góc với (α) ta qui ước góc (d,α) = 90o.
- Nếu d // (α) hay d nằm trong (α) ta quy ước góc (d,α) = 90o.
b) Định nghĩa: Góc giữa hai mặt phẳng
Giả sử hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến c. Từ điểm I bất kì trên c ta dựng trong (α) đường thẳng a vuông góc với c và dựng trong (β) đường thẳng b vuông góc với c. Ta gọi góc giữa hai đường a và b là góc giữa hai mặt phẳng (α) và (β). Như vậy góc giữa hai mặt phẳng (α) và (β) luôn có số đo bé hơn hoặc bằng 90o.
*Nếu hai mặt phẳng song song hoặc trùng với nhau thì ta nói rằng góc giữa hai mặt phẳng đó bằng 0o. Góc giữa hai mặt phẳng (α) và (β) được kí hiệu là (α, β), ta có 0o ≤ (α, β) ≤ 90o.
Cho các phát biểu sau về góc giữa hai mặt phẳng cắt nhau:
Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng tương ứng vuông góc với hai mặt phẳng đó (I)
Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng tương ứng song song với hai mặt phẳng đó (II)
Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng cùng vuông góc với giao tuyến của hai mặt phẳng đó (III)
Trong các phát biểu trên có bao nhiêu phát biểu là Đúng?
A. 2
B. 1
C. 3
D. 0
Cho các phát biểu sau về góc giữa hai mặt phẳng cắt nhau:
Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng tương ứng vuông góc với hai mặt phẳng đó (I)
Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng tương ứng song song với hai mặt phẳng đó (II)
Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng cùng vuông góc với giao tuyến của hai mặt phẳng đó (III)
Trong các phát biểu trên có bao nhiêu phát biểu là Đúng?
A. 2
B. 1
C. 3
D. 0
Cho mặt phẳng (P) chứa đường thẳng b vuông góc với mặt phẳng (Q). Lấy một đường thẳng a vuông góc với (P) (H.7.47).
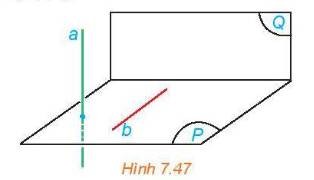
a) Tính góc giữa a và b.
b) Tính góc giữa (P) và (Q).
a) \(\left. \begin{array}{l}a \bot \left( P \right)\\b \subset \left( P \right)\end{array} \right\} \Rightarrow a \bot b \Rightarrow \left( {a,b} \right) = {90^0}\)
b) Gọi \(\left( P \right) \cap \left( Q \right) = \Delta \)
\(\begin{array}{l}a \bot \Delta \left( {a \bot \left( P \right)} \right)\\b \bot \Delta \left( {b \bot \left( Q \right)} \right)\\ \Rightarrow \left( {\left( P \right),\left( Q \right)} \right) = \left( {a,b} \right) = {90^0}\end{array}\)
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a có cạnh SA=a căn 2 và SA vuông góc với mặt phẳng với (ABCD).Tính a) Góc giữa đường thẳng BC và mặt phẳng (SAB) b)Góc giữa đường thẳng DC và mặt phẳng (SAB)
Trong mặt phẳng cho hai đường thẳng a, b.
a) Nếu a và b cắt nhau tại O (Hình 2) thì góc giữa hai đường thẳng a, b được xác định như thế nào?
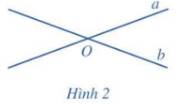
b) Nếu a // b thì góc giữa a và b bằng bao nhiêu độ?
c) Nếu a và b trùng nhau thì góc giữa a và b bằng bao nhiêu độ?
a) Nếu a và b cắt nhau tại O thì: \(0^\circ \le \left( {a,b} \right) \le 90^\circ \)
b) Nếu a // b thì không có góc tạo bởi a và b
c) Nếu a và b trùng nhau thì góc giữa a và b bằng \(0^\circ \)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng 60 0 . Tính theo a khoảng cách giữa 2 đường thẳng SB,AD?
A. a 3
B. a 3 2
C. a 3 3
D. a 3 5
Đáp án B
Hướng dẫn giải:
+)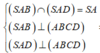
![]()
![]()
+) ![]()
![]()
+) Ta có A B ⊥ B C , kẻ A P ⊥ S B ( P ∈ S B )
d(A;(SBC)) = AP ⇒ d(AD;SB) = AP
+) 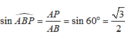
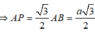
![]()
Cho hai đường thẳng ∆ và ∆ ′ chéo nhau nhận AA’ làm đoạn vuông góc chung, trong đó A thuộc ∆ và A’ thuộc ∆ ′ . Gọi (P) là mặt phẳng qua A vuông góc với ∆ ′ và d là hình chiếu vuông góc của ∆ trên mặt phẳng (P). Đặt AA’ = a, góc nhọn giữa ∆ và d là α . Mặt phẳng (Q) song song với mặt phẳng (P) cắt ∆ và ∆ ′ lần lượt tại M và M’. Gọi M 1 là hình chiếu vuông góc của M lên mặt phẳng (P).
Chứng minh 5 điểm A, A’, M, M’, M 1 cùng nằm trên mặt cầu (S). xác định tâm O của (S). Tính bán kính của (S) theo a, α và khoảng cách x giữa hai mặt phẳng (P) và (Q).
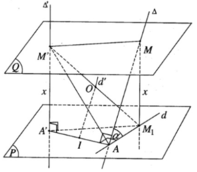
Vì mặt phẳng (P) qua A và vuông góc với Δ′ nên AA’ thuộc (P). Vì M thuộc ∆ mà d là hình chiếu vuông góc của ∆ trên (P) nên M 1 thuộc d. Vì MA ⊥ AA′ ⇒ M 1 A ⊥ AA′
Mặt khác M 1 A ⊥ M′A′ nên ta suy ra M 1 A ⊥ (AA′M′). Do đó M 1 A ⊥ M′A và điểm A thuộc mặt cầu đường kính M’ M 1
Ta có M′A′ ⊥ (P) nên M′A′ ⊥ A′ M 1 , ta suy ra điểm A’ cũng thuộc mặt cầu đường kính M’ M 1
Ta có (Q) // (P) nên ta suy ra
M M 1 ⊥ (Q) mà MM’ thuộc (Q), do đó M 1 M ⊥ MM′
Như vậy 5 điểm A, A’, M, M’, M 1 cùng thuộc mặt cầu (S) có đường kính M’ M 1 . Tâm O của mặt cầu (S) là trung điểm của đoạn M’ M 1
Ta có M ' M 1 2 = M ' A ' 2 + A ' M 1 2 = M ' A ' 2 + A ' A 2 + AM 1 2 = x 2 + a 2 + x 2 cot 2 α vì M M 1 = x
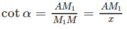
Bán kính r của mặt cầu (S) bằng (M′ M 1 )/2 nên
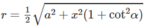
Cho hình lăng trụ ABC.A'B'C' có dayd là tam giác đều cạnh a, hình chiếu vuông góc của B' lên mặt phẳng đáy trùng với trung điểm H của cạnh AB, góc giữa mặt phẳng (BCC'B') và mặt phẳng đáy là 60°. Tính khoảng cách giữa hai đường thẳng AA' và BC
Gọi D là trung điểm BC \(\Rightarrow\left\{{}\begin{matrix}AD\perp BC\\AD=\dfrac{a\sqrt{3}}{2}\end{matrix}\right.\)
Gọi E là trung điểm BD \(\Rightarrow\) HE là đường trung bình tam giác ABD
\(\Rightarrow\left\{{}\begin{matrix}HE||AD\Rightarrow HE\perp BC\\HE=\dfrac{1}{2}AD=\dfrac{a\sqrt{3}}{4}\end{matrix}\right.\)
Mà \(B'H\perp\left(ABC\right)\Rightarrow B'H\perp BC\Rightarrow BC\perp\left(B'HE\right)\)
\(\Rightarrow\widehat{B'EH}\) là góc giữa (BCC'B') và đáy
\(\Rightarrow\widehat{B'HE}=60^0\)
\(\Rightarrow B'H=HE.tan60^0=\dfrac{3a}{4}\)
\(AA'||BB'\Rightarrow AA'||\left(BCC'B'\right)\Rightarrow d\left(AA';BC\right)=d\left(AA';\left(BCC'B'\right)\right)=d\left(A;\left(BCC'B'\right)\right)\)
Mà H là trung điểm AB \(\Rightarrow AB=2HB\Rightarrow d\left(A;\left(BCC'B'\right)\right)=2d\left(H;\left(BCC'B'\right)\right)\)
Từ H kẻ \(HK\perp B'E\)
Do \(BC\perp\left(B'HE\right)\Rightarrow\left(BCC'B'\right)\perp\left(B'HE\right)\)
Mà B'E là giao tuyến (B'HE) và (BCC'B')
\(\Rightarrow HK\perp\left(BCC'B'\right)\Rightarrow HK=d\left(H;\left(BCC'B'\right)\right)\)
Hệ thức lượng:
\(\dfrac{1}{HK^2}=\dfrac{1}{B'H^2}+\dfrac{1}{HE^2}\Rightarrow HK=\dfrac{B'H.HE}{\sqrt{B'H^2+HE^2}}=\dfrac{3a}{8}\)
\(\Rightarrow d\left(AA';BC\right)=2HK=\dfrac{3a}{4}\)