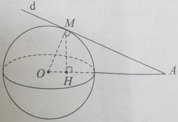
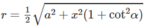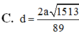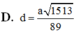Cho hai đường thẳng ∆ và ∆ ′ chéo nhau nhận AA’ làm đoạn vuông góc chung, trong đó A thuộc ∆ và A’ thuộc ∆ ′ . Gọi (P) là mặt phẳng qua A vuông góc với ∆ ′ và d là hình chiếu vuông góc của ∆ trên mặt phẳng (P). Đặt AA’ = a, góc nhọn giữa ∆ và d là α . Mặt phẳng (Q) song song với mặt phẳng (P) cắt ∆ và ∆ ′ lần lượt tại M và M’. Gọi M 1 là hình chiếu vuông góc của M lên mặt phẳng (P).
Chứng minh 5 điểm A, A’, M, M’, M 1 cùng nằm trên mặt cầu (S). xác định tâm O của (S). Tính bán kính của (S) theo a, α và khoảng cách x giữa hai mặt phẳng (P) và (Q).
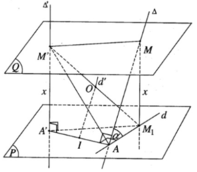
Vì mặt phẳng (P) qua A và vuông góc với Δ′ nên AA’ thuộc (P). Vì M thuộc ∆ mà d là hình chiếu vuông góc của ∆ trên (P) nên M 1 thuộc d. Vì MA ⊥ AA′ ⇒ M 1 A ⊥ AA′
Mặt khác M 1 A ⊥ M′A′ nên ta suy ra M 1 A ⊥ (AA′M′). Do đó M 1 A ⊥ M′A và điểm A thuộc mặt cầu đường kính M’ M 1
Ta có M′A′ ⊥ (P) nên M′A′ ⊥ A′ M 1 , ta suy ra điểm A’ cũng thuộc mặt cầu đường kính M’ M 1
Ta có (Q) // (P) nên ta suy ra
M M 1 ⊥ (Q) mà MM’ thuộc (Q), do đó M 1 M ⊥ MM′
Như vậy 5 điểm A, A’, M, M’, M 1 cùng thuộc mặt cầu (S) có đường kính M’ M 1 . Tâm O của mặt cầu (S) là trung điểm của đoạn M’ M 1
Ta có M ' M 1 2 = M ' A ' 2 + A ' M 1 2 = M ' A ' 2 + A ' A 2 + AM 1 2 = x 2 + a 2 + x 2 cot 2 α vì M M 1 = x
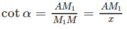
Bán kính r của mặt cầu (S) bằng (M′ M 1 )/2 nên