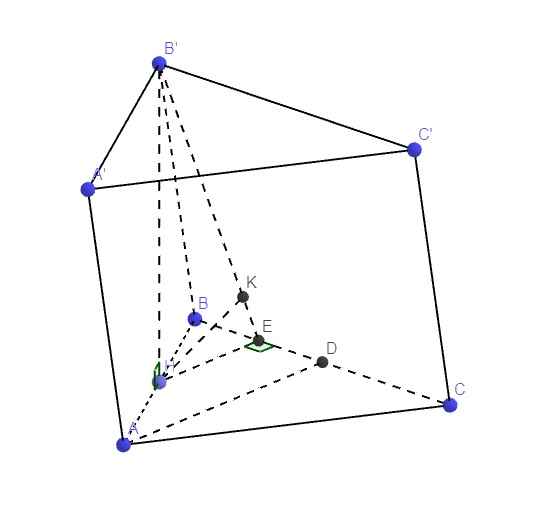
Gọi D là trung điểm BC \(\Rightarrow\left\{{}\begin{matrix}AD\perp BC\\AD=\dfrac{a\sqrt{3}}{2}\end{matrix}\right.\)
Gọi E là trung điểm BD \(\Rightarrow\) HE là đường trung bình tam giác ABD
\(\Rightarrow\left\{{}\begin{matrix}HE||AD\Rightarrow HE\perp BC\\HE=\dfrac{1}{2}AD=\dfrac{a\sqrt{3}}{4}\end{matrix}\right.\)
Mà \(B'H\perp\left(ABC\right)\Rightarrow B'H\perp BC\Rightarrow BC\perp\left(B'HE\right)\)
\(\Rightarrow\widehat{B'EH}\) là góc giữa (BCC'B') và đáy
\(\Rightarrow\widehat{B'HE}=60^0\)
\(\Rightarrow B'H=HE.tan60^0=\dfrac{3a}{4}\)
\(AA'||BB'\Rightarrow AA'||\left(BCC'B'\right)\Rightarrow d\left(AA';BC\right)=d\left(AA';\left(BCC'B'\right)\right)=d\left(A;\left(BCC'B'\right)\right)\)
Mà H là trung điểm AB \(\Rightarrow AB=2HB\Rightarrow d\left(A;\left(BCC'B'\right)\right)=2d\left(H;\left(BCC'B'\right)\right)\)
Từ H kẻ \(HK\perp B'E\)
Do \(BC\perp\left(B'HE\right)\Rightarrow\left(BCC'B'\right)\perp\left(B'HE\right)\)
Mà B'E là giao tuyến (B'HE) và (BCC'B')
\(\Rightarrow HK\perp\left(BCC'B'\right)\Rightarrow HK=d\left(H;\left(BCC'B'\right)\right)\)
Hệ thức lượng:
\(\dfrac{1}{HK^2}=\dfrac{1}{B'H^2}+\dfrac{1}{HE^2}\Rightarrow HK=\dfrac{B'H.HE}{\sqrt{B'H^2+HE^2}}=\dfrac{3a}{8}\)
\(\Rightarrow d\left(AA';BC\right)=2HK=\dfrac{3a}{4}\)