Cho \(\Delta MNP\) có I nằm giữa MP
CMR: \(NI< \dfrac{MN+NP+PM}{2}\)
Bài 3: Cho tam giác MNP có MN = 4cm, MP = 6cm, NP = 8cm. Kéo dài MN lấy điểm I sao cho NI = NM, kéo dài MP lấy điểm K sao cho PK = PM, kéo dài trung tuyến MO của tam giác MNP lấy OS = OM.
1) Tính độ dài các cạnh của tam giác MIK.
2) Chứng minh ba điểm I, S, K thẳng hàng.
3) Chứng minh SMKI = 4SMNP( giải giúp mình câu 3 vs ạ mình cần gấp)
Câu 3: Cho ΔMNP có MN=15cm, MP=20cm, NP=25cm
a) Chứng minh ; ΔMNP là tam giác vuông
b)Gọi I là trung điểm của cạnh MP. Tính độ dài đoạn thẳng NI
Cho tam giác MNP cân tại P có PM = PN = 15 cm, MN = 18cm. Kẻ PI ⊥ MN (I ϵ MN). Kẻ IH ⊥ MP (H ϵ MP), IK ⊥ NP (K ϵ NP)
a) Chứng minh rằng ΔMIP = ΔNIP
b) Chứng minh rằng IH = IK
c) Tính độ dài IP
d) Chứng minh HK // AB
e) Gọi O là giao điểm của IP và HK. Chứng minh \(\widehat{MON}\) = 180o + \(\widehat{PMO}+\widehat{PNO}+\widehat{HIK}\)
cho \(\Delta\)MNP, góc M =90 độ đg cao MI . tính MN,MP,NP,NI
Cho \(\Delta MNP\)có \(MN=MP\). I là trung điểm của NP
a) CMR \(\Delta MNI=\Delta MPI\)(Câu này mình bt rồi)
b) CMR MI\(\perp\)NP (câu này cx bt nha)
c) Kẻ NK\(\perp\)MP, CH\(\perp\)MN Gọi giao điểm chỏ NK và CH là T. CMR MTI thẳng hàng
a/ Xét tam giác MNI và tam giác MPI có:
\(\hept{\begin{cases}MN=MP\left(gt\right)\\NI=IP\left(gt\right)\\MI:canhchung\end{cases}}\)
suy ra tam giác MNI = tam giác MPI
Vậy : ....... ( đpcm )
Nhớ k cho mình nhé! Thank you!!!
Bài 1: Cho tam giác MNP có MN=4cm, MP=6cm, NP=8cm. Kéo dài MN lấy điểm I sao cho NI=NM kéo dài MP lấy điểm K sao cho PK=PM, kéo dài đường trung tuyến MO của tam giác MNP lấy OS=OM.
1) Tính độ dài các cạnh của tam giác MIK
2) Chứng mjnh ba điểm I,S,K thẳng hàng
3) Chứng minh SMKI=4SMNP
Bài 2) Cho tam giác ABC cân tại A có M là trung điểm của đường cao AH, CM cắt AB tại D, kẻ Hx//CD và cắt AB tại E. CMR:
1) DA=DE
2) AB=3AD
3) CD=4MD
Cho tam giác MNP có MN = 4cm, MP= 6cm, NP =8cm.Kéo dài MN lấy I sao cho IN =NM , Kéo dài MP lấy K sao cho PK=PM, kéo dài đường trung tuyến MO của tam giác MNP lấy OS=OM.Chứng minh S tam giác MKI = 4.S tam giác MNP
Cho tam giác MNP vuông tại M có MN=4cmc ,NP=5cm.Trên tia đối của tia MN lấy điểm A sao cho MN=MA.
a) Chứng minh PN=PA.
b) Gọi B là trung điểm cua AP,đường thẳng NB cắt PM tại G.Tính MP;GP.
c) Đường trung trực của đoạn thẳng MP cắt MP tại I và cắt NP tại C.Chứng minh ba đường thẳng PM,NB và AC đồng quy.
d) Chứng minh IA+IP<NA+NP.
a: Xét ΔPAN có
PM vừa là đường cao, vừa là trung tuyến
=>ΔPAN cân tại P
b: \(PM=\sqrt{5^2-4^2}=3\left(cm\right)\)
Xét ΔPAN có
NB,PM là trung tuyến
NB cắt PM tại G
=>G là trọng tâm
GP=2/3*3=2cm
c: CI là trung trực của MP
=>I là trung điểm của MP và CI vuông góc MP tại I
Xét ΔMPN có
I là trung điểm của PM
IC//MN
=>C là trung điểm của PN
=>PM,NB,AC đồng quy
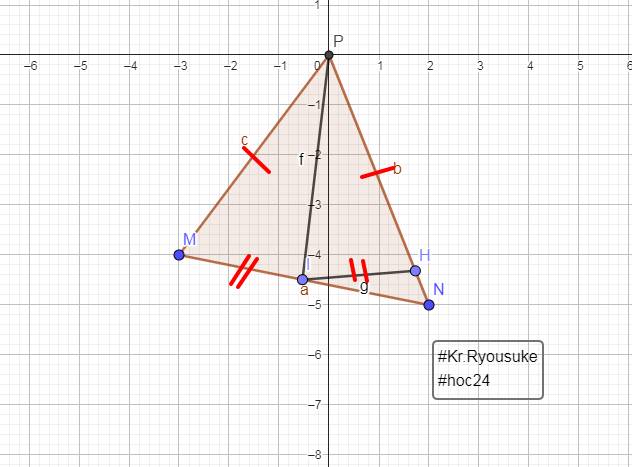
Cho tam giác MNP (MP< NP)đường phân giác PI của góc MPN (I thuộc MN ). Trên cạnh NP của tam giác MNP lấy điểm H sao cho PH=PM. Chứng minh rằng IM=IH
Xét `\Delta PMI` và `\Delta PHI`:
`\text {PH = PM (gt)}`
$\widehat {MPI} = \widehat {HPI} (\text {tia phân giác} \widehat {MPN}$
`\text { PI chung}`
`=> \Delta PMI = \Delta PHI (c-g-c)`
`-> \text {IM = IH (2 cạnh tương ứng)}`