Giúp em câu b và c với ạ, em cần gấp

 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB, ta được:
\(AM\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC, ta được:
\(AN\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
Giải giúp em câu b với c ạ. E cần gấp 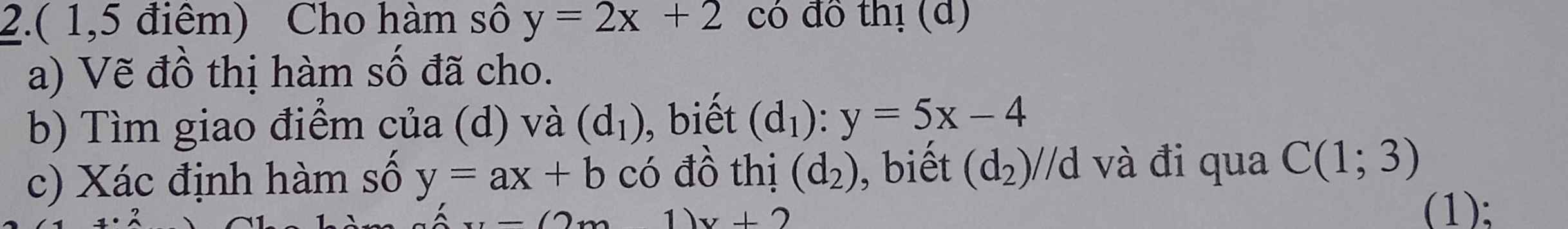
b: Tọa độ giao là:
5x-4=2x+2 và y=2x+2
=>x=2 và y=6
c: Vì (d2)//d nên (d2): y=2x+b
Thay x=1 và y=3 vào (d2), ta được:
b+2=3
=>b=1
em cần gấp câu b và c ạ, nhờ mn giúp
a: Thay x=25 vào A, ta được:
\(A=\dfrac{5-1}{5+1}=\dfrac{4}{6}=\dfrac{2}{3}\)
b: \(B=\dfrac{x-\sqrt{x}-x-2\sqrt{x}-1-2\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-5\sqrt{x}-5}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{-5}{\sqrt{x}-1}\)
c: \(P=AB=\dfrac{-5}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{-5}{\sqrt{x}+1}\)
Để P<-1 thì P+1<0
\(\Rightarrow-5+\sqrt{x}+1< 0\)
\(\Leftrightarrow\sqrt{x}< 4\)
=>x<16
mà x là số nguyên lớn nhất
nên x=15
Giúp em với và cảm ơn ạ. Em cần giúp câu b, c, d ạ

Giúp em câu c với ạ em đang cần gấp!!!!!!!
d.
Theo chứng minh câu c ta có tam giác NPO cân tại N
Mà I là trung điểm OP \(\Rightarrow NI\) là đường trung tuyến
Trong tam giác NPO cân tại N, NI là trung tuyến nên nó đồng thời là phân giác góc \(\widehat{ONP}\)
Hay NI là phân giác trong góc \(\widehat{MNP}\)
Lại có ND cũng là phân giác trong góc \(\widehat{MNP}\) (giả thiết)
\(\Rightarrow\) Đường thẳng NI trùng đường thẳng ND
Hay 3 điểm N, D, I thẳng hàng

mọi người làm giúp em câu c với ạ
em đang cần gấp ạ
MN là đường trung bình tam giác SAB \(\Rightarrow\) MN song song và bằng 1 nửa AB
Gọi P là trung điểm AD \(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow P\in\left(MNQ\right)\)
\(\Rightarrow\) MNQP là thiết diện của chóp và (MNQ)
Do MN song song PQ \(\Rightarrow\) MNQP là hình thang
Lại có M, P là trung điểm SA, AD \(\Rightarrow MP=\dfrac{1}{2}SD\)
Tương tự \(NQ=\dfrac{1}{2}SC\Rightarrow MP=NQ=\dfrac{b\sqrt{3}}{2}\)
\(\Rightarrow\) Thiết diện là hình thang cân
\(PQ=AB=a\) ; \(MN=\dfrac{1}{2}PQ=\dfrac{a}{2}\)
Kẻ \(MH\perp PQ\Rightarrow PH=\dfrac{PQ-MN}{2}=\dfrac{a}{4}\)
\(\Rightarrow MH=\sqrt{MP^2-PH^2}=\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
\(S=\dfrac{1}{2}\left(MN+PQ\right).MH=\dfrac{3a}{4}.\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
Giúp em câu 35 và 38 với ạ em cần gấp 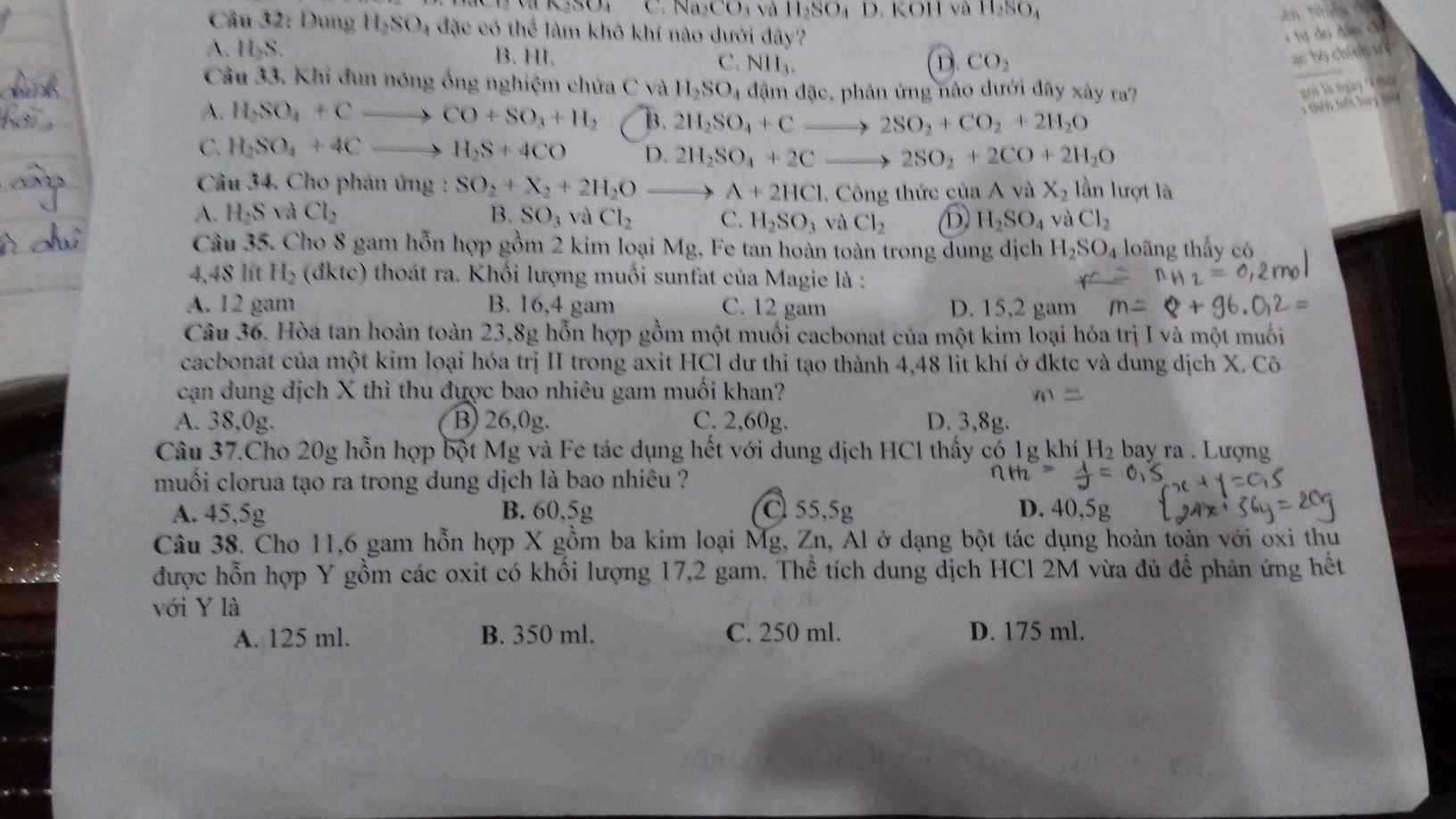
Mn giúp em câu b,c,d ạ, em cần gấp ạ
a) Thay \(x=\dfrac{1}{4}\) vào Q, ta được:
\(Q=\dfrac{1}{\dfrac{1}{4}\cdot\dfrac{1}{2}+27}=\dfrac{1}{27+\dfrac{1}{8}}=\dfrac{8}{217}\)
b) Ta có: \(P=\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}-\dfrac{1}{2-\sqrt{x}}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(=\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-9+\sqrt{x}+3-x+2\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}\)
c) Để \(P>\dfrac{1}{2}\) thì \(P-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{6-\left(\sqrt{x}+3\right)}{2\left(\sqrt{x}+3\right)}>0\)
\(\Leftrightarrow3-\sqrt{x}>0\)
\(\Leftrightarrow x< 9\)
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 9\\x\ne4\end{matrix}\right.\)
Mn giúp em câu b,d với ạ. Em cần gấp
a) Thay x=36 vào B, ta được:
\(B=\dfrac{6}{6-3}=\dfrac{6}{3}=2\)
b) Để \(B< \dfrac{1}{2}\) thì \(B-\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}+3}{2\left(\sqrt{x}-3\right)}< 0\)
\(\Leftrightarrow\dfrac{\sqrt{x}+3}{2\left(\sqrt{x}-3\right)}< 0\)
\(\Leftrightarrow\sqrt{x}-3< 0\)
\(\Leftrightarrow x< 9\)
Kết hợp ĐKXĐ, ta được: \(0\le x< 9\)
c) Ta có: \(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
d) Ta có: P=AB
nên \(P=\dfrac{\sqrt{x}+2}{\sqrt{x}}\cdot\dfrac{\sqrt{x}}{\sqrt{x}-3}=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
Để P nguyên thì \(\sqrt{x}+2⋮\sqrt{x}-3\)
\(\Leftrightarrow5⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3=-1\)(Vì x nhỏ nhất)
\(\Leftrightarrow\sqrt{x}=2\)
hay x=4