a) Thay x=36 vào B, ta được:
\(B=\dfrac{6}{6-3}=\dfrac{6}{3}=2\)
b) Để \(B< \dfrac{1}{2}\) thì \(B-\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}+3}{2\left(\sqrt{x}-3\right)}< 0\)
\(\Leftrightarrow\dfrac{\sqrt{x}+3}{2\left(\sqrt{x}-3\right)}< 0\)
\(\Leftrightarrow\sqrt{x}-3< 0\)
\(\Leftrightarrow x< 9\)
Kết hợp ĐKXĐ, ta được: \(0\le x< 9\)
c) Ta có: \(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
d) Ta có: P=AB
nên \(P=\dfrac{\sqrt{x}+2}{\sqrt{x}}\cdot\dfrac{\sqrt{x}}{\sqrt{x}-3}=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
Để P nguyên thì \(\sqrt{x}+2⋮\sqrt{x}-3\)
\(\Leftrightarrow5⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3=-1\)(Vì x nhỏ nhất)
\(\Leftrightarrow\sqrt{x}=2\)
hay x=4





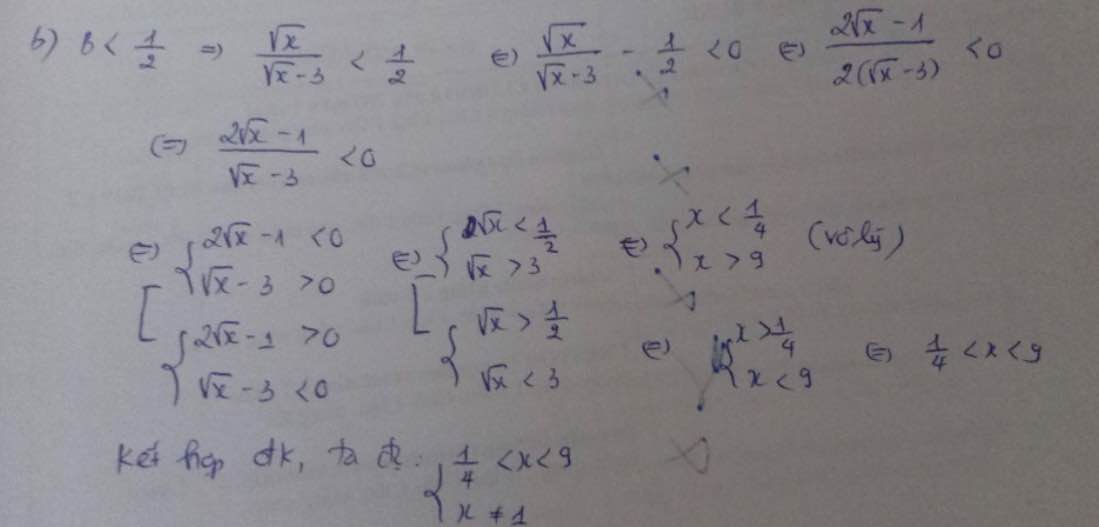
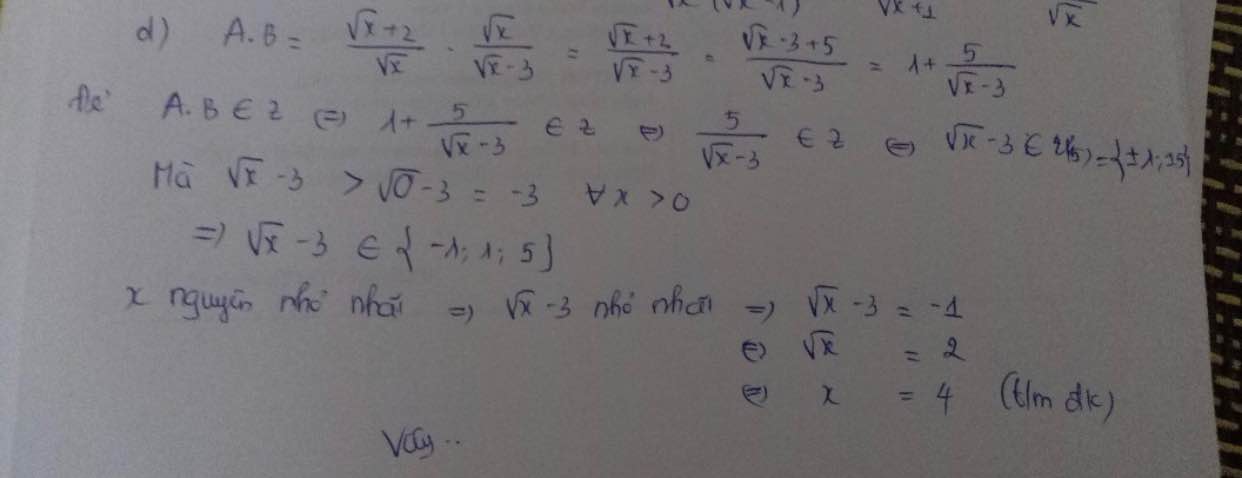


 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp