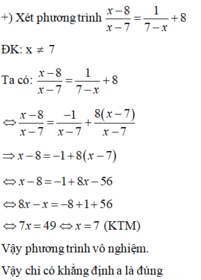Tổng các nghiệm của phương trình:
(x2 + 4x - 1)2 - 3(x2 + 4x) - 1 = 0 là

Những câu hỏi liên quan
Cho phương trình (1+4x-x2).52x^2-3x-1 + (2x2-3x-1).51+4x-x^2 = x2+x. Tổng tất cả các nghiệm của phương trình nằm trong khoảng nào dưới đây?
A.(0;4)
B. (4;6)
C.(6;8)
D. (8;12)
Cho phương trình 3
x
2
- 4x + m 0. Giá trị m để phương trình có các nghiệm
x
1
,
x
2
thỏa mãn
x
1
-
x
2
1 là: A. m -7/12 B. m 7/12 C. m 1 D. m 1/3
Đọc tiếp
Cho phương trình 3 x 2 - 4x + m = 0. Giá trị m để phương trình có các nghiệm x 1 , x 2 thỏa mãn x 1 - x 2 = 1 là:
A. m = -7/12
B. m = 7/12
C. m = 1
D. m = 1/3
Tổng các nghiệm của phương trình x 2 - 2 x + 1 = 4 x 2 - 4 x + 1 là:
A. 2 3
B. 1
C. 2
D. 3
Trong các khẳng định sau, số khẳng định đúng là:a) Tập nghiệm của phương trình
x
2
+
3
x
x
0
là {0; 3}b) Tập nghiệm của phương trình
x
2
-
4
x
-
2...
Đọc tiếp
Trong các khẳng định sau, số khẳng định đúng là:
a) Tập nghiệm của phương trình x 2 + 3 x x = 0 là {0; 3}
b) Tập nghiệm của phương trình x 2 - 4 x - 2 = 0 là {-2}
c) Tập nghiệm của phương trình x - 8 x - 7 = 1 7 - x + 8 là {0}
A. 1
B. 2
C. 0
D. 3
Giải phương trình
x
2
-
3
x
+
6
x
2
-
9
1
x
-
3
Bằng cách điền vào các chỗ trống (…) và trả lời các câu hỏi.- Điều kiện: x ≠ …- Khử mẫu và bi...
Đọc tiếp
Giải phương trình
x 2 - 3 x + 6 x 2 - 9 = 1 x - 3
Bằng cách điền vào các chỗ trống (…) và trả lời các câu hỏi.
- Điều kiện: x ≠ …
- Khử mẫu và biến đổi, ta được: x2 – 3x + 6 = … ⇔ x2 – 4x + 3 = 0.
- Nghiệm của phương trình x2 – 4x + 3 = 0 là: x1 = …; x2 = …
Hỏi x1 có thỏa mãn điều kiện nói trên không ? Tương tự, đối với x2 ?
Vậy nghiệm của phương trình đã cho là:....
- Điều kiện: x ≠ ±3
- Khử mẫu và biến đổi, ta được: x2 – 3x + 6 = x + 3 ⇔ x2 – 4x + 3 = 0.
- Nghiệm của phương trình x2 – 4x + 3 = 0 là: x1 = 1; x2 = 3
x1 có thỏa mãn điều kiện nói trên
x2 không thỏa mãn điều kiện nói trên
Vậy nghiệm của phương trình đã cho là: x = 1
Đúng 0
Bình luận (0)
Giải phương trình
x
2
−
3
x
+
6
x
2
−
9
1
x
−
3
Bằng cách điền vào các chỗ trống (…) và trả lời các câu hỏi.- Điều kiện: x ≠ …- Khử mẫu và biến đổi, ta được:
x
2...
Đọc tiếp
Giải phương trình
x 2 − 3 x + 6 x 2 − 9 = 1 x − 3
Bằng cách điền vào các chỗ trống (…) và trả lời các câu hỏi.
- Điều kiện: x ≠ …
- Khử mẫu và biến đổi, ta được: x 2 – 3 x + 6 = … ⇔ x 2 – 4 x + 3 = 0 .
- Nghiệm của phương trình x 2 – 4 x + 3 = 0 l à : x 1 = … ; x 2 = …
Hỏi x 1 có thỏa mãn điều kiện nói trên không ? Tương tự, đối với x 2 ?
Vậy nghiệm của phương trình đã cho là:....
- Điều kiện: x ≠ ±3
- Khử mẫu và biến đổi, ta được: x 2 – 3 x + 6 = x + 3 ⇔ x 2 – 4 x + 3 = 0 .
- Nghiệm của phương trình x 2 – 4 x + 3 = 0 l à : x 1 = 1 ; x 2 = 3
x 1 có thỏa mãn điều kiện nói trên
x 2 không thỏa mãn điều kiện nói trên
Vậy nghiệm của phương trình đã cho là: x = 1
Đúng 0
Bình luận (0)
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình (2 - 3 ) x 2 + 4x + 2 + 2 = 0
Ta có: ∆ ’ = 2 2 – (2 - 3 )(2 + 2 ) =4 -4 - 2 2 +2 3 + 6
= 2 3 - 2 2 + 6 >0
Phương trình 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
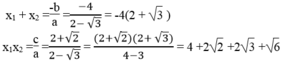
Đúng 0
Bình luận (0)
Cho phương trình ẩn x : x2 - 4x + m -1 =0 (1)
a) Giải phương trình (1) với m = -4
b) Với x1,x2 là nghiệm phương trình (1). Tìm giá trị của m, biết x1-x2= 2
Bài 5: Cho phương trình x2 – 4x + 2m - 3 = 0 a) Tìm điều kiện của m để phương trình có 2 nghiệm x1, X2 phân biệt thoả tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau. b) Tìm m để phương trình có 2 nghiệm X), x2 thoả mãn điều kiện x1 = 3x2
a) Ta có: \(\Delta=\left(-4\right)^2-4\cdot1\cdot\left(2m-3\right)=16-4\left(2m-3\right)\)
\(\Leftrightarrow\Delta=16-8m+12=-8m+28\)
Để phương trình có hai nghiệm x1;x2 phân biệt thì \(-8m+28>0\)
\(\Leftrightarrow-8m>-28\)
hay \(m< \dfrac{7}{2}\)
Với \(m< \dfrac{7}{2}\) thì phương trình có hai nghiệm phân biệt x1;x2
nên Áp dụng hệ thức Viet, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left(-4\right)}{1}=4\\x_1\cdot x_2=\dfrac{2m-3}{1}=2m-3\end{matrix}\right.\)
Để phương trình có hai nghiệm x1,x2 phân biệt thỏa mãn tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau thì
\(\left\{{}\begin{matrix}m< \dfrac{7}{2}\\4+2m-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\2m+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\2m=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\m=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m=-\dfrac{1}{2}\)
Vậy: Khi \(m=-\dfrac{1}{2}\) thì phương trình có hai nghiệm x1,x2 phân biệt thỏa mãn tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau
Đúng 1
Bình luận (0)
Gọi
x
1
,
x
2
là 2 nghiệm của phương trình
4
x
+
1
-
5
.
2
x
+
1
+
4
0
. Khi đó giá trị
S
x
1
+...
Đọc tiếp
Gọi x 1 , x 2 là 2 nghiệm của phương trình 4 x + 1 - 5 . 2 x + 1 + 4 = 0 . Khi đó giá trị S = x 1 + x 2 là
A. -1
B. 0
C. 1
D. 2