d) e)
; g)
.

Những câu hỏi liên quan
a/b = c/d=e/f CMR:
a) a/b=c/d=e/f=a+c+e/b+d+f
b) a/b=c/d=e/f =a-c+e/b-d+f
c) a/b=c/d=e/f =a-c-e/b-d-f
cho 5 số nguyên a,b,c,d,e thỏa mãn:
a+b+c+d+e=0
a+b=c+d=d+e=-2
tìm giá trị:c*d*e
`a+b=c+d=-2` thay vào `a+b+c+d+e=0` ta có:
`e-4=0=>e=4`
Mà `d+e=-2=>d=-6`
Mà `c+d=-2`
`=>c=-2-d=4`
`=>c.d.e=4.4.(-6)=-96`
Đúng 0
Bình luận (0)
\(a+b=c+d=d+e=-2\)
\(a+b+c+d+e=0\)
\(\Leftrightarrow-2+\left(-2\right)+e=0\Leftrightarrow e=4\)
\(d+e=0\Leftrightarrow-2+d=0\Leftrightarrow d=2\)
\(c+d=-2\Leftrightarrow c+2=-2\Leftrightarrow c=-4\)
\(\Rightarrow c.d.e=-4.2.4=-32\)
Đúng 0
Bình luận (0)
Vẽ hai đường thẳng d, e và bốn điểm M, N, P, Q thỏa mãn các điều kiện sau:i) P
∈
e, P
∈
dii) N
∈
d, N
∉
eiii) M
∈
e , M
∉
div) Q
∉
e, Q
∉
d
Đọc tiếp
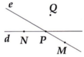
Vẽ hai đường thẳng d, e và bốn điểm M, N, P, Q thỏa mãn các điều kiện sau:
i) P ∈ e, P ∈ d
ii) N ∈ d, N ∉ e
iii) M ∈ e , M ∉ d
iv) Q ∉ e, Q ∉ d
cho 5 số nguyên dương a;b;c;d;e .chứng minh rằng (a-b)(a-c)(a-d)(a-e)(b-c)(b-d)(b-e)(c-d)(c-e)(d-e) chia hết cho 288
Là:
a>b,c,d,e
b>c,d,e
c>d,e
d>e
đúng ko?
Đúng 0
Bình luận (0)
Thử dùng đi-rích-lê+ modun=((
Đặt biểu thức cần chứng minh là P
Ta có:\(288=3^2\cdot2^5\)
Xét 4 số \(a,b,c,d\) thì tồn tại 2 số có cùng số dư khi chia cho 3.
Giả sử \(a\equiv b\left(mod3\right)\Rightarrow a-b⋮3\left(1\right)\)
Xét 4 số \(b,d,c,e\) thì tông tại 2 số có cùng số dư khi chia cho 3.
Giả sử \(c\equiv d\left(mod3\right)\Rightarrow c-d⋮3\left(2\right)\)
Từ (1);(2) suy ra \(P⋮9\left(3\right)\)
Trong 5 số đã cho thì chắc chắn có 3 số cùng tính chẵn lẻ.
Chúng ta cần xét các trường hợp có thể xảy ra.
4 số chẵn giả sử các số đó là:a,b,c,d.
Đặt \(a=2a_1;b=2b_1;c=2c_1;d=2d_1\) với \(a_1;b_1;c_1;d_1\in N\)
\(\Rightarrow P=\left(2a_1-2b_1\right)\left(2a_1-2c_1\right)\left(2a_1-2d_1\right)\left(2a_1-e\right)\left(2b_1-2c_1\right)\left(2b_1-2d_1\right)\left(2b_1-e\right)\left(2c_1-2d_1\right)\left(2c_1-e\right)\left(2d_1-e\right)\)
\(\Rightarrow P=2^5\cdot\left(a_1-b_1\right)\left(a_1-c_1\right)\left(a_1-d_1\right)\left(2a_1-e\right)\left(b_1-c_1\right)\left(b_1-d_1\right)\left(2b_1-e\right)\left(2c_1-2d_1\right)\left(2c_1-e\right)\left(2d_1-e\right)\)
Giả sử 3 số a,b,c chẵn còn d,e lẻ.
Đặt \(a=2a_2;b=2b_2;c=2c_2;d=2d_2+1;e=2e_2+1\)
\(\Rightarrow P=\left(2a_2-2b_2\right)\left(2a_2-2c_2\right)\left(2b_2-2c_2\right)Q\)
\(\Rightarrow P=16\left(a_2-b_2\right)\left(a_2-c_2\right)\left(b_2-c_2\right)\left(d_2-e_2\right)\cdot Q\)
Xét 3 số \(a_2;b_2;c_2\) thì có 2 số chia cho 2 có cùng số dư.
Giả sử 2 số đó là \(a_2;b_2\)
\(\Rightarrow a_2-b_2⋮2\Rightarrow P⋮32\)
Giả sử có 3 số lẻ là \(a,b,c\) và 2 số chẵn là \(d,e\)
Đặt \(a=a_3+1;b=b_3+1;c=c_3+1;d=2d_3;e=2e_3\)
Chứng minh tương tự như TH2 thì P chia hết cho 32.
Trong cả 3 trường hợp đều chia hết cho 32 nên P chia hết cho 32
Mà \(\left(32;9\right)=1\Rightarrow P⋮32\cdot9=288\left(đpcm\right)\)
Đúng 0
Bình luận (0)
cho 5 số nguyên dương a;b;c;d;e .chứng minh rằng (a-b)(a-c)(a-d)(a-e)(b-c)(b-d)(b-e)(c-d)(c-e)(d-e) chia hết cho 288
Đặt P=(a-b)(a-c)(a-d)(a-e)(b-c)(b-d)(b-e)(c-d)(c-e)(d-e)
*Với 5 số a,b,c,d,e có ít nhất 2 số khi chia cho 3 có cùng số dư, không mất tính tổng quát giả sử hai số đó là a và b khi đó a-b chia hết cho 3. Bỏ đi b, xét 4 số còn lại. Trong 4 số này có ít nhất 2 số khi chia cho 3 có cùng số dư, không mất tính tổng quát giả sử 2 số đó là d và e khi đó d-e chia hết cho 3. =>P chia hết cho 9(1).
*Trong 5 số tự nhiên có ít nhất 3 số cùng tính chẵn lẻ.
-Nếu có cả 5 số cùng tính chẵn lẻ hiển nhiên tất cả các thừa số của P đều chia hết cho 2.
=>P chia hết cho
=>P chia hết cho
=>P chia hết cho 32
-Nếu trong 5 số có 4 số cùng tính chẵn lẻ, 4 số này tạo ra 6 thừa số của tích, mà mỗi tích đều chia hết cho 2.
=>P chia hết cho
=>P chia hết cho
=>P chia hết cho 32
-Nếu trong 5 số có 3 số cùng tính chẵn, không mất tính tổng quát giả sử đó là a,b,c.
Đặt a=2.m,b=2.n,c=2.p,d=2.q+1,e=2.l+1
=>P là tích của 16(m-n)(m-p)(n-p)(q-l) và 6 thừa số lẻ. Trong 3 số m,n,p có ít nhất 2 số cùng tính chẵn lẻ, chúng tạo ra 1 thừa số chia hết cho 2.
=>P chia hết cho 32
Tương tự với 3 số cùng lẻ và 2 số cùng chẵn thì P chia hết cho 32.
=> P chia hết cho 32(2).
Từ (1) và (2) ta thấy: P chia hết cho 9 và 32.
Mà (9,32)=1
=>P chia hết cho 9.32.
=>P chia hết cho 288
=> ĐPCM
Đúng 1
Bình luận (0)
Đặt P=(a-b)(a-c)(a-d)(a-e)(b-c)(b-d)(b-e)(c-d)(c-e)(d-e)
*Với 5 số a,b,c,d,e có ít nhất 2 số khi chia cho 3 có cùng số dư, không mất tính tổng quát giả sử hai số đó là a và b khi đó a-b chia hết cho 3. Bỏ đi b, xét 4 số còn lại. Trong 4 số này có ít nhất 2 số khi chia cho 3 có cùng số dư, không mất tính tổng quát giả sử 2 số đó là d và e khi đó d-e chia hết cho 3. =>P chia hết cho 9(1).
*Trong 5 số tự nhiên có ít nhất 3 số cùng tính chẵn lẻ.
-Nếu có cả 5 số cùng tính chẵn lẻ hiển nhiên tất cả các thừa số của P đều chia hết cho 2.
=>P chia hết cho
=>P chia hết cho
=>P chia hết cho 32
-Nếu trong 5 số có 4 số cùng tính chẵn lẻ, 4 số này tạo ra 6 thừa số của tích, mà mỗi tích đều chia hết cho 2.
=>P chia hết cho
=>P chia hết cho
=>P chia hết cho 32
-Nếu trong 5 số có 3 số cùng tính chẵn, không mất tính tổng quát giả sử đó là a,b,c.
Đặt a=2.m,b=2.n,c=2.p,d=2.q+1,e=2.l+1
=>P là tích của 16(m-n)(m-p)(n-p)(q-l) và 6 thừa số lẻ. Trong 3 số m,n,p có ít nhất 2 số cùng tính chẵn lẻ, chúng tạo ra 1 thừa số chia hết cho 2.
=>P chia hết cho 32
Tương tự với 3 số cùng lẻ và 2 số cùng chẵn thì P chia hết cho 32.
=> P chia hết cho 32(2).
Từ (1) và (2) ta thấy: P chia hết cho 9 và 32.
Mà (9,32)=1
=>P chia hết cho 9.32.
=>P chia hết cho 288
=> ĐPCM
Đúng 0
Bình luận (0)
Đặt P=(a-b)(a-c)(a-d)(a-e)(b-c)(b-d)(b-e)(c-d)(c-e)(d-e)
*Với 5 số a,b,c,d,e có ít nhất 2 số khi chia cho 3 có cùng số dư, không mất tính tổng quát giả sử hai số đó là a và b khi đó a-b chia hết cho 3. Bỏ đi b, xét 4 số còn lại. Trong 4 số này có ít nhất 2 số khi chia cho 3 có cùng số dư, không mất tính tổng quát giả sử 2 số đó là d và e khi đó d-e chia hết cho 3. =>P chia hết cho 9(1).
*Trong 5 số tự nhiên có ít nhất 3 số cùng tính chẵn lẻ.
-Nếu có cả 5 số cùng tính chẵn lẻ hiển nhiên tất cả các thừa số của P đều chia hết cho 2.
=>P chia hết cho
=>P chia hết cho
=>P chia hết cho 32
-Nếu trong 5 số có 4 số cùng tính chẵn lẻ, 4 số này tạo ra 6 thừa số của tích, mà mỗi tích đều chia hết cho 2.
=>P chia hết cho
=>P chia hết cho
=>P chia hết cho 32
-Nếu trong 5 số có 3 số cùng tính chẵn, không mất tính tổng quát giả sử đó là a,b,c.
Đặt a=2.m,b=2.n,c=2.p,d=2.q+1,e=2.l+1
=>P là tích của 16(m-n)(m-p)(n-p)(q-l) và 6 thừa số lẻ. Trong 3 số m,n,p có ít nhất 2 số cùng tính chẵn lẻ, chúng tạo ra 1 thừa số chia hết cho 2.
=>P chia hết cho 32
Tương tự với 3 số cùng lẻ và 2 số cùng chẵn thì P chia hết cho 32.
=> P chia hết cho 32(2).
Từ (1) và (2) ta thấy: P chia hết cho 9 và 32.
Mà (9,32)=1
=>P chia hết cho 9.32.
=>P chia hết cho 288
=> ĐPCM
bấm đúng cho tớ nha các bạn
Đúng 0
Bình luận (0)
cho 3 so thuc duong d e f thoa man \(\frac{d}{e+f}+\frac{e}{d+f}+\frac{f}{d+e}=\frac{3}{2}\)
CMR d=e=f
Áp dụng bất đẳng thức Nesbitt với 3 số dương d,e,f ta có: \(\frac{d}{e+f}+\frac{e}{d+f}+\frac{f}{d+e}\ge\frac{3}{2}\)
Dấu "=" xảy ra khi d=e=f
Đúng 0
Bình luận (0)
Chứng minh rằng \(\frac{d}{e+f}+\frac{e}{d+f}+\frac{f}{d+e}\ge\frac{3}{2}\)\(\forall d,e,f>0\)
\(\Rightarrow\frac{d}{e+f}+1+\frac{e}{d+f}+1+\frac{f}{d+e}+1\ge\frac{9}{2}\)
\(\Rightarrow\frac{d+e+f}{e+f}+\frac{d+e+f}{d+f}+\frac{d+e+f}{d+e}\ge\frac{9}{2}\)
\(\Rightarrow\left(d+e+f\right)\left(\frac{1}{e+f}+\frac{1}{d+f}+\frac{1}{d+e}\right)\ge\frac{9}{2}\)
\(\Rightarrow2\left(d+e+f\right)\left(\frac{1}{e+f}+\frac{1}{d+f}+\frac{1}{d+e}\right)\ge9\)
\(\Rightarrow\left(e+f+d+f+d+e\right)\left(\frac{1}{e+f}+\frac{1}{d+f}+\frac{1}{d+e}\right)\ge9\)
Áp dụng bất đẳng thức Cauchy
\(\Rightarrow\left(e+f+d+f+d+e\right)\left(\frac{1}{e+f}+\frac{1}{d+f}+\frac{1}{d+e}\right)\ge9\sqrt[3]{\left(e+f\right)\left(d+f\right)\left(d+e\right).\frac{1}{\left(e+f\right)\left(d+f\right)\left(d+e\right)}}=9\)
Vậy ta có đpcm
Dấu " = " xảy ra khi \(e=d=f\) ( đpcm )
Đúng 0
Bình luận (0)
Cho a,b,c,d,e thỏa mãn a^2+b^2+c^2+d^2+e^2=a(b+c+d+e). CMR b=c=d=e
Lời giải:
$a^2+b^2+c^2+d^2+e^2=a(b+c+d+e)$
$\Leftrightarrow 4a^2+4b^2+4c^2+4d^2+4e^2-4a(b+c+d+e)=0$
$\Leftrightarrow (a^2+4b^2-4ab)+(a^2-4c^2-4ac)+(a^2+4d^2-4ad)+(a^2+4e^2-4ae)=0$
$\Leftrightarrow (a-2b)^2+(a-2c)^2+(a-2d)^2+(a-2e)^2=0$
Ta thấy: $(a-2b)^2,(a-2c)^2,(a-2d)^2,(a-2e)^2\geq 0$ với mọi $a,b,c,d,e$ thực
Do đó để tổng của chúng bằng $0$ thì:
$(a-2b)^2=(a-2c)^2=(a-2d)^2=(a-2e)^2=0$
$\Leftrightarrow 2b=2c=2d=2e=a$
$\Rightarrow b=c=d=e$
Đúng 0
Bình luận (0)
Cho a,b,c,d,e thỏa mãn a^2+b^2+c^2+d^2+e^2=a(b+c+d+e). CMR b=c=d=e
\(\left(\dfrac{a}{2}-b\right)^2\ge0\Leftrightarrow\dfrac{a^2}{4}-ab+b^2\ge0\Leftrightarrow\dfrac{a^2}{4}+b^2\ge ab\)
CMTT ta được: \(\left\{{}\begin{matrix}\dfrac{a^2}{4}+c^2\ge ac\\\dfrac{a^2}{4}+d^2\ge ad\\\dfrac{a^2}{4}+e^2\ge ae\end{matrix}\right.\)
\(\Rightarrow4.\dfrac{a^2}{4}+b^2+c^2+d^2+e^2\ge ab+ac+ad+ae\)
\(\Rightarrow a^2+b^2+c^2+d^2+e^2\ge a\left(b+c+d+e\right)\)
\(ĐTXR\Leftrightarrow\dfrac{a}{2}=b=c=d=e\)
Đúng 0
Bình luận (0)
Cho a,b,c,d,e thuộc N thõa mãn \(a^b=b^e=c^d=d^e=e^a\)
CMR: a=b=c=d=e
Không mất tính tổng quát, giả sử \(a\ge b\)
Vì \(a^b=b^c\Rightarrow b\le c\)
Vì \(b^c=c^d\Rightarrow c\ge d\)
Vì \(c^d=d^e\Rightarrow d\le e\)
Vì \(d^e=e^a\Rightarrow e\ge a\)
Vì \(e^a=a^b\Rightarrow a\le b\)
Suy ra \(a=b\Rightarrow a=b=c=d=e\)
Đpcm
Đúng 0
Bình luận (0)
+Nếu một trong năm số a,b,c,d,e=1
=>a=b=c=d=e=1
+Không mất tính tổng quát giả sử a>1.Từ ab=bc=>b>1
Tương tự như vậy c,d,e>1. Như vậy tất cả các hàm mũ mà a,b,c,d,e là cơ số thì đều là hàm tăng.
Không mất tính tổng quát giả sử \(a\le b\)
Từ \(a^b=b^c\Rightarrow\frac{a^b}{b^b}=\frac{b^c}{b^b}\Rightarrow\left(\frac{a}{b}\right)^b=b^{c-b}\)
Do \(\frac{a}{b}\le1\Rightarrow b^{c-b}\le1=b^0\Rightarrow c-b\le0\Rightarrow c\le b\)
Tương tự như vậy với các đẳng thức còn lại
\(\begin{cases}c\le b\\b^c=c^d\end{cases}\)\(\Rightarrow\begin{cases}\frac{b}{c}\ge1\\\left(\frac{b}{c}\right)^c=c^{d-c}\end{cases}\Rightarrow c\le d\)
\(\begin{cases}c\le d\\c^d=d^e\end{cases}\Rightarrow...\Rightarrow e\le d\)
\(\begin{cases}e\le d\\d^e=e^a\end{cases}\Rightarrow...\Rightarrow e\le a\)
\(\begin{cases}e\le a\\e^a=a^b\end{cases}\Rightarrow....\Rightarrow b\le a\)
Kết hợp \(a\le b\) và \(b\le a\) ta có a=b.Tiếp tục như vậy b=c, c=d, d=e
Vậy phải có a=b=c=d=e
Đúng 0
Bình luận (0)
Cho a, b, c, d, e, g >0 thoả mãn a/b= b/c= c/d= d/e= e/g. Chứng minh rằng:
(a+ b+ c+ d+ e/ b+ c+ d+ e+ g)^2020= a^404/ g^404
Áp dụng dãy tỉ số bằng nhau:
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{d}{e}=\frac{e}{g}=\frac{a+b+c+d+e}{b+c+d+e+g}\)
=> \(\left(\frac{a}{b}\right)^{404}.\left(\frac{b}{c}\right)^{404}.\left(\frac{c}{d}\right)^{404}.\left(\frac{d}{e}\right)^{404}.\left(\frac{e}{g}\right)^{404}\)
\(=\left(\frac{a+b+c+d+e}{b+c+d+e+g}\right)^{404}.\left(\frac{a+b+c+d+e}{b+c+d+e+g}\right)^{404}.\left(\frac{a+b+c+d+e}{b+c+d+e+g}\right)^{404}.\left(\frac{a+b+c+d+e}{b+c+d+e+g}\right)^{404}.\left(\frac{a+b+c+d+e}{b+c+d+e+g}\right)^{404}\)
=> \(\left(\frac{abcde}{bcdeg}\right)^{404}=\left(\frac{a+b+c+d+e}{b+c+d+e+g}\right)^{404+404+404+404}\)
=> \(\frac{a^{404}}{g^{404}}=\left(\frac{a+b+c+d+e}{b+c+d+e+g}\right)^{2020}\)