Cho tam giác vuông ABC có A=90°. D là một điểm nằm giữa A và B . E là một điểm nằm giữa A và C. nối B với E , D với E .chứng minh :
a, BE < BC.
b, DE < BC
Những câu hỏi liên quan
Cho tam giác vuông ABC có A=90°. D là một điểm nằm giữa A và B . E là một điểm nằm giữa A và C. nối B với E , D với E .chứng minh :
a, BE < BC.
b, DE < BC
Cho tam giác vuông ABC có A=90°. D là một điểm nằm giữa A và B . E là một điểm nằm giữa A và C. nối B với E , D với E .chứng minh :
a, BE < BC.
b, DE < BC
Giải:
a) Ta có: \(AE< AC\)
\(\Rightarrow BE< BC\) ( hình chiếu bé hơn thì đường xiên cũng bé hơn )
b) Ta có: \(AD< AB\Rightarrow DE< BE\)
Mà BE < BC nên DE < BC ( đpcm )
Vậy...
Đúng 0
Bình luận (0)
1) Cho góc xAy = 90 độ. Trên cạnh Ax lấy hai điểm B và D ( D nằm giữa A và B ) , trên cạnh Ay lấy hai điểm C và E ( C nằm giữa A và E ) sao cho AD = AC ; AB = AE
a) Chứng minh : tam giác ABC = tam giác AED ; tam giác BCE = tam giác EDB
b) Đường thẳng qua A vuông góc với BC tại H và cắt DE tại M. Chứng minh M là trung điểm của DE
Cho tam giác ABC có ˆBAC���^ là một góc tù. Lấy điểm D nằm giữa A và B; lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE BC.
Đọc tiếp
Cho tam giác ABC có là một góc tù. Lấy điểm D nằm giữa A và B; lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE < BC.
góc CAD>90 độ
=>góc CED>90 độ
=>ED<CD
goc CDB=góc DAC+góc ACD
=>góc CDB>90 độ
=>CD<BC
=>ED<BC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân , AB = AC . Trên cạnh AC lấy điểm D và trên tia AB lấy E ( B nằm giữa A và E ) sao cho BE=CD. Nối D với E cắt BC ở M. Chứng Minh : M là trung điểm của DE
Cho tam giác ABC có \(\widehat {BAC}\) là góc tù. Lấy điểm D nằm giữa A và B, lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE < BC.
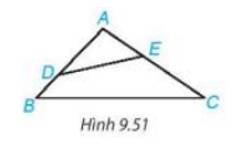
Ta có \(\widehat {BAC}\) là góc tù nên \(\widehat {ADE},\widehat {AED}\) là các góc nhọn
\( \Rightarrow \widehat {DEC}\) là góc tù
\( \Rightarrow DE < DC\) (quan hệ giữa góc và cạnh đối diện trong tam giác DEC). (1)
Xét tam giác ADC có:
\(\widehat {DAC}\) là góc tù nên \(\widehat {ADC},\widehat {ACD}\) là các góc nhọn
\( \Rightarrow \widehat {BDC}\) là góc tù.
\( \Rightarrow DC < BC\) (quan hệ giữa góc và cạnh đối diện trong tam giác BDC) (2)
Từ (1) và (2) suy ra: BC > DE
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Gọi D là điểm thuộc AC; E là điểm thuộc đường thẳng AB, với B nằm giữa A và E, sao cho CD = BE. Gọi M là giao điểm của DE và BC. Chứng minh rằng : M là trung điểm của DE.
Cho tam giác ABC cân tại A. Gọi D là điểm thuộc AC; E là điểm thuộc đường thẳng AB, với B nằm giữa A và E, sao cho CD = BE. Gọi M là giao điểm của DE và BC. Chứng minh rằng : M là trung điểm của DE.
Cho tam giác ABC có góc A tù, điểm D nằm giữa A và B, điểm E nằm giữa A và C. Chứng minh BC > DE
Bạn tham khảo ở đây nhé!!
https://h.vn/hoi-dap/question/269901.html
hok tốt!!
~
Vì góc bac là góc tú nên độ dài ab lớn
Mà d nằm giữa ba và e năm giữa ac nên
De<bc