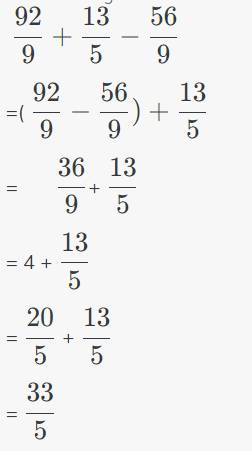#)Giải :

\(8^x-2^x=16^{2011}\)

\(\Leftrightarrow\left(2^3\right)^x-2^x=\left(2^4\right)^{2011}\)

\(\Leftrightarrow2^{3x}-2^x=2^{8044}\)

\(\Leftrightarrow2^{2x}=8044\)

\(\Leftrightarrow2x=8044\)

\(\Leftrightarrow x=4022\)

8^x : 2^x = 16²⁰¹¹

=> 4^x = (4²)²⁰¹¹

=> 4^x = 4^2.2011

=> 4^x = 4⁴⁰²²

=> x = 4022

\(8^x:2^x=16^{2011}\)

\(\left(2^3\right)^x:2^x=\left(2^4\right)^{2011}\)

\(2^{3x}:2^x=2^{8044}\)

\(2^{2x}=2^{8044}\)

\(\Rightarrow2x=8044\)

       \(x=8044:2\)

      \(x=4022\)

        Vậy \(x=4022\)

\(\left(x-2011\right)\left(\frac{1}{12}+\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+\frac{1}{56}+\frac{1}{72}\right)=\frac{16}{9}\)

\(\left(x-2011\right)\cdot\frac{2}{9}=\frac{16}{9}\)

\(x-2011=8\)

\(x=2019\)

\(\frac{x-2011}{12}+\frac{x-2011}{20}+\frac{x-2011}{30}+\frac{x-2011}{42}+\frac{x-2011}{56}+\frac{x-2011}{72}=\frac{16}{9}\)

\(\left(x-2011\right)\left(\frac{1}{12}+\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+\frac{1}{56}+\frac{1}{72}\right)=\frac{16}{9}\)

\(\left(x-2011\right)\left(\frac{1}{3.4}+\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+\frac{1}{7.8}+\frac{1}{8.9}\right)=\frac{16}{9}\)

\(\left(x-2011\right)\left(\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+...+\frac{1}{8}-\frac{1}{9}\right)=\frac{16}{9}\)

\(\left(x-2011\right)\left(\frac{1}{3}-\frac{1}{9}\right)=\frac{16}{9}\)

\(\left(x-2011\right)\frac{2}{9}=\frac{16}{9}\)

\(x-2011=8\Rightarrow x=2019\)

\(\left(2^3\right)^n\)\(:2^n\)\(=\left(2^4\right)^{2021}\)

\(2^{3n}\)\(:2^n\)\(=2^{4x2021}\)\(=2^{8084}\)

\(2^{3n-n}\)\(=2^{8084}\)

\(=>3n-n=8084\)

\(2n=8084\)

\(n=8084:2=4042\)

\(=>n=4042\)

A=\(\left|x^2+y^2+5+2x-4y\right|-\left|-\left(x+y-1\right)^2+2xy\right|\)

\(\Leftrightarrow A=x^2+y^2+5+2x-4y-\left|-\left(x^2+2xy-2x-2y+y^2+1\right)\right|+2xy\)

\(\Leftrightarrow A=x^2+y^2+5+2x-4y+x^2-2xy+2x+2y-y^2-1+2xy\)

\(\Leftrightarrow A=2x^2-4+4x-2y\)

thay \(x=2^{2011};y=16^{503}\) vào A ta được:

\(2.\left(2^{2011}\right)^2-4+4.\left(2^{2011}\right)-2.\left(16^{503}\right)\)

A không có giá trị

 58/7 - (31/9 + 30/7)                  
= 58/7 - 31/9 - 30/7
= (58/7 - 30/7) - 31/9
= 28/7- 31/9
= 4 - 31/9 = 36/9 - 31/9
= 5/9

478/19÷(-5/4)-668/19÷(-5/4)
=(478/19-668/19):(-5/4)
=-10 . (-4/5)
=8

a. 1⋅2⋅3+2⋅4⋅6+3⋅6⋅9+4⋅8⋅12

= 6+2⋅4⋅6+3⋅6⋅9+4⋅8⋅12

= 6+48+3⋅6⋅9+4⋅8⋅12

= 6+48+162+4⋅8⋅12

= 6+48+162+384

= 600

b . Ta có \(A=\frac{2010+2011}{2011+2012}=\frac{2010}{2011+2012}+\frac{2011}{2011+2012}.\)

Ta có : \(\frac{2010}{2011+2012}< \frac{2010}{2011}\) và \(\frac{2011}{2011+2012}< \frac{2011}{2012}\)

=> \(\frac{2010+2011}{2011+2012}< \frac{2010}{2011}+\frac{2011}{2012}\)

=> A < B

a) ĐKXĐ: \(x\notin\left\{0;2\right\}\)

Ta có: \(\dfrac{x+2}{x-2}-\dfrac{1}{x}=\dfrac{2}{x\left(x-2\right)}\)

\(\Leftrightarrow\dfrac{x\left(x+2\right)}{x\left(x-2\right)}-\dfrac{x-2}{x\left(x-2\right)}=\dfrac{2}{x\left(x-2\right)}\)

Suy ra: \(x^2+2x-x+2-2=0\)

\(\Leftrightarrow x^2+x=0\)

\(\Leftrightarrow x\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)

Vậy: S={-1}