ΔABC cân tại A suy ra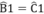 

Ta lại có :

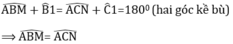
- ΔABM và ΔACN có

      AB = AC (Do ΔABC cân tại A).

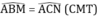
      BM = CN(gt)

⇒ ΔABM = ΔACN (c.g.c)

⇒ AM = AN (hai cạnh tương ứng) ⇒ ΔAMN cân tại A.

Từ đỉnh A kẻ đường cao AH (H thuộc BC) (1)

Ta có : tam giác ABC cân tại A (gt) (2)

Từ(1) và(2)=> HB=HC(=1/2 BC) (3)

Lại có: BM=CN (gt) (4)

M nằm trên tia đối của tia BC, N nằm trên tia đối của tia CB => M,B,C.N thẳng hàng (5)

Từ (3)và (4)=>HB+BM=HC+CN (6)

Từ  (5) và (6)=>AH vừa là đường cao, vừa là đường trung tuyến trong tam giác AMN

=> Tam giác AMN cân tại A (đpcm)

Xét ΔBAM và ΔCAN có 

AB=AC

\(\widehat{ABM}=\widehat{ACN}\)

BM=CN

DO dó: ΔBAM=ΔCAN

Suy ra: AM=AN

hay ΔAMN cân tại A

Mn giúp mik với;-;

a) Ta có: \(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)

\(\widehat{ACN}+\widehat{ACB}=180^0\)(hai góc kề bù)

mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)

nên \(\widehat{ABM}=\widehat{ACN}\)

Xét ΔABM và ΔACN có 

AB=AC(ΔABC cân tại A)

\(\widehat{ABM}=\widehat{ACN}\)(cmt)

BM=CN(gt)

Do đó: ΔABM=ΔACN(c-g-c)

Suy ra: AM=AN(hai cạnh tương ứng)

Xét ΔAMN có AM=AN(cmt)

nên ΔAMN cân tại A(Định nghĩa tam giác cân)

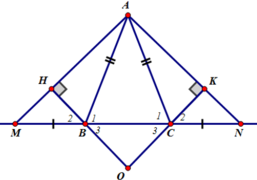
b) Xét ΔHBM vuông tại H và ΔKCN vuông tại K có

BM=CN(gt)

\(\widehat{HMB}=\widehat{KNC}\)(hai góc ở đáy trong ΔAMN cân tại A)

Do đó: ΔHBM=ΔKCN(cạnh huyền-góc nhọn)

Suy ra: BH=CK(hai cạnh tương ứng)

c) Ta có: ΔHBM=ΔKCN(cmt)

nên HM=KN(hai cạnh tương ứng)

Ta có: AH+HM=AM(H nằm giữa A và M)

AK+KN=AN(K nằm giữa A và N)

mà AM=AN(cmt)

và HM=KN(cmt)

nên AH=AK(đpcm)

d) Ta có: ΔHBM=ΔKCN(cmt)

nên \(\widehat{HBM}=\widehat{KCN}\)(hai góc tương ứng)

mà \(\widehat{OBC}=\widehat{HBM}\)(hai góc đối đỉnh)

và \(\widehat{OCB}=\widehat{KCN}\)(hai góc đối đỉnh)

nên \(\widehat{OBC}=\widehat{OCB}\)

Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)

nên ΔOBC cân tại O(Định lí đảo của tam giác cân)

(Bạn tự vẽ hình)

Có tam giác ABC cân tại A 

=> AB = AC và góc ABC = góc ACB

=> góc ABM = góc ACN (vì cùng kề bù với 2 góc bằng nhau)

Xét tam giác ABM và tam giác ACN có:

   AB = AC (cmt)

   góc ABM = goác ACN (cmt)

   BM = CN (gt)

=> tam giác ABM = tam giác ACN (c.g.c)

=> AM = AN (2 cạnh tương ứng)

=> tam giác AMN cân tại A (Đpcm)

Theo câu b ta có ΔBHM = ΔCKN ⇒ HM = KN (hai cạnh tương ứng)

Mà AM = AN ⇒ AM –MH = AK – KN hay AH = AK.