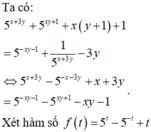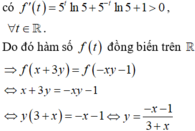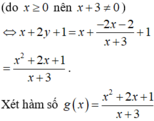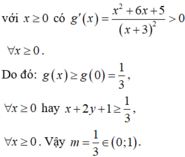Cho là các số dương.Giá trị nhỏ nhất của biểu thức
là
Những câu hỏi liên quan
Câu 10:Cho là các số dương.Giá trị nhỏ nhất của biểu thức \(\frac{a}{b}\)+\(\frac{c}{b}\)+\(\frac{b}{c}\)+\(\frac{a}{c}\)+\(\frac{b}{a}\)+\(\frac{c}{a}\)
Cho là các số dương thỏa mãn Tìm giá trị nhỏ nhất của biểu thức:
Đọc tiếp
Cho 
Tìm giá trị nhỏ nhất của biểu thức:
biến đổi: \(P=1.\left(\dfrac{1}{16x}+\dfrac{1}{4y}+\dfrac{1}{z}\right)=\left(x+y+z\right)\left(\dfrac{1}{16x}+\dfrac{1}{4y}+\dfrac{1}{z}\right)\)
\(P=\left(\dfrac{y}{16x}+\dfrac{x}{4y}\right)+\left(\dfrac{z}{16x}+\dfrac{x}{z}\right)+\left(\dfrac{z}{4y}+\dfrac{y}{z}\right)+\dfrac{21}{16}\)
Áp dụng bất đẳng thức cosi cho từng ngoặc ta được:
\(\dfrac{y}{16x}+\dfrac{x}{4y}\ge2\sqrt{\dfrac{y}{16x}.\dfrac{x}{4y}}=\dfrac{1}{4}\)
hoàn toàn tương tự: \(\dfrac{z}{16x}+\dfrac{x}{z}\ge\dfrac{1}{2}\)
\(\dfrac{z}{4y}+\dfrac{y}{z}\ge1\)
=> P>=49/16
Đúng 0
Bình luận (0)
Cho biểu thức A = 2015 – (a + b), với a > b, a và b là các số có một chữ số. Tìm giá trị nhỏ nhất của A. Giá trị nhỏ nhất của A là ......
2015-(9+8)=1998 vì để giá trị bt nhỏ nhất thì a phải là số tự nhiên lớn nhất là 9. a>b ( a là 9 nên b là 8)
Cho biểu thức:A=\(\dfrac{2x-1}{x+2}\)
a) Tìm số nguyên x để biểu thức A là phân số
b)Tìm các số nguyên x để biểu thức A có giá trị là 1 số nguyên
c)Tìm các số nguyên x để biểu thức A đạt giá trị lớn nhất,giá trị nhỏ nhất
A = \(\dfrac{2x-1}{x+2}\)
a, A là phân số ⇔ \(x\) + 2 # 0 ⇒ \(x\) # -2
b, Để A là một số nguyên thì 2\(x-1\) ⋮ \(x\) + 2
⇒ 2\(x\) + 4 - 5 ⋮ \(x\) + 2
⇒ 2(\(x\) + 2) - 5 ⋮ \(x\) + 2
⇒ 5 ⋮ \(x\) + 2
⇒ \(x\) + 2 \(\in\) { -5; -1; 1; 5}
⇒ \(x\) \(\in\) { -7; -3; -1; 3}
c, A = \(\dfrac{2x-1}{x+2}\)
A = 2 - \(\dfrac{5}{x+2}\)
Với \(x\) \(\in\) Z và \(x\) < -3 ta có
\(x\) + 2 < - 3 + 2 = -1
⇒ \(\dfrac{5}{x+2}\) > \(\dfrac{5}{-1}\) = -5 ⇒ - \(\dfrac{5}{x+2}\)< 5
⇒ 2 - \(\dfrac{5}{x+2}\) < 2 + 5 = 7 ⇒ A < 7 (1)
Với \(x\) > -3; \(x\) # - 2; \(x\in\) Z ⇒ \(x\) ≥ -1 ⇒ \(x\) + 2 ≥ -1 + 2 = 1
\(\dfrac{5}{x+2}\) > 0 ⇒ - \(\dfrac{5}{x+2}\) < 0 ⇒ 2 - \(\dfrac{5}{x+2}\) < 2 (2)
Với \(x=-3\) ⇒ A = 2 - \(\dfrac{5}{-3+2}\) = 7 (3)
Kết hợp (1); (2) và(3) ta có A(max) = 7 ⇔ \(x\) = -3
Đúng 1
Bình luận (0)
Cho x, y là các số thực dương thỏa mãn điều kiện Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức A. 12 B. 8 C. 0 D. 4
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn điều kiện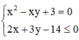 
Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 
A. 12
B. 8
C. 0
D. 4
Đáp án C
Phương pháp:
Rút y theo x từ phương trình (1), thế vào phương trình (2) để tìm khoảng giá trị của x.
Đưa biểu thức P về 1 ẩn x và tìm GTLN, GTNN của biểu thức P.
Cách giải: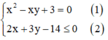 
Ta nhận thấy x = 0 không thỏa mãn phương trình (1), do đó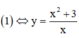 
thế vào (2):
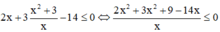
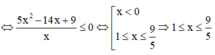
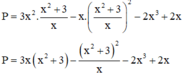
Sử dụng MTCT ta tính được
Đúng 0
Bình luận (0)
Cho các số thực dương x,y thoả: 3 ) 2x + 2 giá trị nhỏ nhất của biểu thức P là ?
Đọc tiếp
Cho các số thực dương x,y thoả: 3
) = 2x + 2
giá trị nhỏ nhất của biểu thức P = 
là ?
Cho ab, là các số thực dương thỏa mãn
1
2
log
2
a
log
2
2
b
. Hỏi giá trị nhỏ nhất của biểu thức sau
P
4
a
3
+
b
3
-
4
log
2
4
a...
Đọc tiếp
Cho ab, là các số thực dương thỏa mãn 1 2 log 2 a = log 2 2 b . Hỏi giá trị nhỏ nhất của biểu thức sau P = 4 a 3 + b 3 - 4 log 2 4 a 3 + b 3 là:
A. -4
B. 4 log 2 6
C. 4 ln 2 - 4 log 2 4 ln 2
D. 4 1 - log 2 3
Đáp án D
Ta có
Đặt
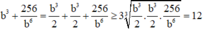
Khi đó
có
Suy ra f(t) là hàm số đồng biến trên
Vậy giá trị nhỏ nhất của P là
Đúng 0
Bình luận (0)
Cho a, b, c là các số dương thỏa điều kiện : a + b + c = 1 . Tìm giá trị nhỏ nhất của biểu thức:
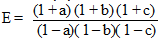
Cho x, y là các số thực lớn hơn 1 sao cho
y
x
.
e
x
e
y
≥
x
y
e
y
e
x
.
Tìm giá trị nhỏ nhất của biểu thức
P
log
x...
Đọc tiếp
Cho x, y là các số thực lớn hơn 1 sao cho y x . e x e y ≥ x y e y e x . Tìm giá trị nhỏ nhất của biểu thức P = log x x y + log y x
A. 2 2
B. 2 2
C. 1 + 2 2 2
D. 1 + 2 2
Cho các số thực x, y với
x
≥
0
thỏa mãn . Gọi m là giá trị nhỏ nhất của biểu thức . Mệnh đề nào sau đây là đúng? A. B. C. D.
Đọc tiếp
Cho các số thực x, y với
x
≥
0
thỏa mãn 
. Gọi m là giá trị nhỏ nhất của biểu thức 
. Mệnh đề nào sau đây là đúng?
A. 
B. 
C. 
D. 
