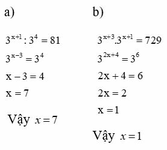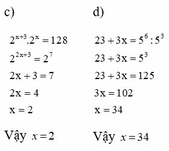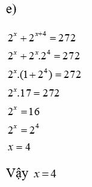a,  3 x + 1 : 3 4 = 81

3 x - 3 = 3 4

x – 3 = 4

x = 7

Vậy x = 7

b,  3 x + 3 . 3 x + 1 = 729

3 2 x + 4 = 3 6

2x + 4 = 6

x = 1

Vậy x = 1

c,  2 x + 3 . 2 x = 128

2 2 x + 3 = 2 7

2x + 3 = 7

x = 2

Vậy x = 2

d,  23 + 3 x = 5 6 : 5 3

23 + 3 x = 5 3

23 + 3x = 125

3x = 102

x = 34

Vậy x = 34

e,  2 x + 2 x + 4 = 272

2 x + 2 x . 2 4 = 272

2 x ( 1 + 2 4 ) = 272

2 x . 17 = 272

2 x = 16

2 x = 2 4

x = 4

Vậy x = 4

2^x + 2^{x + 4} = 272

=> 2^x + 2^x . 2⁴ = 272

=> 2^x .( 1 + 2⁴ ) = 272

=> 2^x . 17 = 272

=> 2^x = 272 : 17 = 16

=> 2^x = 2⁴

=> x = 4

Vậy x = 4

tách số thứ 2 thành 2 ^ x . 2^ 4 có chung nhe làm bình thường nha

\(2^x+2^{x+4}=272\)

\(2^x+2^x\cdot2^4=272\)

\(2^x\left(1+16\right)=272\)

\(2^x\cdot17=272\)

\(2^x=272:17\)

\(2^x=16\)

\(\Rightarrow x=4\)

\(\left(35+x\right)-12=27\\ 35+x=27+12=39\\ x=39-35=4\\ ---\\ 2x-5=3^3:3^2=3\\ 2x=3+5=8\\ x=\dfrac{8}{2}=4\)

1) (35 + x) -12 =27

=>35 + x = 39 => x = 4

2) 2x -5 = 3³ : 3²

=> 2x -5 =3¹ => 2x = 8

=> x = 4

\(\left(x+3\right)\left(2x-4\right)< 0\)

\(\Rightarrow2\left(x+3\right)\left(x-2\right)< 0\)

\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x+3>0\\x-2< 0\end{matrix}\right.\\\left[{}\begin{matrix}x+3< 0\\x-2>0\end{matrix}\right.\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x>-3\\x< 2\end{matrix}\right.\\\left[{}\begin{matrix}x< -3\\x>2\end{matrix}\right.\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x>-3\\x< 2\end{matrix}\right.\)

\(\Rightarrow-3< x< 2\)

giai ro ra ho mik di...

\(\left(x+3\right)\left(2x-4\right)< 0\)

TH1: \(\left\{{}\begin{matrix}x+3>0\\2x-4< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>-3\\x< 2\end{matrix}\right.\) \(\Leftrightarrow-3< x< 2\)

TH2: \(\left\{{}\begin{matrix}x+3< 0\\2x-4>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x< -3\\x>2\end{matrix}\right.\)\(\Leftrightarrow x\in\varnothing\)

Vậy \(-3< x< 2\)

Có: (x + 3)(2x - 4) < 0 \(\Leftrightarrow\) x + 3 và 2x - 4 trái dấu

+) Xét: x + 3 < 0 => x < -3

2x - 4 > 0=>  x > 2 

=> 2 < x < -3 (vô lí) => loại

+) Xét: x + 3 > 0 => x > -3  

2x - 4 < 0 => x < 2

=> -3 < x < 2 (tm)

Vậy... 

\(\left|2x-1\right|-x=4\Leftrightarrow\left|2x-1\right|=4+x\)          (1)

+)TH1: \(2x-1\ge0\Leftrightarrow x\ge\frac{1}{2}\)   thì ph(1) trở thành

    \(2x-1=4+x\Leftrightarrow x=5\) (tm)

+)TH2: \(2x-1< 0\Leftrightarrow x< \frac{1}{2}\) thì pt(1) trở thành

  \(1-2x=4+x\Leftrightarrow-3x=3\Leftrightarrow x=-1\) (tm)

Vậy x={-1;5}

Vẫn thức à

(2x+4).(x+4)<0

=> Phải có 1 thừa số lớn hơn 0 và 1 thừa số nhỏ hơn 0

TH1

2x+4>0 và x+4<0

2x+4>0 => 2x>-4  =>x>-2 (1)

x+4<0 =>x<-4 (2)

(1) và (2) ko thể cùng xảy ra, vậy TH1 loại

TH2 2x+4<0 và x+4>0

2x+4<0 =>x<-2 (3)

x+4>0 =>x>-4  (4)

Từ (3) và (4) => -2<x<-4

Vậy x=-3

\(\left(2x+4\right)\left(x+4\right)< 0\)

\(\Rightarrow2\left(x+2\right)\left(x+4\right)< 0\)

\(\Rightarrow\left(x+2\right)\left(x+4\right)< 0\)

\(\Rightarrow\hept{\begin{cases}x+2< 0\\x+4>0\end{cases}}\) hoặc \(\hept{\begin{cases}x+2>0\\x+4< 0\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}x< -2\\x>-4\end{cases}}\) hoặc \(\hept{\begin{cases}x>-2\\x< -4\end{cases}}\left(loại\right)\)

\(\Rightarrow-4< x< -2\)

Mà \(x\in Z\)

\(\Rightarrow x=-3\)

x=-3 nha bạn 

chúc bạn học giỏi nha bạn