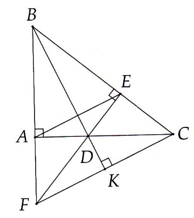
Cho tam giác ABC vuông tại A có góc B=35°
A). Trên cạnh BC lấy điểm D sao cho BD=BA.Tia phân giác của góc B cắt AC ở điểm E. CM:tam giác BEA= tam giác BED
B). Qua C kẻ 1 đường thẳng vuông góc với BE tại H. CH cắt đường thẳng AB tại F. CMR: tam giác BHF=tam giác BHC
C. CM: tam giác BAC= tam giác BDF và D,E,F thẳng hàng
Cho hình vẽ và cách giải chi tiết nha m.n