cho dãy số (sn) với snsin(4n−1)frac{pi}{6} .
chứng minh rằng snsn+3 với mọi n≥1
Đọc tiếp
cho dãy số (sn) với sn=sin(4n−1)\(\frac{\pi}{6}\) .
chứng minh rằng sn=sn+3 với mọi n≥1
Những câu hỏi liên quan
Chứng minh rằng với n thộc N, ta có: 1/1.6 + 1/6.11 + 1/11.16 + ... + 1/(Sn+1).(Sn+6) = n+1/Sn+6
Chứng minh rằng với mọi SN n thì \(\frac{2n+1}{2n.\left(n+1\right)}\) là phân số tối giản
Cho dãy u(n) thỏa mãn
log
3
u
1
2
-
3
log
u
5
log
3
u
2
+
9
-
log
u
1
6
và
u
n...
Đọc tiếp
Cho dãy u(n) thỏa mãn log 3 u 1 2 - 3 log u 5 = log 3 u 2 + 9 - log u 1 6 và u n + 1 = u n + 3 u 1 > 0 với mọi n≥1 Đặt S n = u 1 + u 2 + . . . + u n Tìm giá trị nhỏ nhất của n để S n > 5 n 2 + 2018 2
A. 1647
B. 1650
C. 1648
D. 1165
Với mỗi số nguyên dương n, đặt s_{n} (2 - sqrt{3})^n + (2 + sqrt{3})^na) Chứng minh rằng: s_{n+2} 4s_{n+1} - s_{n}b) Chứng minh rằng sn là số nguyên với mọi số nguyên dương n và tìm số dư của s2018 khi chia cho 3.c) Chứng minh rằng [(2 + sqrt{3})^n] s_{n} - 1 với mọi số nguyên dương n, trong đó kí hiệu [x] là phần nguyên của số thực x.
Đọc tiếp
Với mỗi số nguyên dương \(n\), đặt \(s_{n} = (2 - \sqrt{3})^n + (2 + \sqrt{3})^n\)
a) Chứng minh rằng: \(s_{n+2} = 4s_{n+1} - s_{n}\)
b) Chứng minh rằng sn là số nguyên với mọi số nguyên dương n và tìm số dư của s2018 khi chia cho 3.
c) Chứng minh rằng \([(2 + \sqrt{3})^n] = s_{n} - 1\) với mọi số nguyên dương \(n\), trong đó kí hiệu [x] là phần nguyên của số thực \(x\).
Gọi Sn là tập hợp của các số tự nhiên mà n chia hết cho nó (Sn={1;2;3;6})
a) Viết S8, S9, S12.
b) Chứng minh nếu M ⋮ n thì Sn C Sm
c) Cho Sn C Sm, chứng rằng M ⋮ n
Trả lời giúp mik nha.
a: S8={1;2;4;8}
S9={1;3;9}
S12={1;2;3;4;6;12}
b: M chia hết cho n
=>\(n\inƯ\left(m\right)\)
=>Ước của n chắc chắn sẽ là ước của m
=>\(S_n\subset S_M\)
c: \(S_n\subset S_m\)
=>Ước của n là ước của m
=>n là ước của m
=>\(m⋮n\)
Đúng 1
Bình luận (0)
Chứng minh các đẳng thức sau với
n
∈
N
∗
S
n
sin
x
+
sin
2
x
+
.
.
.
+
sin
n
x
sin...
Đọc tiếp
Chứng minh các đẳng thức sau với n ∈ N ∗ S n = sin x + sin 2 x + . . . + sin n x = sin n x 2 . sin n + 1 x 2 sin x 2
iểm tra với n = 1
Giả sử đã có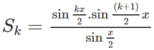 
Viết S k + 1 = S k + sin ( k + 1 ) x sử dụng giả thiết quy nạp và biến đổi ta có
Đúng 0
Bình luận (0)
cho tổng
S
n
1
1
.
2
+
1
2
.
3
+
.
.
.
+
1
n
n
+...
Đọc tiếp
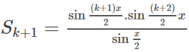
cho tổng S n = 1 1 . 2 + 1 2 . 3 + . . . + 1 n n + 1 với n ∈ N *
a.Tính S1, S2, S3
b.Dự đoán công thức tính tổng Sn và chứng minh bằng quy nạp.
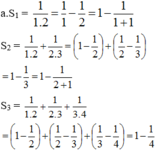
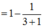
b. Dự đoán: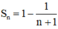 
Ta chứng minh đẳng thức (1) bằng quy nạp
+ Với n = 1 thì (1) đúng.
+ Giả sử (1) đúng với n = k, tức là
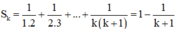
Khi đó:
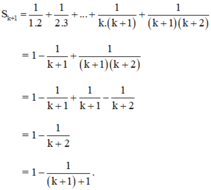
⇒ (1) đúng với n = k + 1, do đó đúng với mọi n ∈ N*
Đúng 0
Bình luận (0)
cho dãy số un xác định bởi u1 = 2021
un+1= (un^2021 - un + 16)/(un^2020 - un + 17)
a) chứng minh un không tồn tại giới hạn hữu hạn
b) đặt Sn = Σ 1/(un^2020 + 3) tính lim Sn
Cho dãy số
u
n
thỏa mãn
u
n
u
n
-
1
với
∀
n
≥
2
và
log
2
u
5
+
log
2
u
9...
Đọc tiếp
Cho dãy số u n thỏa mãn u n = u n - 1 với ∀ n ≥ 2 và log 2 u 5 + log 2 u 9 + 8 = 11 . Đặt tổng sau là S n = u 1 + u 2 + . . . + u n . Tìm số tự nhiên n nhỏ nhất thỏa mãn S n ≥ 20172018 ?
A. 2587.
B. 2590.
C. 2593.
D. 2584.
Cho Sn= \(\frac{1^2-1}{1}+\frac{2^2-1}{2^2}+\frac{3^2-1}{3^2}+...+\frac{n^2-1}{n^2}\)(Với n thuộc N và n>1)
CMR : Sn k là số nguyên