giải giúp câu c ạ !!!!

Những câu hỏi liên quan
Giúp em câu A với câu C giải nhanh giúp em ạ 
a,
c, Gọi \(\left(D_3\right):y=ax+b\) là đt cần tìm
\(\Leftrightarrow\left\{{}\begin{matrix}a=-2;b\ne0\\3x+3=ax+b,\forall x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\-a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-2\end{matrix}\right.\)
Vậy \(\left(D_3\right):y=-2x-2\)
Đúng 0
Bình luận (0)
Giải giúp mik câu b và câu c với ạ
1: Xét ΔABE vuông tại B và ΔADC vuông tại D có
\(\widehat{AEB}=\widehat{ACD}\)
Do đó: ΔABE∼ΔADC
Suy ra: \(\dfrac{AB}{AD}=\dfrac{AE}{AC}\)
hay \(AB\cdot AC=AE\cdot AD\)
Đúng 0
Bình luận (1)
Giải giúp câu câu c thôi ạ. Xin cảm ơn
c) ta có EF là dg tb tg ABC(cmt)
=> EF//BC <=> ED//BC( D thuộc EF) (1)
Ta lại có AECD là hbh ( cmt)
=> AE//CD <=> EB//CD( E thuộc AB) (2)
Từ (1) và (2) => EBCD là hbh( dh1 )
=> EC giao BD tại trung điểm mỗi dg
<=> N td BD; G td EC hay EG=GC
Đúng 1
Bình luận (0)
a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình của ΔBAC
Suy ra: EF//BC và \(EF=\dfrac{BC}{2}\)
hay EF=3,6(cm)
b: Xét tứ giác ADCE có
F là trung điểm của đường chéo AC
F là trung điểm của đường chéo ED
Do đó: ADCE là hình bình hành
Suy ra: AE=CD
mà AE=BD
nên CD=BD
Đúng 1
Bình luận (0)
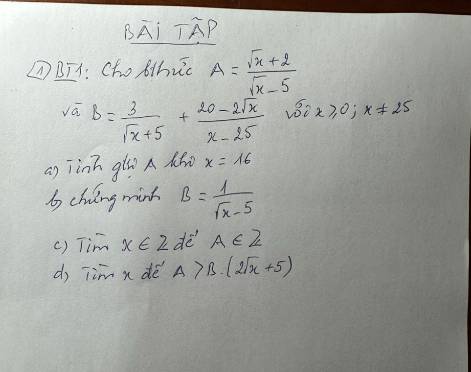
giải giúp mình câu C với câu D với ạ
a) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}\ne5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
Khi \(x=16\Rightarrow A=\dfrac{\sqrt[]{16}+2}{\sqrt[]{16}-5}=\dfrac{4+2}{4-5}=-6\)
b) \(B=\dfrac{3}{\sqrt[]{x}+5}+\dfrac{20-2\sqrt[]{x}}{x-25}\)
B có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x-25\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
\(\Leftrightarrow B=\dfrac{3\left(\sqrt[]{x}-5\right)+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{3\sqrt[]{x}-15+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{\sqrt[]{x}+5}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{1}{\sqrt[]{x}-5}\left(dpcm\right)\)
c) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\in Z\left(x\in Z\right)\)
\(\Leftrightarrow\sqrt[]{x}+2⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\left(\sqrt[]{x}-5\right)⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\sqrt[]{x}+5⋮\sqrt[]{x}-5\)
\(\Leftrightarrow7⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}-5\in U\left(7\right)=\left\{-1;1;-7;7\right\}\)
\(\Leftrightarrow x\in\left\{16;36;144\right\}\)
d) \(A>B\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}>\dfrac{1}{\sqrt[]{x}-5}\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\sqrt[]{x}+2>2\sqrt[]{x}+5\)
\(\Leftrightarrow\sqrt[]{x}< -3\)
mà \(\sqrt[]{x}\ge0\)
\(\Leftrightarrow x\in\varnothing\)
Đúng 2
Bình luận (0)
Giải giúp mình bài này với ạ giải câu c chi tiết xíu giúp mình với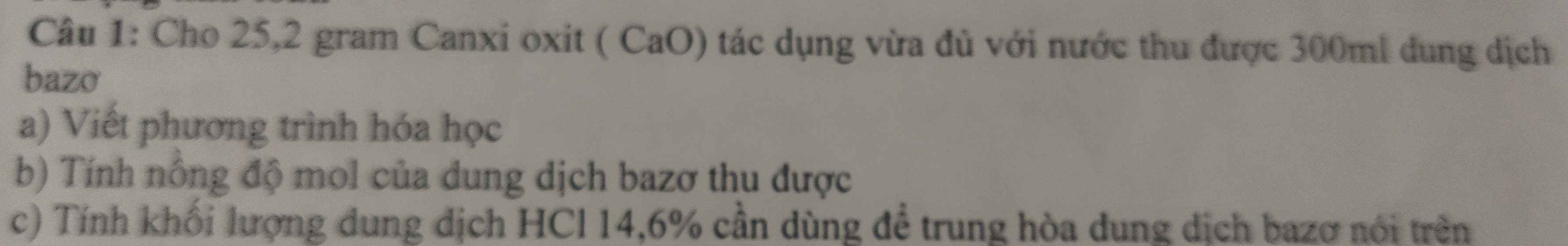
Giải giúp mình câu c ạ
Mọi người giúp em câu d hình với ạ. Câu a, b, c em giải được rồi.Lời giải câu a,b,c của em:
Đọc tiếp

Mọi người giúp em câu d hình với ạ. Câu a, b, c em giải được rồi.
Lời giải câu a,b,c của em:
Gọi giao điểm AE và BP là F;
Gọi giao điểm QD và AB là H;
Gọi kéo dài AD cắt BF tại P'
Dễ cm M là trung điểm AC
Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)
Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\)
\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)
Mà CM=AM (vì M là tđ AC)
\(\Rightarrow QD=DH\)
Dễ cm P là trung điểm BF
Xét \(\Delta ABP'\) có DH//BP'
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)
Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)
Mà DH=QD (cmt)
\(\Rightarrow BP'=FP'\)
\(\Rightarrow\)P' là trung điểm BF
\(\Rightarrow P\equiv P'\)
\(\Rightarrow A,D,P\) thẳng hàng
Đúng 0
Bình luận (0)

giúp e giải câu Phần" C. Grammar" thôi ạ. e cám ơn ạ
 giải giúp em câu c với ạ
giải giúp em câu c với ạ
Giải giúp e câu c với ạ
c)
Góc OQN= góc NAB
=> Tứ giác AONQ nội tiếp
Kết hợp câu a suy ra 5 điểm A, O, N, Q, P cùng nằm trên một đường tròn.
Lại có: góc ONP = góc OAP = 90°
=> ON vuông góc NP
=> PN là tiếp tuyến của đường tròn (O).
Đúng 0
Bình luận (0)




























