. Cho y = \(\frac{x^2cosa-2x+cosa}{x^2-2xcosa+1}\) (0<a<pi)
. CMR: -1 <= y <= 1 với mọi x

Những câu hỏi liên quan
Chứng minh các đẳng thức sau:
a.frac{1+sin^2x}{1-sin^{2^{ }}x}1+2tan^2x
b.frac{sin^3a-cos^3a}{sina-cosa}-sina.cosa1
c.frac{1+cosx+cos2x+cos3x}{2cos^2x+cosx-1}2cosx
e.frac{1-2sin^2a}{cosa+sina}+frac{2cos^2a-1}{cosa-sina}2cosa
d.frac{1-cosx+cos2x}{sin2x-sinx}cotx
MỌI NGƯỜI GIÚP MÌNH VỚI .MÌNH CẢM ƠN RẤT NHIỀU
Đọc tiếp
Chứng minh các đẳng thức sau:
a.\(\frac{1+sin^2x}{1-sin^{2^{ }}x}=1+2tan^2x\)
b.\(\frac{sin^3a-cos^3a}{sina-cosa}-sina.cosa=1\)
c.\(\frac{1+cosx+cos2x+cos3x}{2cos^2x+cosx-1}=2cosx\)
e.\(\frac{1-2sin^2a}{cosa+sina}+\frac{2cos^2a-1}{cosa-sina}=2cosa\)
d.\(\frac{1-cosx+cos2x}{sin2x-sinx}=cotx\)
MỌI NGƯỜI GIÚP MÌNH VỚI .MÌNH CẢM ƠN RẤT NHIỀU
\(\frac{1+sin^2x}{1-sin^2x}=\frac{1+sin^2x}{cos^2x}=\frac{1}{cos^2x}+\frac{sin^2x}{cos^2x}=1+tan^2x+tan^2x=1+2tan^2x\)
\(\frac{sin^3a-cos^3a}{sina-cosa}-sina.cosa=\frac{\left(sina-cosa\right)\left(sin^2a+cos^2a+sina.cosa\right)}{sina-cosa}-sina.cosa\)
\(=sin^2a+cos^2a+sina.cosa-sina.cosa=1\)
\(\frac{1+cos2x+cosx+cos3x}{2cos^2x-1+cosx}=\frac{1+2cos^2x-1+2cosx.cos2x}{cos2x+cosx}=\frac{2cosx\left(cosx+cos2x\right)}{cos2x+cosx}=2cosx\)
\(\frac{1-2sin^2a}{cosa+sina}+\frac{2cos^2a-1}{cosa-sina}=\frac{cos^2a-sin^2a}{cosa+sina}+\frac{cos^2a-sin^2a}{cosa-sina}\)
\(=\frac{\left(cosa+sina\right)\left(cosa-sina\right)}{cosa+sina}+\frac{\left(cosa+sina\right)\left(cosa-sina\right)}{cosa-sina}=cosa-sina+cosa+sina=2cosa\)
\(\frac{1-cosx+cos2x}{sin2x-sinx}=\frac{1-cosx+2cos^2x-1}{2sinx.cosx-sinx}=\frac{cosx\left(2cosx-1\right)}{sinx\left(2cosx-1\right)}=\frac{cosx}{sinx}=cotx\)
Đúng 0
Bình luận (0)
Cho cosa=\(\frac{1}{3}\)tính giá trị của biểu thức:\(B=\frac{sina-3cosa}{sina+2cosa}\)
Có \(\sin^2a+\cos^2a=1\)\(\Leftrightarrow\sin^2a=1-\cos^2a=1-\left(\frac{1}{3}\right)^2=\frac{8}{9}\)
\(\Leftrightarrow\sin a=\frac{\sqrt{8}}{3}\)
Xét \(B=\frac{\sin a-3\cos a}{\sin a+2\cos a}=\frac{\frac{\sqrt{8}}{3}-3\cdot\frac{1}{3}}{\frac{\sqrt{8}}{3}+2\cdot\frac{1}{3}}=\frac{7-5\sqrt{2}}{2}\)
Bài 1 CM các đẳng thức sau:
a, 1+ sin2a / sina + cosa - 1-tan ²a/2 / 1+ tan ²a/2 sina
b, cota - tana 2cot2a
c, 1+ cosa +cos2a + cos3a/ 2cos²a + cosa-1 2cosa
d, sin²a / sina- cosa - sina + cosa / tan²a sina + cosa
e, sin²a - cos²(a-b ) + 2coscosb ×cos(a-b) cos2a
f, cos²a - 2sina × ( 1-sina ) × cosa +( 1 + sina) × cosa - 2×(1+sina ) / 1- sina cosa
Bài 2 CM các đẳng thức sau ko phụ thuộc vào x
a, A sin⁶x + cos⁶x - 1 / sin⁴x + cos ⁴x -1
b, B ( 2sin ⁶x - 3sin ⁴x - 4...
Đọc tiếp
Bài 1 CM các đẳng thức sau:
a, 1+ sin2a / sina + cosa - 1-tan ²a/2 / 1+ tan ²a/2 = sina
b, cota - tana = 2cot2a
c, 1+ cosa +cos2a + cos3a/ 2cos²a + cosa-1 = 2cosa
d, sin²a / sina- cosa - sina + cosa / tan²a = sina + cosa
e, sin²a - cos²(a-b ) + 2coscosb ×cos(a-b) = cos2a
f, cos²a - 2sina × ( 1-sina ) × cosa +( 1 + sina) × cosa - 2×(1+sina ) / 1- sina = cosa
Bài 2 CM các đẳng thức sau ko phụ thuộc vào x
a, A= sin⁶x + cos⁶x - 1 / sin⁴x + cos ⁴x -1
b, B = ( 2sin ⁶x - 3sin ⁴x - 4sin²x ) +( 2cos⁶x - 3 cos⁴x- 4cos⁴x
c, C= sin⁴x + 3cos⁴x -1 / sin⁶x + cos⁶x + 3cos⁴x-1
Giải giúp tớ 2 bài này vs tớ cảm ơn nhìu
Cho \(tana=3\). Tính A = \(\frac{sina+2cosa}{sina-cosa}\)
tana = sina/cosa = 2 => sina = 2cosa
Thay sina = 2cosa vào biểu thức, ta có:
(sina + cosa)/(sina - cosa) = (2cosa + cosa)/(2cosa - cosa) = 3cosa/cosa = 3
Kết luận: (sina + cosa)/(sina - cosa) = 3
P/s: Bài này tui làm rồi
Đúng 0
Bình luận (1)
Ai biết làm thì trả lời hộ mình với, cảm ơn rất nhiều ! Xin lỗi vì viết câu trả lời không liên quan, thật lòng xin lỗi !
Đúng 0
Bình luận (0)
bạn ơi mình ghi \(tana\)=3 mà :[ sao bạn ghi là = 2 lúc đầu z
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho góc a thỏa mãn
π
a
3
π
2
và sina - 2cosa 1. Tính A 2tana- cosa A. 6 B.
1
6
C. 2 D.
1
2
Đọc tiếp
Cho góc a thỏa mãn π < a < 3 π 2 và sina - 2cosa = 1. Tính A = 2tana- cosa
A. 6
B. 1 6
C. 2
D. 1 2
Vì π < a < 3 π 2 nên sina < 0; cosa < 0. Ta có
sin α - 2 cos α = 1 sin 2 α + cos 2 α = 1 ⇒ 1 + 2 cos α 2 + cos 2 α = 1 ⇒ 5 cos 2 α + 4 cos α = 0 ⇒ cos α = - 4 5
Suy ra α = - 1 - cos 2 α = - 3 5 ; tan α = 3 4 ; c o t α = 4 3 . Vậy A = 2tana - cota = 2 . 3 4 - 4 3 = 1 6
Đáp án B
Đúng 0
Bình luận (0)
biết cosa= \(\dfrac{3}{4}\)
tính \(\dfrac{2cosa^2+1}{sina+cosa}+tana=...\)
giúp mình với
Cho hàm số \(y=\frac{1}{3}x^3-\frac{1}{2}\left(sina+cosa\right)x^2+\frac{3}{4}xsin2a\)Tìm a để y đồng biến trên R
lớp 8 chưa học lượng giác đâu bn
Mình quên mất. Đng học lp 8 nhưng học trc chương trình nên quên sửa lớp luôn
Ta có \(y'=x^2-\left(sina+cosa\right)x+\frac{3}{4}sin2a\)
Để y đồng biến trên R thì \(y'\ge0,\forall x\inℝ\)
\(\Leftrightarrow\Delta\le0\)
\(\Leftrightarrow\left(sina=cosa\right)^2-3sin2a\le0\)
\(\Leftrightarrow1-2sin2a\le0\)
\(\Leftrightarrow sin2a\ge\frac{1}{2}\Leftrightarrow\frac{\eta}{6}+k2\eta\le2a\le\frac{5\eta}{6}+k2\eta\)
\(\Leftrightarrow k\eta+\frac{\eta}{12}\le a\le\frac{5\eta}{12}+k\eta.\)
Mọi người giúp em giải bài này ạ, em cảm ơn
Bài 1: Rút gọn biểu thức:
Afrac{sin2x+sin x}{1+cos2x+cos x}
Bcotaleft(frac{1+sin^2a}{cos a}-cosaright)
Cfrac{1+cos x+cos2x+cos3x}{2cos^2x+cos x-1}
Dfrac{2cosleft(frac{pi}{2}-xright)cdotsinleft(frac{pi}{2}+xright)cdottanleft(pi-xright)}{cotleft(frac{pi}{2}+xright)cdotsinleft(pi-xright)}-2cos x
Ecos^2xcdotcot^2x+3cos^2x-cot^2x+2sin^2x
Ffrac{sin^2x+sin^2xtan^2x}{cos^2x+cos^2xtan^2x}
Gfrac{1+cos2a-cosa}{2sina-sina}
Hsin^{^{ }4}left(frac{pi}{2}+alp...
Đọc tiếp
Mọi người giúp em giải bài này ạ, em cảm ơn
Bài 1: Rút gọn biểu thức:
A=\(\frac{\sin2x+\sin x}{1+\cos2x+\cos x}\)
B=\(cota\left(\frac{1+\sin^2a}{\cos a}-cosa\right)\)
C=\(\frac{1+\cos x+\cos2x+\cos3x}{2\cos^2x+\cos x-1}\)
D=\(\frac{2\cos\left(\frac{\pi}{2}-x\right)\cdot\sin\left(\frac{\pi}{2}+x\right)\cdot\tan\left(\pi-x\right)}{\cot\left(\frac{\pi}{2}+x\right)\cdot\sin\left(\pi-x\right)}-2\cos x\)
E=\(\cos^2x\cdot\cot^2x+3\cos^2x-\cot^2x+2\sin^2x\)
\(F=\frac{\sin^2x+\sin^2x\tan^2x}{\cos^2x+\cos^2x\tan^2x}\)
\(G=\frac{1+cos2a-cosa}{2sina-sina}\)
H=\(sin^{^{ }4}\left(\frac{\pi}{2}+\alpha\right)-cos^4\left(\frac{3\pi}{2}-\alpha\right)+1\)
Bài 2: chứng minh
a) cho \(\Delta ABCchứngminhsin\frac{A+B}{2}=cos\frac{C}{2}\)
b) chứng minh biểu thức sau độc lập với biến x:
A=\(cosx+cos\left(x+\frac{2\pi}{3}\right)+cos\left(x+\frac{4\pi}{3}\right)\)
c)cho \(\Delta\) ABC chứng minh : sin A+sin B+ sin C= \(4cos\frac{A}{2}cos\frac{B}{2}cos\frac{C}{2}\)
d)CMR: \(\frac{cos2a}{1+sin2a}=\frac{cosa-sina}{cosa+sina}\)
e) CMR:\(E=\frac{sin\alpha+cos\alpha}{cos^3\alpha}=1+tan\alpha+tan^2\alpha+tan^3\alpha\)
f) CMR \(\Delta\)ABC cân khi và chỉ khi \(sinB=2cosAsinC\)
g) CM: \(\frac{1-cosx+cos2x}{sin2x-sinx}=cotx\)
h)CM: \(\left(cos3x-cosx\right)^2+\left(sin3x-sinx\right)^2=4sin^2x\)
k) CMR trong tam giac ABC ta có: \(sin2A+sin2B+sin2C=4sinA\cdot sinB\cdot sinC\)
Bài 3: giải bất phương trình:
a)\(\frac{\left(1-3x\right)\left(2x^2+1\right)}{-2x^2-3x+5}>0\)
b)\(\frac{2x+1}{\left(x-1\right)\left(x+2\right)}\ge0\)
c)\(\frac{\left(3x-2\right)\left(x^2-9\right)}{x^2-4x+4}\le0\)
d)\(\frac{\left(2x^2+3x\right)\left(3-2x\right)}{1-x^2}\ge0\)
e)\(\frac{\left(x^2+2x+1\right)\left(x-1\right)}{3-x^2}\)
f)\(\frac{2x+1}{-x^2+x+6}\ge0\)
\(A=\frac{2sinx.cosx+sinx}{1+2cos^2x-1+cosx}=\frac{sinx\left(2cosx+1\right)}{cosx\left(2cosx+1\right)}=\frac{sinx}{cosx}=tanx\)
\(B=\frac{cosa}{sina}\left(\frac{1+sin^2a}{cosa}-cosa\right)=\frac{cosa}{sina}\left(\frac{1+sin^2a-cos^2a}{cosa}\right)=\frac{cosa}{sina}.\frac{2sin^2a}{cosa}=2sina\)
\(C=\frac{1+cos2x+cosx+cos3x}{2cos^2x-1+cosx}=\frac{1+2cos^2x-1+2cos2x.cosx}{cos2x+cosx}=\frac{2cosx\left(cosx+cos2x\right)}{cos2x+cosx}=2cosx\)
\(D=\frac{2sinx.cosx.\left(-tanx\right)}{-tanx.sinx}-2cosx=2cosx-2cosx=0\)
Đúng 0
Bình luận (1)
\(E=cos^2x.cot^2x-cot^2x+cos^2x+2cos^2x+2sin^2x\)
\(E=cot^2x\left(cos^2x-1\right)+cos^2x+2=\frac{cos^2x}{sin^2x}\left(-sin^2x\right)+cos^2x+2=2\)
\(F=\frac{sin^2x\left(1+tan^2x\right)}{cos^2x\left(1+tan^2x\right)}=\frac{sin^2x}{cos^2x}=tan^2x\)
Câu G mẫu số có gì đó sai sai, sao lại là \(2sina-sina?\)
\(H=sin^4\left(\frac{\pi}{2}+a\right)-cos^4\left(\frac{3\pi}{2}-a\right)+1=cos^4a-sin^4a+1\)
\(=\left(cos^2a-sin^2a\right)\left(cos^2a+sin^2a\right)+1=cos^2a-\left(1-cos^2a\right)+1=2cos^2a\)
Đúng 0
Bình luận (1)
Bài 2:
\(sin\frac{A+B}{2}=sin\left(\frac{180^0-C}{2}\right)=sin\left(90^0-\frac{C}{2}\right)=cos\frac{C}{2}\)
b/
\(A=cosx+cos\left(x+\frac{2\pi}{3}\right)+cos\left(x+\frac{4\pi}{3}\right)=cosx+2cos\left(x+\pi\right).cos\frac{\pi}{3}\)
\(=cosx-2cosx.\frac{1}{2}=0\)
c/
\(sinA+sinB+sinC=2sin\frac{A+B}{2}cos\frac{A-B}{2}+2sin\frac{C}{2}cos\frac{C}{2}=2cos\frac{C}{2}.cos\frac{A-B}{2}+2sin\frac{C}{2}cos\frac{C}{2}\)
\(=2cos\frac{C}{2}\left(cos\frac{A-B}{2}+sin\frac{C}{2}\right)=2cos\frac{C}{2}\left(cos\frac{A-B}{2}+cos\frac{A+B}{2}\right)=4cos\frac{A}{2}cos\frac{B}{2}cos\frac{C}{2}\)
d/ \(\frac{cos2a}{1+sin2a}=\frac{cos^2a-sin^2a}{cos^2a+sin^2a+2sina.cosa}=\frac{\left(cosa-sina\right)\left(cosa+sina\right)}{\left(cosa+sina\right)^2}=\frac{cosa-sina}{cosa+sina}\)
e/
\(E=\frac{sina+cosa}{cos^3a}=\frac{1}{cos^2a}\left(tana+1\right)=\left(1+tan^2a\right)\left(tana+1\right)\)
\(E=tan^3a+tan^2a+tana+1\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm a ∈ (0; 2 π ) để hàm số sau đồng biến trên khoảng (1; + ∞ ).
y = 1 3 x 3 - 1 2 (1 + cosa) x 2 + 2x cosa + 1
Tập xác định: D = R; y′ = x 2 − (1 + 2cosa)x + 2cosa
y′= 0 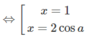
Vì y’ < 0 ở ngoài khoảng nghiệm nên để hàm số đồng biến với mọi x > 1 thì 2cosa ≤ 1
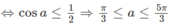
(vì a ∈ (0; 2 π ).
Đúng 0
Bình luận (0)

















