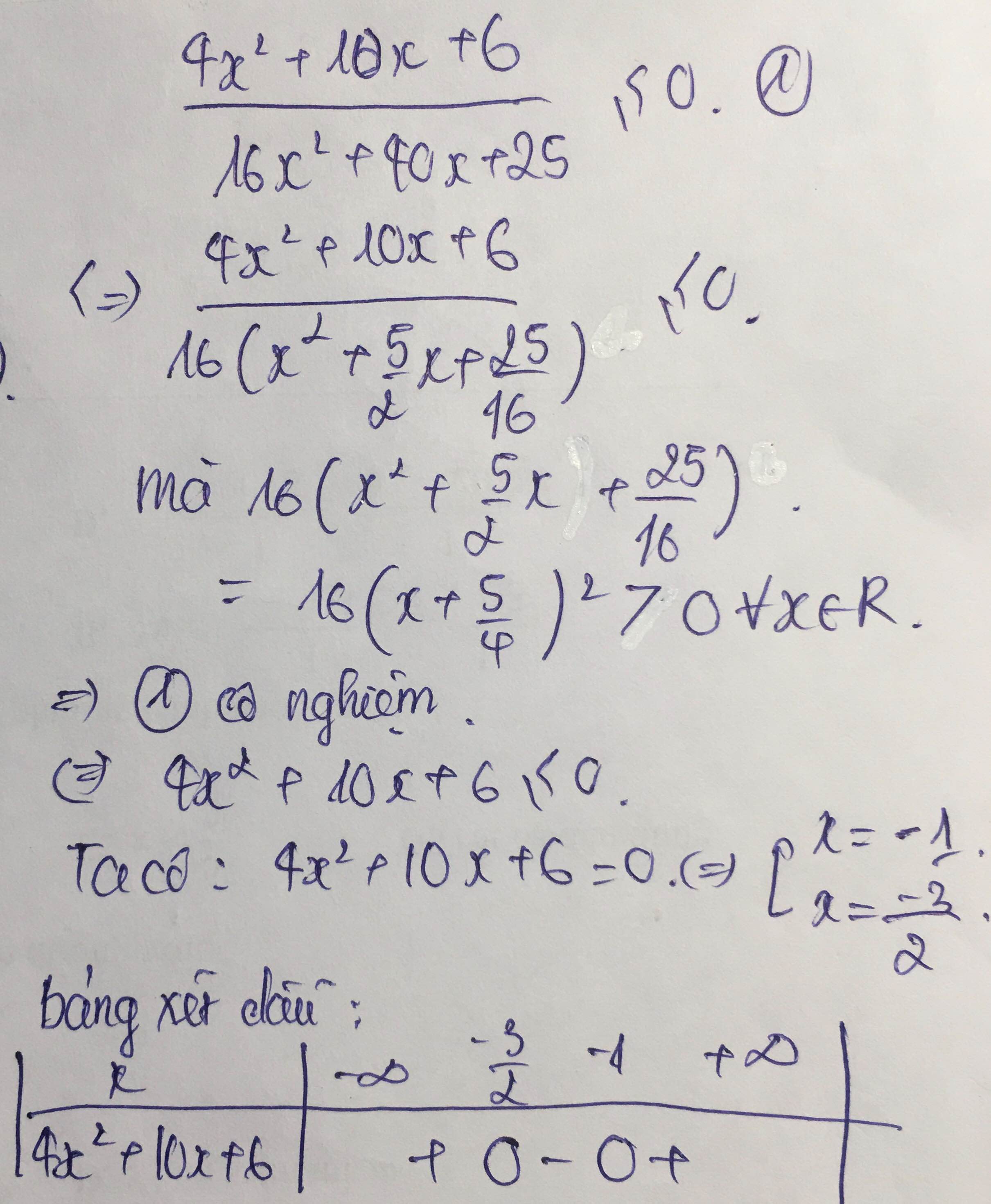\(\Leftrightarrow5x=20-5\\ \Leftrightarrow5x=15\\ \Leftrightarrow x=3\)

a: \(=20x^2-25x-20x^2+24x-30=-x-30\)

b: \(\Leftrightarrow12x-6x^2+6x^2-15x=12\)

=>-3x=12

hay x=-4

a ) 

\(5x\left(4x-5\right)-4x\left(5x-6\right)=30\)

\(\Rightarrow20x^2-25x-20x^2+24x=30\)

\(\Rightarrow-x=30\)

\(\Rightarrow x=-30\)

Vậy ...

b ) 

\(2x\left(6-3x\right)+3x\left(2x-5\right)=12\)

\(\Rightarrow12x-6x^2+6x^2-15x=12\)

\(\Rightarrow-3x=12\)

\(\Rightarrow x=-4\)

Vậy ...

a) \(5x\left(4x-5\right)-4x\left(5x-6\right)-30\)

\(\Rightarrow20x^2-25x-20x^2+24x=30\)

\(\Rightarrow-1x=30\)

\(\Rightarrow x=-30\)

Vậy x = -30

b) \(2x\left(6-3x\right)+3x\left(2x-5\right)=12\)

\(\Rightarrow12x-6x^2+6x^2-15x=12\)

\(\Rightarrow-3x=12\)

\(\Rightarrow x=-4\)

Vậy x = -4

cảm ơn các bạn nếu đc các bạn có thể trả lời hết số câu hỏi tớ vừa hỏi có đc ko ạ

b: \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-4\end{matrix}\right.\)

a) \(3x\cdot\left(12x-4\right)-9x\cdot\left(4x-3\right)=30\)

\(\Leftrightarrow36x^2-12x-36x^2+27x=30\)

\(\Leftrightarrow15x=30\)

\(\Leftrightarrow x=\dfrac{30}{15}\)

\(\Leftrightarrow x=2\)

b) \(\left(2x+1\right)-5\left(x-2\right)=10\)

\(\Leftrightarrow2x+1-5x+10=10\)

\(\Leftrightarrow-3x+11=10\)

\(\Leftrightarrow-3x=10-11\)

\(\Leftrightarrow-3x=-1\)

\(\Leftrightarrow x=\dfrac{1}{3}\)

ĐKXĐ: \(x\ge-1\)

\(3x^2-2x-2=\dfrac{6}{\sqrt{30}}\sqrt{\left(x+1\right)\left(x^2+2x+2\right)}\)

\(\Leftrightarrow3\left(x^2+2x+2\right)-8\left(x+1\right)=\dfrac{6}{\sqrt{30}}\sqrt{\left(x+1\right)\left(x^2+2x+2\right)}\)

Đặt \(\left\{{}\begin{matrix}\sqrt{x^2+2x+2}=a>0\\\sqrt{x+1}=b\ge0\end{matrix}\right.\)

\(\Rightarrow3a^2-8b^2-\dfrac{6}{\sqrt{30}}ab=0\)

\(\Leftrightarrow\left(3a-\sqrt{30}b\right)\left(a+\dfrac{4\sqrt{30}}{15}b\right)=0\)

\(\Leftrightarrow3a=\sqrt{30}b\)

\(\Leftrightarrow3\sqrt{x^2+2x+2}=\sqrt{30\left(x+1\right)}\)

\(\Leftrightarrow9\left(x^2+2x+2\right)=30\left(x+1\right)\)

\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{2}{3}\\x=2\end{matrix}\right.\)