trong mặt phẳng tọa độ Oxy , cho đường thẳng (Δ) : ax + by + c = 0 và điểm I(x0 ; y0) . Phép đối xứng tâm ĐI biến đường thẳng Δ thành đường thẳng Δ' . Viết phương trình của Δ'.

Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0; 1; 1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S. A. 36π B.
36
2
π
C.
18
2
π
D. 18π
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0; 1; 1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S.
A. 36π
B.
36
2
π
C. 18 2 π
D. 18π
Trong mặt phẳng tọa độ Oxy, cho điểm A(2;1) và đường thẳng Δ: x-2y+5=0. Điểm M thuộc đường thẳng Δ sao cho AM = \(\sqrt{10}\) là:
giúp tớ nhé các bạn
Gọi `M(2y-5;y) in \Delta`
Ta có: `AM=\sqrt{10}`
`<=>|\vec{AM}|=\sqrt{10}`
`<=>\sqrt{(2y-5-2)^2+(y-1)^2}=\sqrt{10}`
`<=>4y^2-28y+49+y^2-2y+1=10`
`<=>[(y=4),(y=2):}`
`=>[(M(3;4)),(M(-1;2)):}`
Đúng 2
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng
∆
:
x
-
1
2
y
-
1
1
z
-
1
-
1
và mặt phẳng
P
: x+y+z-30. Gọi d là đường thẳng nằm trong...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng ∆ : x - 1 2 = y - 1 1 = z - 1 - 1 và mặt phẳng P : x+y+z-3=0. Gọi d là đường thẳng nằm trong (P), đi qua giao điểm của Δ và (P), đồng thời vuông góc với Δ. Giao điểm của đường thẳng d với mặt phẳng tọa độ (Oxy) là
A. M(2;2;0)
B. M(-3;2;0)
C. M(-1;4;0)
D. M(-3;4;0)
Trong mặt phẳng tọa độ Oxy , cho điểm I (-1;2) và đường thẳng d: x+3y+5 0 a) Viết phương trình đường tròn (C) có tâm I và đường kính bằng 4sqrt{5}.Tìm tọa độ các giao điểm của d và (C)b) Viết phương trình đường thằng Δ vuông góc với d và căt (C) tại hai điểm phân biệt A,B sao cho tam giác IAB tù và có diện tích bằng 5sqrt{3}
Đọc tiếp
Trong mặt phẳng tọa độ Oxy , cho điểm I (-1;2) và đường thẳng d: x+3y+5 = 0
a) Viết phương trình đường tròn (C) có tâm I và đường kính bằng \(4\sqrt{5}\).Tìm tọa độ các giao điểm của d và (C)
b) Viết phương trình đường thằng Δ vuông góc với d và căt (C) tại hai điểm phân biệt A,B sao cho tam giác IAB tù và có diện tích bằng \(5\sqrt{3}\)
a, Bán kính: \(R=2\sqrt{5}\)
Phương trình đường tròn: \(\left(x+1\right)^2+\left(y-2\right)^2=20\)
Giao điểm của d và (C) có tọa độ là nghiệm hệ:
\(\left\{{}\begin{matrix}\left(x+1\right)^2+\left(y-2\right)^2=20\\x+3y+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(3y+4\right)^2+\left(y-2\right)^2=20\\x=-3y-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10y^2+20y=0\\x=-3y-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}y=0\\x=-5\end{matrix}\right.\\\left\{{}\begin{matrix}y=-2\\x=1\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}M=\left(0;-5\right)\\N=\left(-2;1\right)\end{matrix}\right.\) là các giao điểm
b, Gọi H là trung điểm AB.
Đường thẳng \(\Delta\) vuông góc với d nên có phương trình dạng: \(3x-y+m=0\left(m\in R\right)\)
Ta có: \(S_{IAB}=\dfrac{1}{2}.R^2.sinAIB=10.sinAIB=5\sqrt{3}\)
\(\Rightarrow sinAIB=\dfrac{\sqrt{3}}{2}\)
Mà tam giác ABC tù nên \(\widehat{AIB}=120^o\)
\(\Rightarrow\widehat{HBI}=30^o\)
Khi đó:
\(IH=d\left(I;\Delta\right)\)
\(\Leftrightarrow R.sinHBI=\dfrac{\left|-3-2+m\right|}{\sqrt{10}}\)
\(\Leftrightarrow2\sqrt{5}.sin30^o=\dfrac{\left|m-5\right|}{\sqrt{10}}\)
\(\Leftrightarrow m=5\pm5\sqrt{2}\)
\(\Rightarrow\left[{}\begin{matrix}\Delta:3x-y+5+5\sqrt{2}=0\\\Delta:3x-y+5-5\sqrt{2}=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho đường thẳng d: \(2x+y-3=0\) và đường thẳng Δ:\(4x+2y-1=0\). Tập hợp các điểm cách đều đường thẳng d và Δ nằm trên đường thẳng l có phương trình \(ax+by+1=0\) với a, b ∈ R. Tính a+b
Ta có : Đường thẳng I cách đều 2 đường thẳng d và denta
\(\Rightarrow\dfrac{\left|2x+y-3\right|}{\sqrt{5}}=\dfrac{\left|4x+2y-1\right|}{2\sqrt{5}}\)
\(\Rightarrow2\left|2x+y-3\right|=\left|4x+2y-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+2y-6=4x+2y-1\\4x+2y-6=-4x-2y+1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-6=1\left(L\right)\\8x+4y-7=0\end{matrix}\right.\)
\(\Leftrightarrow-\dfrac{8}{7}+\left(-\dfrac{4}{7}\right)+1=0\)
\(\Rightarrow a+b=-\dfrac{8}{7}-\dfrac{4}{7}=-\dfrac{12}{7}\)
Vậy ..
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S. A. 36π B. 36
2
π C. 18
2
π D. 18 π
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S.
A. 36π
B. 36 2 π
C. 18 2 π
D. 18 π
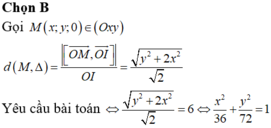
Vậy quỹ tích M trên (Oxy) là hình Elip với
![]()
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I(0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S A.
36
2
π
B.
18
π
C.
36
π
D.
18...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I(0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S
A. 36 2 π
B. 18 π
C. 36 π
D. 18 2 π
Đáp án A
Phương pháp:
Tính khoảng cách từ 1 điểm M đến đường thẳng Δ: 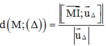 với
u
△
→
là 1 VTCP của Δ và I
∈
Δ là 1 điểm bất kì
với
u
△
→
là 1 VTCP của Δ và I
∈
Δ là 1 điểm bất kì
Cách giải: Đường thẳng Δ nhận ![]() là 1 VTCP
là 1 VTCP
Gọi M(a;b;0)
∈
(Oxy) => 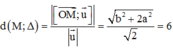
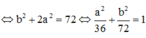
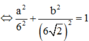
Như vậy tập hợp các điểm M là elip có phương trình 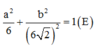
![]()
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy , cho điểm I (-1;2) và đường thẳng d: x+3y+5 0 a) Viết phương trình đường tròn (C) có tâm I và đường kính bằng 4√545.Tìm tọa độ các giao điểm của d và (C)b) Viết phương trình đường thằng Δ vuông góc với d và căt (C) tại hai điểm phân biệt A,B sao cho tam giác IAB tù và có diện tích bằng 5√353
Đọc tiếp
Trong mặt phẳng tọa độ Oxy , cho điểm I (-1;2) và đường thẳng d: x+3y+5 = 0
a) Viết phương trình đường tròn (C) có tâm I và đường kính bằng 4√545.Tìm tọa độ các giao điểm của d và (C)
b) Viết phương trình đường thằng Δ vuông góc với d và căt (C) tại hai điểm phân biệt A,B sao cho tam giác IAB tù và có diện tích bằng 5√353
a, Bán kính: \(R=2\sqrt{545}\)
Phương trình đường tròn: \(\left(x+1\right)^2+\left(y-2\right)^2=2180\)
Giao điểm của \(\left(C\right);\left(d\right)\) có tọa độ là nghiệm hệ:
\(\left\{{}\begin{matrix}x+3y+5=0\\\left(x+1\right)^2+\left(y-2\right)^2=2180\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-3y-5\\\left(-3y-4\right)^2+\left(y-2\right)^2=2180\end{matrix}\right.\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ Oxy cho đồ thị hàm số y=ax là đường thẳng OM với M(-3;2).Điểm N(x0;y0)thuộc đồ thị hàm số trên.Tính x0-3/y0+2














