Đáp án A
Phương pháp:
Tính khoảng cách từ 1 điểm M đến đường thẳng Δ: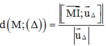 
với
u
△
→
là 1 VTCP của Δ và I
∈
Δ là 1 điểm bất kì
Cách giải: Đường thẳng Δ nhận 
là 1 VTCP
Gọi M(a;b;0)
∈
(Oxy) =>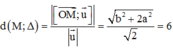 
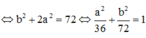
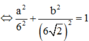
Như vậy tập hợp các điểm M là elip có phương trình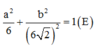 
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : x + y − 4 z = 0 , đường thẳng d : x − 1 2 = y + 1 − 1 = z − 3 1 và điểm A 1 ; 3 ; 1 thuộc mặt phẳng P . Gọi Δ là đường thẳng đi qua A, nằm trong mặt phẳng (P) và cách d một khoảng cách lớn nhất. Gọi u → = a ; b ; 1 là một VTCP của đường thẳng Δ . Tính a + 2 b .
A. a + 2 b = − 3.
B. a + 2 b = 0.
C. a + 2 b = 4.
D. a + 2 b = 7.
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng ∆ : x - 1 2 = y - 1 1 = z - 1 - 1 và mặt phẳng P : x+y+z-3=0. Gọi d là đường thẳng nằm trong (P), đi qua giao điểm của Δ và (P), đồng thời vuông góc với Δ. Giao điểm của đường thẳng d với mặt phẳng tọa độ (Oxy) là
A. M(2;2;0)
B. M(-3;2;0)
C. M(-1;4;0)
D. M(-3;4;0)
Trong không gian với hệ tọa độ Oxyz, cho đường cong (T) là tập hợp tâm của các mặt cầu (S) đi qua điểm A(1;1;1) đồng thời tiếp xúc với hai mặt phẳng α : x + y + z − 6 = 0 và β : x + y + z + 6 = 0 . Diện tích hình phẳng giới hạn bởi đường cong (T) bằng
A. 3 5
B. 9 π
C. 48 π
D. 45 π
Trong không gian Oxyz, đường thẳng Δ qua điểm M(1−2m;2+ m;1) và vuông góc với mặt phẳng (Oxy) sao cho khoảng cách từ gốc toạ độ O đến đường thẳng Δ nhỏ nhất có phương trình là
A. x = 1 y = 2 z = 1 + t
B. x = 1 + t y = 2 + t z = 1
C. x = 5 y = 0 z = 1 + t
D. x = 3 y = 1 z = 1 + t
Trong không gian tọa độ Oxyz, cho điểm A 1 ; 0 ; 2 , B 3 ; 1 ; 4 , C 3 ; − 2 ; 1 . Gọi Δ là đường thẳng đi qua A và vuông góc với mặt phẳng (ABC). Tìm điểm S ∈ Δ sao cho mặt cầu ngoại tiếp hình chóp S.ABC có bán kính R = 3 2 .
A. S 4 − 3 π 3 ; 2 − 6 π 3 ; 4 + 6 π 3 hoặc S 4 + 3 π 3 ; 2 + 6 π 3 ; 4 − 6 π 3
B. S 4 + 3 π 3 ; 2 − 6 π 3 ; 4 + 6 π 3 hoặc S 4 − 3 π 3 ; 2 + 6 π 3 ; 4 − 6 π 3
C. S 4 + 3 π 3 ; 2 + 6 π 3 ; 4 − 6 π 3 hoặc S 4 − 3 π 3 ; 2 − 6 π 3 ; 4 + 6 π 3
D. S 4 − 3 π 3 ; 2 + 6 π 3 ; 4 + 6 π 3 hoặc S 4 + 3 π 3 ; 2 − 6 π 3 ; 4 − 6 π 3
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;1;1) và mặt phẳng P : x + 2 y = 0 . Gọi Δ là đường thẳng đi qua A, song song với (P) và cách điểm B(-1;0;2) một khoảng ngắn nhất. Hỏi nhận vectơ nào dưới đây là vectơ chỉ phương.
A. u → = 6 ; 3 ; − 5
B. u → = 6 ; − 3 ; 5
C. u → = 6 ; 3 ; 5
D. u → = 6 ; − 3 ; − 5
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;0;-1) và mặt phẳng P : x + y - z - 3 = 0 . Gọi (S) là mặt cầu có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng 17 2 . Tính bán kính R của mặt cầu (S)
A. R = 3
B. R = 9
C. R = 1
D. R = 5
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;0;-1) và mặt phẳng P : x + y - z - 3 = 0 . Gọi (S) là mặt cầu có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng 17 2 . Tính bán kính R của mặt cầu (S).
A. R = 3
B. R = 9
C. R = 1
D. R = 5
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α): 2x+y-2z-2 = 0 và đường thẳng có phương trình d : x + a 1 = y + 2 2 = z + 3 2 và điểm A(1/2;1;1) Gọi ∆ là đường thẳng nằm trong mặt phẳng (α) , song song với d, đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng:
A. 7/3
B. 7/2
C. 21 2
D. 3/2
