Cho đường tròn (O) điểm A thuộc bán kính R, vẽ 2 dây AB; AC vuông góc vs nhau. Gọi M là trung điểm của AB, N là trung điểm của AC. Chwngsminh MN có độ dài ko đổi khi BÂC quay quanh điểm A

Những câu hỏi liên quan
cho đường tròn O bán kính R, dây AB cố định. Điểm M thuộc cung lớn AB. Gọi I là trung điểm của dây AB. Vẽ đường tròn tâm O' qua M tiếp xúc với AB tại A. Tia MI cắt đường tròn tâm o' tại N và cắt đường tròn tâm O tại C. cm NA song sonh với BC?
cho đường tròn O bán kính R, dây AB cố định. Điểm M thuộc cung lớn AB. Gọi I là trung điểm của dây AB. Vẽ đường tròn tâm O' qua M tiếp xúc với AB tại A. Tia MI cắt đường tròn tâm o' tại N và cắt đường tròn tâm O tại C. cm NA song sonh với BC?
Xét (O'): \(O'A\perp AB\) tại A và O'A là bán kính.
\(\Rightarrow\)AB là tiếp tuyến của (O') tại A.
\(\Rightarrow\widehat{NAB}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung AN.
Mặt khác \(\widehat{AMN}\) là góc nội tiếp chắn cung AN.
\(\Rightarrow\widehat{AMN}=\widehat{NAB}\left(1\right)\)
Xét (O): \(\widehat{AMC}=\widehat{ABC}\left(=\dfrac{1}{2}sđ\stackrel\frown{AC}\right)\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\widehat{NAB}=\widehat{ABC}\) nên AN//BC.
Đúng 2
Bình luận (0)
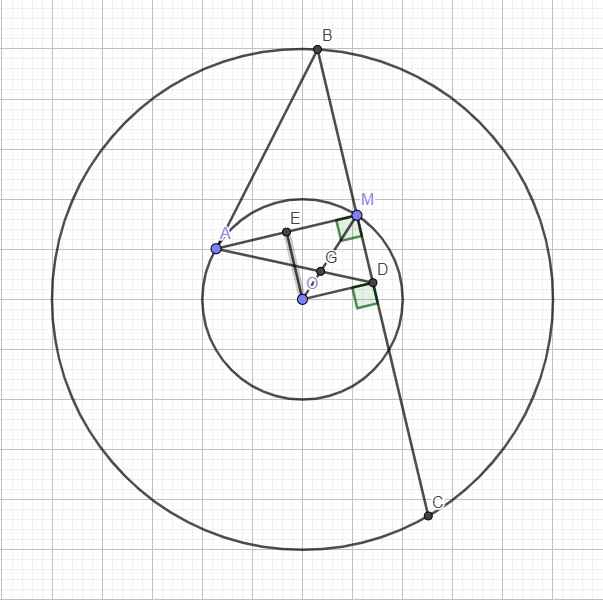
Cho 2 đường tròn đồng tâm O có bán kính R và r (R>r).A,M là 2 điểm thuộc đường tròn nhỏ (A di động,M cố định).Qua M vẽ dây BC của đường tròn lớn sao cho BC\(\perp\)AM.
a) Chứng minh tổng \(MA^2+MB^2+MC^2\) không phụ thuộc vào A
b) chứng minh trọng tâm G của tam giác ABC cố định
Cho 2 đường tròn đồng tâm O có bán kính R và r (R>r).A,M là 2 điểm thuộc đường tròn nhỏ (A di động,M cố định).Qua M vẽ dây BC của đường tròn lớn sao cho BC⊥⊥AM.
a) Chứng minh tổng \(MA^2+MB^2+MC^2\) không phụ thuộc vào A
b) chứng minh trọng tâm G của tam giác ABC cố định
a.
Gọi D là trung điểm BC \(\Rightarrow OD\perp BC\)
Gọi E là trung điểm AM \(\Rightarrow OE\perp AM\)
\(\Rightarrow\) Tứ giác OEMD là hình chữ nhật (có 3 góc vuông)
\(\Rightarrow MD=OE\) và \(ME=OD\)
\(MA^2+MB^2+MC^2=MA^2+\left(BD-MD\right)^2+\left(DC+MD\right)^2\)
\(=\left(2ME\right)^2+\left(BD-MD\right)^2+\left(BD+MD\right)^2\) (do \(BD=CD\))
\(=4ME^2+2BD^2+2MD^2\)
\(=2\left(ME^2+BD^2\right)+2\left(ME^2+MD^2\right)\)
\(=2\left(OD^2+BD^2\right)+2\left(OD^2+MD^2\right)\)
\(=2OB^2+2OM^2\)
\(=2R^2+2r^2\) cố định (đpcm)
b. Gọi G là giao điểm OM và AD
Theo c/m câu a ta có \(\left\{{}\begin{matrix}OD||AM\\OD=EM=\dfrac{1}{2}AM\end{matrix}\right.\)
Theo định lý Talet: \(\dfrac{DG}{AG}=\dfrac{OD}{AM}=\dfrac{OG}{GM}=\dfrac{1}{2}\Rightarrow\left\{{}\begin{matrix}AG=\dfrac{2}{3}AD\\OG=\dfrac{1}{3}OM\end{matrix}\right.\)
Do O, M cố định \(\Rightarrow\) G cố định
Mặt khác trong tam giác ABC do D là trung điểm AB \(\Rightarrow\) AD là trung tuyến
Mà \(AG=\dfrac{2}{3}AD\Rightarrow\) G là trọng tâm tam giác ABC
\(\Rightarrow\) Trọng tâm tam giác ABC cố định
Đúng 1
Bình luận (0)
Cho đường tròn (O) đường kính AB. Vẽ dây CD không qua tâm vuông góc với AB tại I (A thuộc cung nhỏ CD) biết CD=16cm ; IA=6cm. Tính bán kính của (O;R)
Xét (O) có
ΔACB nội tiếp
AB là đường kính
=>ΔACB vuông tại C
ΔOCD cân tại O
mà OI là đường cao
nên I là trung điểm của CD
=>IC=ID=CD/2=8cm
Xét ΔCAB vuông tại C cso CI là đường cao
nên CI^2=IA*IB
=>8^2=6*IB
=>IB=64/6=32/3(cm)
AB=IB+IA=32/3+6=50/3(cm)
=>R=50/3:2=25/3(cm)
Đúng 0
Bình luận (0)
Cho đường tròn tâm O, bán kính R. M là điểm nằm ngoài đường tròn. Vẽ tiếp tuyển MA của đường tròn (A là tiếp điểm). Vẽ đường kính AB của (O), MB cắt (O) tại C. Gọi D là trung điểm của dây BC. a) Chứng minh 4 điểm: M, A, O, D cùng nằm trên một đường tròn. b) Chứng minh 4Rẻ=BC BM
a: Xét tứ giác MAOD có
\(\widehat{MAO}+\widehat{ODM}=180^0\)
Do đó: MAOD là tứ giác nội tiếp
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính R,dây AB = R.căn 3 .Vẽ đường kính CD vuông góc AB(C thuộc cung AB lớn).Trên cung AC lấy M.Vẽ dây AN//CM.Tính MN
Cho đường tròn (O) có bán kính R và một điểm A sao cho OA2R, vẽ các tiếp tuyến AB, AC với (O) (B và C là các tiếp điểm). Vẽ đường kính BOD a)Chứng minh 4 điểm A,B,O,C cùng thuộc một đường tròn b)Chứng minh DC//OA c)Đường trung trực của BD cắt AC và BD lần lượt tại S và E. Chứng minh tứ giác OCEA là hình thang cân
Đọc tiếp
Cho đường tròn (O) có bán kính R và một điểm A sao cho OA=2R, vẽ các tiếp tuyến AB, AC với (O) (B và C là các tiếp điểm). Vẽ đường kính BOD a)Chứng minh 4 điểm A,B,O,C cùng thuộc một đường tròn b)Chứng minh DC//OA c)Đường trung trực của BD cắt AC và BD lần lượt tại S và E. Chứng minh tứ giác OCEA là hình thang cân
Bài IV (3,5 điểm) Cho nửa đường tròn tâm O, bán kính R, đường kính AB. Điểm C thuộc đoạn AB (C khác B;A). Trên cùng nửa mặt phẳng bờ AB có chứa nửa (O;R). Vẽ nửa đường tròn tâm I, đường kính AC và nửa đường tròn tâm J, đường kính BC. Qua C kẻ đường thẳng vuông góc với AB cắt (O;R) tại D. DA cắt nửa đường tròn tâm I tại M, DB cắt nửa đường tròn tâm J tại N 1) Chứng minh rằng: Tứ giác MDNC là hình chữ nhật2) Chứng minh rằng: Tứ giác AMNB nội tiếp.3) Chứng minh rằng: OD vuông góc MN4) Tì...
Đọc tiếp
Bài IV (3,5 điểm) Cho nửa đường tròn tâm O, bán kính R, đường kính AB. Điểm C thuộc đoạn AB (C khác B;A). Trên cùng nửa mặt phẳng bờ AB có chứa nửa (O;R). Vẽ nửa đường tròn tâm I, đường kính AC và nửa đường tròn tâm J, đường kính BC. Qua C kẻ đường thẳng vuông góc với AB cắt (O;R) tại D. DA cắt nửa đường tròn tâm I tại M, DB cắt nửa đường tròn tâm J tại N
1) Chứng minh rằng: Tứ giác MDNC là hình chữ nhật
2) Chứng minh rằng: Tứ giác AMNB nội tiếp.
3) Chứng minh rằng: OD vuông góc MN
4) Tìm vị trí của C trên AB để bán kính đường tròn ngoại tiếp tứ giác AMNB lớn nhất.