a.
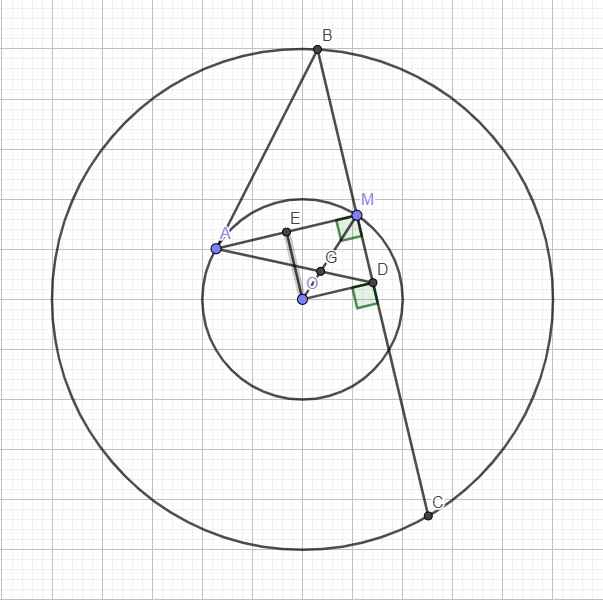
Gọi D là trung điểm BC \(\Rightarrow OD\perp BC\)
Gọi E là trung điểm AM \(\Rightarrow OE\perp AM\)
\(\Rightarrow\) Tứ giác OEMD là hình chữ nhật (có 3 góc vuông)
\(\Rightarrow MD=OE\) và \(ME=OD\)
\(MA^2+MB^2+MC^2=MA^2+\left(BD-MD\right)^2+\left(DC+MD\right)^2\)
\(=\left(2ME\right)^2+\left(BD-MD\right)^2+\left(BD+MD\right)^2\) (do \(BD=CD\))
\(=4ME^2+2BD^2+2MD^2\)
\(=2\left(ME^2+BD^2\right)+2\left(ME^2+MD^2\right)\)
\(=2\left(OD^2+BD^2\right)+2\left(OD^2+MD^2\right)\)
\(=2OB^2+2OM^2\)
\(=2R^2+2r^2\) cố định (đpcm)
b. Gọi G là giao điểm OM và AD
Theo c/m câu a ta có \(\left\{{}\begin{matrix}OD||AM\\OD=EM=\dfrac{1}{2}AM\end{matrix}\right.\)
Theo định lý Talet: \(\dfrac{DG}{AG}=\dfrac{OD}{AM}=\dfrac{OG}{GM}=\dfrac{1}{2}\Rightarrow\left\{{}\begin{matrix}AG=\dfrac{2}{3}AD\\OG=\dfrac{1}{3}OM\end{matrix}\right.\)
Do O, M cố định \(\Rightarrow\) G cố định
Mặt khác trong tam giác ABC do D là trung điểm AB \(\Rightarrow\) AD là trung tuyến
Mà \(AG=\dfrac{2}{3}AD\Rightarrow\) G là trọng tâm tam giác ABC
\(\Rightarrow\) Trọng tâm tam giác ABC cố định