Giá trị rút gọn của biểu thức là ...

Những câu hỏi liên quan
Rút gọn biểu thức sau, rồi tìm giá trị của x để giá trị của biểu thức rút gọn là 1 số dương:
\(\dfrac{8-2x}{x^2+x-20}\)
\(\dfrac{8-2x}{x^2+x-20}=-\dfrac{2\left(4-x\right)}{\left(4-x\right)\left(x+5\right)}=\dfrac{-2}{x+5}\)
Để biểu thức trên nhận giá trị dương khi
\(x+5< 0\)do -2 < 0
\(\Leftrightarrow x< -5\)
Đúng 0
Bình luận (0)
Cho biểu thức với . a) Rút gọn biểu thức ; b) Tìm điều kiện của để ; c) Tìm các giá trị nguyên của để có giá trị nguyên; d)* Với , hãy tìm giá trị lớn nhất của . Bài 8: Cho biểu thức ; với . a) Tính giá trị biểu thức khi . b) Rút gọn biểu thức . c) So sánh với 1. d) Tìm để có giá trị nguyên.
Rút gọn biểu thức sau. Với giá trị nào của x, giá trị của biểu thức rút gọn là dương?
(\(\dfrac{\dfrac{x}{x+1}}{\dfrac{x^2}{x^2+x+1}}\) - \(\dfrac{2x+1}{x^2+x}\))\(\dfrac{x^2-1}{x-1}\)
\(\left(\dfrac{\dfrac{x}{x+1}}{\dfrac{x^2}{x^2+x+1}}-\dfrac{2x+1}{x^2+x}\right)\dfrac{x^2-1}{x-1}\)ĐK : \(x\ne\pm1\)
\(=\left(\dfrac{x}{x+1}.\dfrac{x^2+x+1}{x^2}-\dfrac{2x+1}{x\left(x+1\right)}\right)\left(x+1\right)=\left(\dfrac{x^2+x-1}{x^2+x}-\dfrac{2x+1}{x\left(x+1\right)}\right)\left(x+1\right)\)
\(=\left(\dfrac{x^2+x-1-2x-1}{x\left(x+1\right)}\right)\left(x+1\right)=\dfrac{x^2-3x-2}{x}\)
Đúng 0
Bình luận (0)
à xin lỗi mình nhầm dòng cuối
\(=\dfrac{x^2-x-2}{x}=\dfrac{\left(x+1\right)\left(x-2\right)}{x}\)
Để biểu thức trên nhận giá trị dương khi
\(\dfrac{\left(x+1\right)\left(x-2\right)}{x}>0\)bạn tự xét TH cả tử và mẫu nhé, mình đánh trên này bị lỗi
Đúng 0
Bình luận (0)
Cho biểu thức: a) Rút gọn P.b) Tìm giá trị nhỏ nhất của P.c) Tìm x để biểu thức Q nhận giá trị là số nguyên.
Đọc tiếp
Cho biểu thức:
a) Rút gọn P.
b) Tìm giá trị nhỏ nhất của P.
c) Tìm x để biểu thức Q= nhận giá trị là số nguyên.
a) Ta có: \(P=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\)
\(=\sqrt{x}\left(\sqrt{x}-1\right)-2\sqrt{x}-1+2\left(\sqrt{x}+1\right)\)
\(=x-\sqrt{x}-2\sqrt{x}-1+2\sqrt{x}+2\)
\(=x-\sqrt{x}+1\)
Đúng 2
Bình luận (0)
Rút gọn biểu thức:
A
a
2
+
2
a
2
a
+
10
+
a
−
5
a
+
50
−
5
a
2...
Đọc tiếp
Rút gọn biểu thức: A = a 2 + 2 a 2 a + 10 + a − 5 a + 50 − 5 a 2 a ( a + 5 ) .
a) Tìm điều kiện xác định của biểu thức A;
b) Rút gọn biểu thức;
c) Tính giá trị của biểu thức tại a = -1
d) Tìm giá trị của a để A = 0.
a) a ≠ 0 , a ≠ − 5
b) Ta có A = a 3 + 4 a 2 − 5 a 2 a ( a + 5 ) = a ( a − 1 ) ( a + 5 ) 2 a ( a + 5 ) = a − 1 2
c) Thay a = -1 (TMĐK) vào a ta được A = -1
d) Ta có A = 0 Û a = 1 (TMĐK)
Đúng 0
Bình luận (0)
Giá trị của biểu thức
2
y
2
x
4
4
y
2
;
y
0
khi rút gọn là? A. -x
y
2
B. x
y
2
C. -...
Đọc tiếp
Giá trị của biểu thức 2 y 2 x 4 4 y 2 ; y < 0 khi rút gọn là?
A. -x y 2
B. x y 2
C. - x 2 y
D. x 2 y
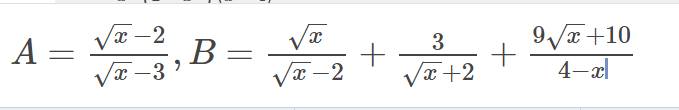
a,tính giá trị biểu thức A khi x=16/9
b,rút gọn biểu thức B
c,cho P=B/A,Tìm các giá trị của x là số thực đẻ P nhận giá trị nguyên
a: Khi x=16/9 thì \(A=\left(\dfrac{4}{3}-2\right):\left(\dfrac{4}{3}-3\right)=\dfrac{-2}{3}:\dfrac{-5}{3}=\dfrac{2}{5}\)
b: \(=\dfrac{x+2\sqrt{x}+3\sqrt{x}-6-9\sqrt{x}-10}{x-4}\)
\(=\dfrac{x-4\sqrt{x}-16}{x-4}\)
Đúng 1
Bình luận (0)
Bài 4: Cho biểu thức M (với x) a) Rút gọn M b) Tính giá trị của biểu thức M với x - 3Bài 5. Cho hai biểu thức: A và B a) Tính giá trị của biểu thức A khi x 5b) Rút gọn biểu thức Bc) Biết P A.B, tìm các số tự nhiên x để P ∈ Z
Đọc tiếp
Bài 4: Cho biểu thức M = ![]() (với x
(với x![]() )
)
a) Rút gọn M
b) Tính giá trị của biểu thức M với x = - 3
Bài 5. Cho hai biểu thức: A = ![]() và B =
và B = ![]()
a) Tính giá trị của biểu thức A khi x = 5
b) Rút gọn biểu thức B
c) Biết P = A.B, tìm các số tự nhiên x để P ∈ Z
Cho biểu thức Với 1) Rút gọn biểu thức 2) Tìm các giá trị của a để nhận giá trị nguyên.
Đọc tiếp
Cho biểu thức  Với
Với ![]()
1) Rút gọn biểu thức ![]()
2) Tìm các giá trị của a để ![]() nhận giá trị nguyên.
nhận giá trị nguyên.
Cho biểu thức: P 3/x+2 - 2/2-x -8/x^2-4a) Tìm điều kiện của biến x để giá trị của biểu thức P được xác định.b) Rút gọn biểu thức P.c) Tìm giá trị nguyên dương của x để giá trị của biểu thức P là một số nguyên dương.
Đọc tiếp
Cho biểu thức: P= 3/x+2 - 2/2-x -8/x^2-4
a) ![]() Tìm điều kiện của biến x để giá trị của biểu thức P được xác định.
Tìm điều kiện của biến x để giá trị của biểu thức P được xác định.
b) Rút gọn biểu thức P.
c) Tìm giá trị nguyên dương của x để giá trị của biểu thức P là một số nguyên dương.
a) ĐK:\(\begin{cases} x + 2≠0\\ x - 2≠0 \end{cases}\)⇔\(\begin{cases} x ≠ -2\\ x≠ 2 \end{cases}\)
Vậy biểu thức P xác định khi x≠ -2 và x≠ 2
b) P= \(\dfrac{3}{x+2}\)-\(\dfrac{2}{2-x}\)-\(\dfrac{8}{x^2-4}\)
P=\(\dfrac{3}{x+2}\)+\(\dfrac{2}{x-2}\)-\(\dfrac{8}{(x-2)(x+2)}\)
P= \(\dfrac{3(x-2)}{(x-2)(x+2)}\)+\(\dfrac{2(x+2)}{(x-2)(x+2)}\)-\(\dfrac{8}{(x-2)(x+2)}\)
P= \(\dfrac{3x-6+2x+4-8}{(x-2)(x+2)}\)
P=\(\dfrac{5x-10}{(x-2)(x+2)}\)
P=\(\dfrac{5(x-2)}{(x-2)(x+2)}\)
P=\(\dfrac{5}{x+2}\)
Vậy P=\(\dfrac{5}{x+2}\)
Đúng 1
Bình luận (0)
a: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
Đúng 0
Bình luận (0)
21 tháng 12 2021
a) ĐK:\(\left{\right. x + 2 \neq 0 \\ x - 2 \neq 0\)⇔\(\left{\right. x \neq - 2 \\ x \neq 2\)
Vậy biểu thức P xác định khi x≠ -2 và x≠ 2
b) P= \(\frac{3}{x + 2}\)-\(\frac{2}{2 - x}\)-\(\frac{8}{x^{2} - 4}\)
P=\(\frac{3}{x + 2}\)+\(\frac{2}{x - 2}\)-\(\frac{8}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)}\)
P= \(\frac{3 \left(\right. x - 2 \left.\right)}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)}\)+\(\frac{2 \left(\right. x + 2 \left.\right)}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)}\)-\(\frac{8}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)}\)
P= \( \frac{3 x - 6 + 2 x + 4 - 8}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)}\)
P=\(\frac{5 x - 10}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)}\)
P=\(\frac{5 \left(\right. x - 2 \left.\right)}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)}\)
P=\(\frac{5}{x + 2}\)
Vậy P=\(\frac{5}{x + 2}\)
Đúng 0
Bình luận (0)


















