giải phương trình: sin^4x+cos^4x/sin2x=1/2(tanx+cotX)
giải các pt
a) \(cosx+cos3x+\left(cos^4x-sin^4x\right).cos2x=0\)
b) \(cos^2\frac{x}{2}+sin^2x+cos2x=\frac{1}{2}\)
c) \(\left(tanx+cotx\right)^2+\frac{3}{sin2x}-7=0\)
a/
\(\Leftrightarrow2cos2x.cosx+\left(cos^2x+sin^2x\right)\left(cos^2x-sin^2x\right).cos2x=0\)
\(\Leftrightarrow2cos2x.cosx+cos^22x=0\)
\(\Leftrightarrow cos2x\left(2cosx+cos2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\left(1\right)\\2cosx+cos2x=0\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow2x=\frac{\pi}{2}+k\pi\Rightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\)
\(\left(2\right)\Leftrightarrow2cosx+2cos^2x-1=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=\frac{\sqrt{3}-1}{2}\\cosx=\frac{-\sqrt{3}-1}{2}< -1\left(l\right)\end{matrix}\right.\)
\(\Rightarrow x=\pm arccos\left(\frac{\sqrt{3}-1}{2}\right)+k2\pi\)
b/
\(\Leftrightarrow\frac{1}{2}+\frac{1}{2}cosx+1-cos^2x+2cos^2x-1=\frac{1}{2}\)
\(\Leftrightarrow cos^2x+\frac{1}{2}cosx=0\)
\(\Leftrightarrow cosx\left(cosx+\frac{1}{2}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=0\\cosx=-\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=\pm\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
c/ ĐKXĐ: ...
\(\Leftrightarrow\left(\frac{sinx}{cosx}+\frac{cosx}{sinx}\right)^2+\frac{3}{sin2x}-7=0\)
\(\Leftrightarrow\left(\frac{sin^2x+cos^2x}{sinx.cosx}\right)^2+\frac{3}{sin2x}-7=0\)
\(\Leftrightarrow\left(\frac{2}{sin2x}\right)^2+\frac{3}{sin2x}-7=0\)
Đặt \(\frac{1}{sin2x}=a\Rightarrow4a^2+3a-7=0\Rightarrow\left[{}\begin{matrix}a=1\\a=-\frac{7}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\frac{1}{sin2x}=1\\\frac{1}{sin2x}=-\frac{7}{4}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}sin2x=1\\sin2x=-\frac{4}{7}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}+k2\pi\\2x=arcsin\left(-\frac{4}{7}\right)+k2\pi\\2x=\pi-arcsin\left(-\frac{4}{7}\right)+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=\frac{1}{2}arcsin\left(-\frac{4}{7}\right)+k\pi\\x=\frac{\pi}{2}-\frac{1}{2}arcsin\left(-\frac{4}{7}\right)+k\pi\end{matrix}\right.\)
giải các pt
a) \(4sin^3x+3\sqrt{2}sin2x=8sinx\)
b) \(7cosx=4cos^3x+4sin2x\)
c) \(tanx+cotx=5-\frac{3}{sin^22x}\)
d) \(5\left(1+cosx\right)=2+sin^4x-cos^4x\)
e) \(2\left(cos^2x+cos^22x+cos^23x\right)=3\left(1+cosx.cos4x\right)\)
a/
\(\Leftrightarrow4sin^3x+6\sqrt{2}sinx.cosx-8sinx=0\)
\(\Leftrightarrow2sinx\left(2sin^2x+3\sqrt{2}cosx-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\Rightarrow x=k\pi\\2sin^2x+3\sqrt{2}cosx-4=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow2\left(1-cos^2x\right)+3\sqrt{2}cosx-4=0\)
\(\Leftrightarrow-2cos^2x+3\sqrt{2}cosx-2=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=\sqrt{2}>1\left(l\right)\\cosx=\frac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Rightarrow x=\pm\frac{\pi}{4}+k2\pi\)
b/
\(\Leftrightarrow4cos^3x+8sinx.cosx-7cosx=0\)
\(\Leftrightarrow cosx\left(4cos^2x+8sinx-7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=0\Rightarrow x=\frac{\pi}{2}+k\pi\\4cos^2x+8sinx-7=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow4\left(1-sin^2x\right)+8sinx-7=0\)
\(\Leftrightarrow-4sin^2x+8sinx-3=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=\frac{3}{2}\left(l\right)\\sinx=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
c/
ĐKXĐ; ...
\(\Leftrightarrow\frac{sinx}{cosx}+\frac{cosx}{sinx}-5+\frac{3}{sin^22x}=0\)
\(\Leftrightarrow\frac{sin^2x+cos^2x}{sinx.cosx}-5+\frac{3}{sin^22x}=0\)
\(\Leftrightarrow\frac{3}{sin^22x}+\frac{2}{sin2x}-5=0\)
Đặt \(\frac{1}{sin2x}=t\Rightarrow3t^2+2t-5=0\)
\(\Rightarrow\left[{}\begin{matrix}t=1\\t=-\frac{5}{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\frac{1}{sin2x}=1\\\frac{1}{sin2x}=-\frac{5}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}sin2x=1\\sin2x=-\frac{3}{5}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=\frac{1}{2}arcsin\left(-\frac{3}{5}\right)+k\pi\\x=\frac{\pi}{2}-\frac{1}{2}arcsin\left(-\frac{3}{5}\right)+k\pi\end{matrix}\right.\)
giải phương trình : \(\cos^4x-\sin^4x+\sqrt{3}\sin2x=1\)
Cm các đẳng thức sau không phụ thuộc vào giá trị x,y
\(\left(cotx+tanx\right)^2-\left(cotx-tanx\right)^2\)
\(cos^2x.cot^2x+3cos^2x-cot^2x+2sin^2x\)
\(sin^8x+cos^8x+6sin^4x.cos^4x+4sin^2x.cos^2x\left(sin^4x+cos^4x\right)+1\)
Mọi người giải chi tiết giúp mình, mình cảm ơn
\(A=cot^2x+tan^2x+2-\left(cot^2x+tan^2x-2\right)=4\)
\(B=cos^2x.cot^2x-cot^2x+cos^2x+2\left(sin^2x+cos^2x\right)\)
\(=cot^2x\left(cos^2x-1\right)+cos^2x+2\)
\(=-cot^2x.sin^2x+cos^2x+2\)
\(=-cos^2x+cos^2x+2=2\)
\(C=\left(sin^4x+cos^4x\right)^2+4sin^4x.cos^4x+4sin^2xcos^2x\left(sin^4x+cos^4x\right)+1\)
\(=\left(sin^4x+cos^4x+2sin^2x.cos^2x\right)^2+1\)
\(=\left(sin^2x+cos^2x\right)^4+1\)
\(=1^4+1=2\)
Chứng minh các biểu thức sau không phụ thuộc x:
a) A = \(2\left(sin^6x+cos^6x\right)-3\left(sin^4x+cos^4x\right)\)
b) \(B=\dfrac{1+cotx}{1-cotx}-\dfrac{2}{tanx-1}\)
c) C = \(2cos^4x-sin^4x+sin^2x.cos^2x+3sin^2x\)
Giả sử các biểu thức đều có nghĩa
\(A=2\left(\left(sin^2x\right)^3+\left(cos^2x\right)^3\right)-3\left(sin^4x+cos^4x+2sin^2xcos^2x-2sin^2xcos^2x\right)\)
\(A=2\left(sin^2x+cos^2x\right)\left(\left(sin^2x+cos^2x\right)^2-3sin^2xcos^2x\right)-3\left(\left(sin^2x+cos^2x\right)^2-2sin^2xcos^2x\right)\)
\(A=2\left(1-3sin^2xcos^2x\right)-3\left(1-2sin^2xcos^2x\right)\)
\(A=2-6sin^2xcos^2x-3+6sin^2xcos^2x=-1\)
b/ \(B=\dfrac{1+cotx}{1-cotx}-\dfrac{2}{tanx-1}=\dfrac{1+cotx}{1-cotx}-\dfrac{2}{\dfrac{1}{cotx}-1}\)
\(B=\dfrac{1+cotx}{1-cotx}-\dfrac{2cotx}{1-cotx}=\dfrac{1+cotx-2cotx}{1-cotx}=\dfrac{1-cotx}{1-cotx}=1\)
c/ \(C=cos^4x-sin^4x+cos^4x+sin^2xcos^2x+3sin^2x\)
\(C=\left(cos^2x-sin^2x\right)\left(cos^2x+sin^2x\right)+cos^2x\left(cos^2x+sin^2x\right)+3sin^2x\)
\(C=cos^2x-sin^2x+cos^2x+3sin^2x\)
\(C=2cos^2x+2sin^2x=2\left(cos^2x+sin^2x\right)=2\)
Giải phương trình cotx - tanx + 4sin2x = 2/sin2x
Đối với những phương trình lượng giác chứa tanx, cotx, sin2x hoặc cos2x, ta có thể đưa về phương trình chứa cosx, sinx, sin2x, hoặc cos2x ngoài ra cũng có thể đặt ẩn phụ t = tanx để đưa về một phương trình theo t.
Cách 1: Điều kiện của phương trình:
sin2x ≠ 0 ⇔ cos2x ≠ 1 hoặc cos2x ≠ -1 (1)
Ta có:
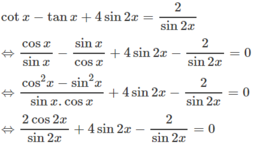
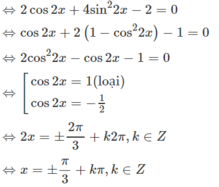
Cách 2. Đặt t = tanx
Điều kiện t ≠ 0
Phương trình đã cho có dạng
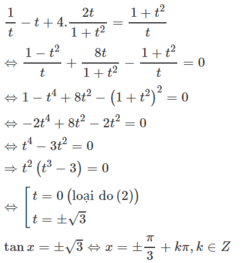
Giải các phương trình :
1) \(\frac{\sin^4x+\cos^4x}{\sin2x}=\frac{1}{2}\left(\tan x+\cot2x\right)\)
2) \(\frac{1}{\sin x}+\frac{1}{\sin\left(x-\frac{3\pi}{2}\right)}=4\sin\left(\frac{7\pi}{4}-x\right)\)
3)\(2\left(\cos^42x-\sin^42x\right)+\cos8x-\cos4x=0\)
4)\(\frac{\sin^4x+\cos^4x}{5\sin2x}=\frac{1}{2}\cot2x-\frac{1}{8\sin2x}\)
5)\(\sin^4x+\cos^4x-3\sin2x+\frac{5}{2}\sin^22x=0\)
Giải phương trình c o t x - 1 = cos 2 x 1 + tan x + sin 2 x - 1 2 sin 2 x
Điều kiện của phương trình: sinx ≠ 0, cos ≠ 0, tan ≠ -1.
Biến đổi tương đương đã cho, ta được
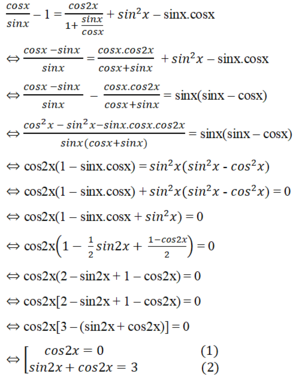
Phương trình (2) vô nghiệm vì |sin2x + cos2x| ≥ √2.
Phương trình (1) có nghiệm 2x = π/2+kπ,k ∈ Z
⇒ x = π/4+ k π/2,k ∈ Z.
Giá trị x = π/4+ k π/2, k = 2n + 1,
với n ∈ Z bị loại do điều kiện tanx ≠ -1.
Cm biểu thức ko phụ thuộc x
B=\(\dfrac{sin^4x-cos^4x+cos^2x}{2\left(1-cosx\right)\left(1+cosx\right)}\)
Cm
\(\dfrac{1+sin2x-cos2x}{1+sin2x+cos1x}=tanx\)
a) \(B=\dfrac{sin^4x-cos^4x+cos^2x}{2\left(1-cosx\right)\left(1+cosx\right)}\)
\(B=\dfrac{\left(sin^2x\right)^2-\left(cos^2x\right)^2+cos^2x}{2\left(1-cos^2x\right)}\)
\(B=\dfrac{\left(sin^2x-cos^2x\right)\left(sin^2x+cos^2x\right)+cos^2x}{2\left(sin^2x+cos^2x-cos^2x\right)}\)
\(B=\dfrac{sin^2x-cos^2x+cos^2x}{2sin^2x}=\dfrac{sin^2x}{2sin^2x}=\dfrac{1}{2}\)
b) \(\dfrac{1+sin2x-cos2x}{1+sin2x+cos2x}=tanx\)
\(VT=\dfrac{1+2sinx.cosx-\left(1-2sin^2x\right)}{1+2sinx.cosx+2cos^2x-1}\)
\(VT=\dfrac{1+2sinx.cosx-1+2sin^2x}{2sinx.cosx+2cos^2x}\)
\(VT=\dfrac{2sinx.cosx+2sin^2x}{2sinx.cosx+2cos^2x}\)
\(VT=\dfrac{2sinx\left(cosx+sinx\right)}{2cosx\left(sinx+cosx\right)}=\dfrac{sinx}{cosx}=tanx=VP\) ( đpcm )
p/s : sửa \(cos1x\rightarrow cos2x\)