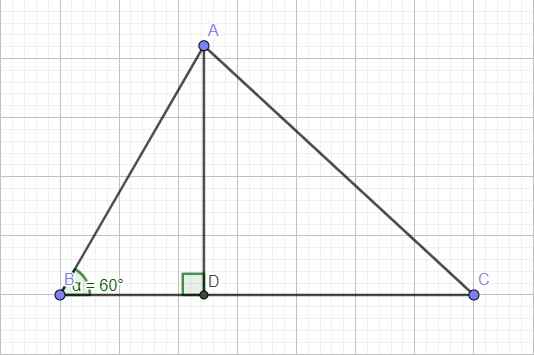
cho ΔABC có góc B=60o, AC=13, BC lớn hơn AB là 7cm. tính AB, BC

Những câu hỏi liên quan
cho ΔABC có góc B bằng 60o, BC=8cm, AB+AC=12cm. Tính AB,AC
Kẻ đường cao AD, đặt \(AB=x>0\) ; \(BD=y>0\)
\(\Rightarrow AC=12-x\) ; \(CD=8-y\)
Trong tam giác vuông ABD:
\(BD=AB.cosB\Leftrightarrow y=x.cos60^0=\dfrac{x}{2}\) \(\Rightarrow CD=8-\dfrac{x}{2}\)
Theo định lý Pitago:
\(\left\{{}\begin{matrix}AD^2=AB^2-BD^2\\AD^2=AC^2-CD^2\end{matrix}\right.\) \(\Rightarrow AB^2-BD^2=AC^2-CD^2\)
\(\Leftrightarrow x^2-\left(\dfrac{x}{2}\right)^2=\left(12-x\right)^2-\left(8-\dfrac{x}{2}\right)^2\)
\(\Leftrightarrow16x-80=0\)
\(\Rightarrow x=5\)
Vậy \(\left\{{}\begin{matrix}AB=5\\AC=7\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Cho ΔABC vuông tại A có AB > AC, M là điểm tuỳ ý trên BC. Qua M kẻ Mx vuông góc với BC và cắt AB tại I cắt CA tại D.
a. Chứng minh ΔABC đồng dạng với ΔMDC
b. Chứng minh: BI.BA = BM.BC
c. Cho góc ACB = 60o và SΔCDB = 60 cm². Tính SΔCMA.
a: Xét ΔCMD vuông tại M và ΔCAB vuông tại A có
góc C chung
=>ΔCMD đồng dạng với ΔCAB
b: Xét ΔBMI vuông tại M và ΔBAC vuông tại A có
góc MBI chung
=>ΔBMI đồng dạng với ΔBAC
=>BM/BA=BI/BC
=>BM*BC=BA*BI
c: ΔCMD đồng dạng với ΔCAB
=>CM/CA=CD/CB
=>CM/CD=CA/CB
=>ΔCMA đồng dạng với ΔCDB
=>S CMA/S CDB=(CA/CB)^2=1/4
=>S CMA=15cm2
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc B=60 độ, AC=13 cm , BC-AB=7cm. Tính AB,BC
Bài 1: ABC có AB = 5cm, AC = 10cm, BC = 7cm. Biết ABC đồng dạng với DEF có cạnh lớn nhất dài 15cm. Hãy tính các cạnh còn lại của DEF.
Bài 2: Cho ΔMNP ∽ ΔABC. Biết MN=4cm, NP=6cm, AB=2cm, 𝑃̂=40o . Tính BC, 𝐶̂.
Cho ΔABC có AB=2; BC=3;AC=6 a) Tính diện tích ΔABC=? b) Tính độ dài đường trung tuyến kẻ từ C c) Tính bán kính đường tròn ngoại tiếp ΔABC d) Tính số đo góc lớn nhất trong ΔABC.
AB+BC<AC
nên ko có tam giác ABC thỏa mãn nha bạn
Đúng 2
Bình luận (0)
ΔABC có AB=5cm, AC=8cm, BC=7cm tìm số đo các góc của Δ ABC toán 9
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2.AB.AC}=\dfrac{5^2+8^2-7^2}{2.5.8}=\dfrac{1}{2}\\ \Rightarrow\widehat{A}=60^o\\ cosB=\dfrac{AB^2+BC^2-AC^2}{2.AB.BC}=\dfrac{5^2+7^2-8^2}{2.5.7}=\dfrac{1}{7}\\ \Rightarrow\widehat{B}=81^o47'\\ cosC=\dfrac{AC^2+BC^2-AB^2}{2.AC.BC}=\dfrac{8^2+7^2-5^2}{2.8.7}=\dfrac{11}{14}\\ \Rightarrow\widehat{C}=38^o13'\)
Đúng 1
Bình luận (0)
\(cosA=\dfrac{5^2+8^2-7^2}{2\cdot5\cdot8}=\dfrac{1}{2}\)
=>góc A=60 độ
AB/sinC=AC/sinB=BC/sinA
=>5/sinC=8/sinB=7/sin60
=>góc C=38 độ; góc B=82 độ
Đúng 0
Bình luận (0)
Cho ΔABC, góc C= 90o, góc A=60o. Tia phân giác của góc BAC cắt BC tại E. Kẻ EK⊥AB ( K ∈ AB ). Kẻ BD⊥AE ( D ∈ AE ). Chứng minh rằng
a. AC=AK
b. EB>AC
c. CK // BD
a) Xét ΔACE vuông tại C và ΔAKE vuông tại K có
AE chung
\(\widehat{CAE}=\widehat{KAE}\)(AE là tia phân giác của \(\widehat{CAK}\))
Do đó: ΔACE=ΔAKE(Cạnh huyền-góc nhọn)
Suy ra: AC=AK(Hai cạnh tương ứng)
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác BC có góc B gằng 60 độ, AC=13cm, BC-AB=7cm. Tính AB, BC
1.
a) Cho ΔABC có : AC=5cm, BC=3cm. Tìm cạnh AB biết, AB là số nguyên và AB>6cm
b) Cho ΔABC có: AB=8cm, AC=6cm. Tính BC, biết BC là số nguyên BC<4cm
a: AC-BC<AB<AC+BC
=>5<AB<8
mà AB>6
nên AB=7cm
b: AB-AC<BC<AB+AC
=>2<BC<14
mà BC<4
nên BC=3cm
Đúng 1
Bình luận (0)