Cho hình thang ABCD có AD // BC và AD=2BC ,B(4;0) phương trình đường chéo AC là 2x-y-3=0 trung điểm E của AD thuộc đường thẳng d:x-2y+10=0.Tìm tọa độ các đỉnh còn lại của hình thang biết cot ADC bằng 2

Những câu hỏi liên quan
cho hình chóp s abcd có đáy abcd là hình bình thang AD//BC và AD bằng 2BC gọi E,F lần lượt là trung điểm SA và CD chứng minh CI//(BEF)
Cho hình chóp s.abcd có đáy abcd là hình thang, ad // bc, ad=2bc. Gọi O là giao điểm của ac và bd, e là điểm trên cạnh ad sao cho ed = 2ea và N là điểm trên cạnh sd sao cho nd =2ns
a) c/m bc // (sad)
b) c/m (oen) // (sab)
Xem chi tiết
Bài làm:
a) Do BC//AD và AD\(\subset\) (SAD)
=> BC// (SAD)
b) có \(\dfrac{DE}{AE}=\dfrac{DN}{NS}=2\)
=> NE//SA
do BC//AD => \(\dfrac{BC}{AD}=\dfrac{OB}{OD}=\dfrac{1}{2}\) => \(\dfrac{DE}{AE}=\dfrac{OD}{OB}=2\) => OE//AB
Do NE//SA và OE//AB mà OE,NE \(\subset\)(ONE); SA,SB\(\subset\) (SAB)
=> (ONE) //(SAB)
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang,
A
B
/
/
B
C
,
A
D
2
B
C
.
Vẽ
S
S
song song và bằng BC ta được hình đa diện mới
S
S
A
B
C
D
. Khi đó
V
S
S
A...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang, A B / / B C , A D = 2 B C . Vẽ S S ' song song và bằng BC ta được hình đa diện mới S S ' A B C D . Khi đó V S S ' A B C D V S . A B C D bằng
A. 5/3
B. 3/2
C. 4/3
D. 3
Đáp án C
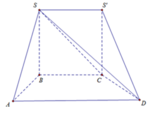
Ta có V D . S S ' C = V D . S C B = V S . B C D
Mặt khác S B C D = 1 2 S A B D = 1 3 S A B C D
Do đó V D . S S ' C = V D . S C B = V S . B C D = 1 3 V S . A B C D
Khi đó V S S ' A B C D V S . A B C D = 1 3 + 1 1 = 4 3
Đúng 0
Bình luận (0)
Cho ABCD là hình thang vuông tại A,B (AD là đáy lớn). AD = 2BC và AB = BC = a
a. Tính vecto CD - vecto CB
b. Gọi I trung điểm AD. CM: vecto BI + vecto BC - vecto BA = vecto AD
Cho khối chóp S.ABCD có thể tích
V
6
a
3
đáy ABCD là hình thang với hai đáy AD và BC thỏa mãn AD2BC diện tích tam giác SCD bằng
34
a
2
( thao khảo hình vẽ). Khoảng cách từ đỉnh B đến mặt phẳng (SCD) bằng A.
3
34
34
a
B. ...
Đọc tiếp
Cho khối chóp S.ABCD có thể tích V = 6 a 3 đáy ABCD là hình thang với hai đáy AD và BC thỏa mãn AD=2BC diện tích tam giác SCD bằng 34 a 2 ( thao khảo hình vẽ). Khoảng cách từ đỉnh B đến mặt phẳng (SCD) bằng
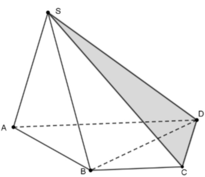
A. 3 34 34 a
B. 3 34 17 a
C. 34 17 a
D. 9 34 34 a
Theo công thức tính thể tích chóp có
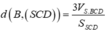
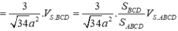
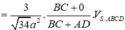
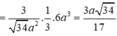
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình thang ABCD với AD//BC và AD = 2BC. Gọi M là điểm trên cạnh SD thỏa mãn SM = 1/3SD. Mặt phẳng (ABM) cắt cạnh SC tại N. Tính SN/ SC
Vẫn dùng kĩ thuật cũ:
\(\overrightarrow{AD}-2\overrightarrow{BC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AS}+\overrightarrow{SD}-2\overrightarrow{BS}-2\overrightarrow{SC}=0\)
\(\Leftrightarrow\overrightarrow{SA}=2\overrightarrow{SB}-2\overrightarrow{SC}+\overrightarrow{SD}\) (1)
Đặt \(\overrightarrow{SC}=x.\overrightarrow{SN}\)
Giả thiết suy ra \(\overrightarrow{SD}=3\overrightarrow{SM}\)
Thế vào (1): \(\overrightarrow{SA}=2\overrightarrow{SB}-2x.\overrightarrow{SN}+3\overrightarrow{SM}\)
Do A, B, N, M đồng phẳng
\(\Rightarrow2-2x+3=1\)
\(\Rightarrow x=2\Rightarrow SC=2SN\Rightarrow SN=\dfrac{1}{2}SC\)
Đúng 2
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B,
A
D
2
B
C
,
S
A
⊥
A
B
C
D
.
Gọi E, M lần lượt là trung điểm của AD và SD. K là hình chiếu của E trên SD. Góc giữa (SCD) và (SAD) là: A. góc AMC B. góc EKC C. góc AKC D. góc CSA
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, A D = 2 B C , S A ⊥ A B C D . Gọi E, M lần lượt là trung điểm của AD và SD. K là hình chiếu của E trên SD. Góc giữa (SCD) và (SAD) là:
A. góc AMC
B. góc EKC
C. góc AKC
D. góc CSA
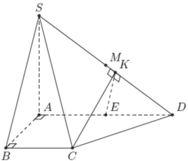
Ta có A E = B C A E / / B C suy ra AECB là hình bình hành. Do A B C ^ = 90 0 nên AECB là hình chữ nhật.
Suy ra C E ⊥ A D mà S A ⊥ C E ⇒ C E ⊥ S A D ⇒ C E ⊥ S D .
Ta lại có E K ⊥ S D ⇒ S D ⊥ E K M ⇒ S D ⊥ C K .
Suy ra góc giữa hai mặt phẳng (SAD) và (SCD) là góc EKC
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AD || BC, AD= 2BC ). Gọi M, N lần lượt là trung điểm SA và AB.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
b) Chứng minh MN//(SBC)
c) Gọi O là giao điểm của AC và BD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (OMN)
a: Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
b: Xét ΔSAB có
M,N lần lượt là trung điểm của AS,AB
=>MN là đường trung bình của ΔSAB
=>MN//SB
Ta có: MN//SB
SB\(\subset\)(SBC)
MN ko nằm trong mp(SBC)
Do đó: MN//(SBC)
Đúng 0
Bình luận (0)
Cho hình thang ABCD có AB90o, AD2AB2BC2a. Tính thể tích khối tròn xoay sinh ra khi quay hình thang ABCD xung quanh trục CD A.
7
2
πa
3
6
B.
7
πa
3
12
C.
7
2...
Đọc tiếp
Cho hình thang ABCD có A=B=90o, AD=2AB=2BC=2a. Tính thể tích khối tròn xoay sinh ra khi quay hình thang ABCD xung quanh trục CD

A. 7 2 πa 3 6
B. 7 πa 3 12
C. 7 2 πa 3 12
D. 7 πa 3 6
Chọn đáp án A.
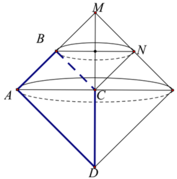
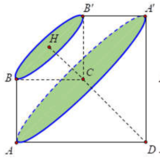
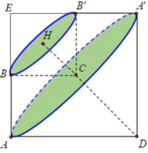
Gọi M là giao điểm của AB và CD. Từ B kẻ đường thẳng song song với AC, cắt CM tại N.
Khi quay ABCD quanh trục CD ta được hai phần:
+ Tam giác ACD sinh ra khối nón với bán kính đáy
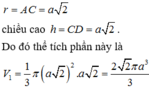

Đúng 0
Bình luận (0)















