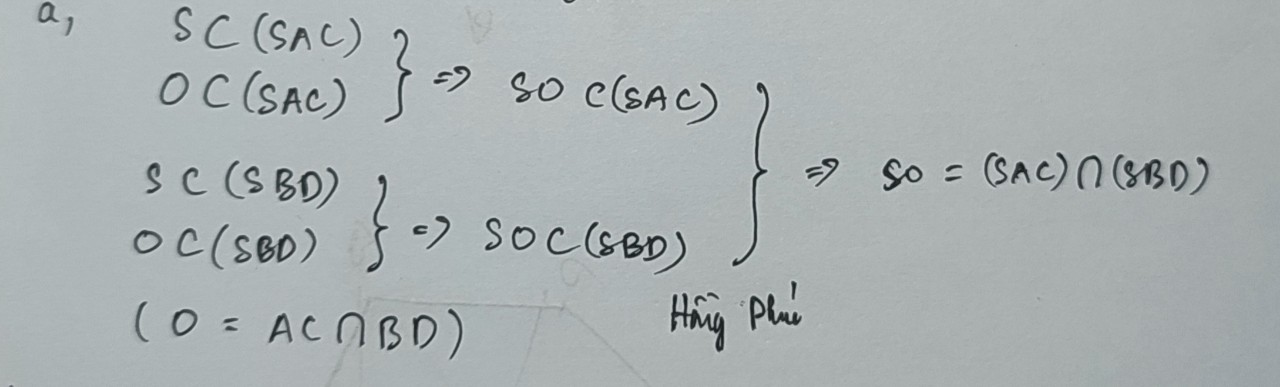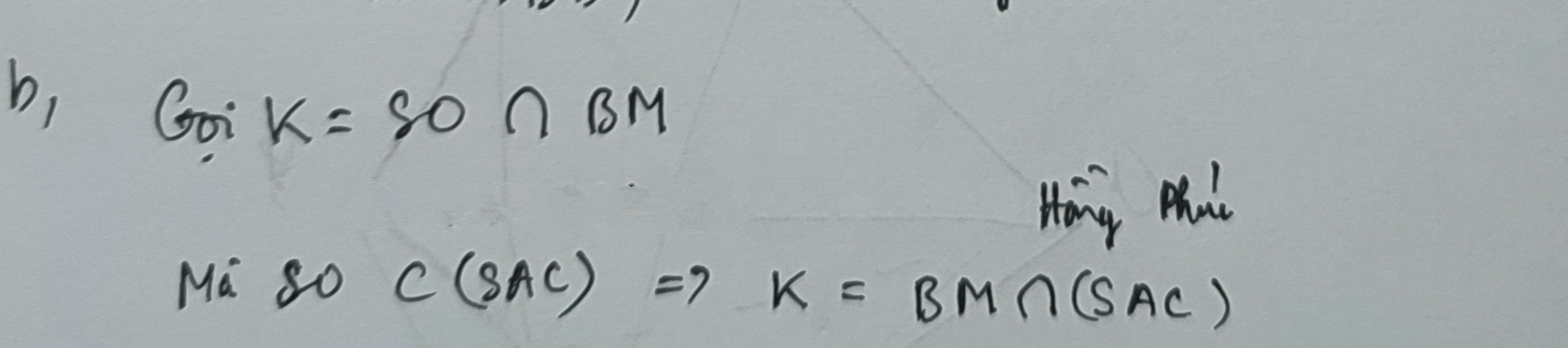Cho chóp S.ABCD. M là trung điểm của SD. Tìm giao điểm của (ABM) và SC

Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm SC. Tìm giao điểm của đường thẳng SD và (ABM)
Cho hình chóp tứ giác S.ABCD có AB và CD không song song. Gọi M là trung điểm của SD a) tìm giao tuyến của 2 mp(SAC) và (SBD) b)tìm giao điểm của BM với (SAC) c) tìm giao điểm của(ABM) với SC
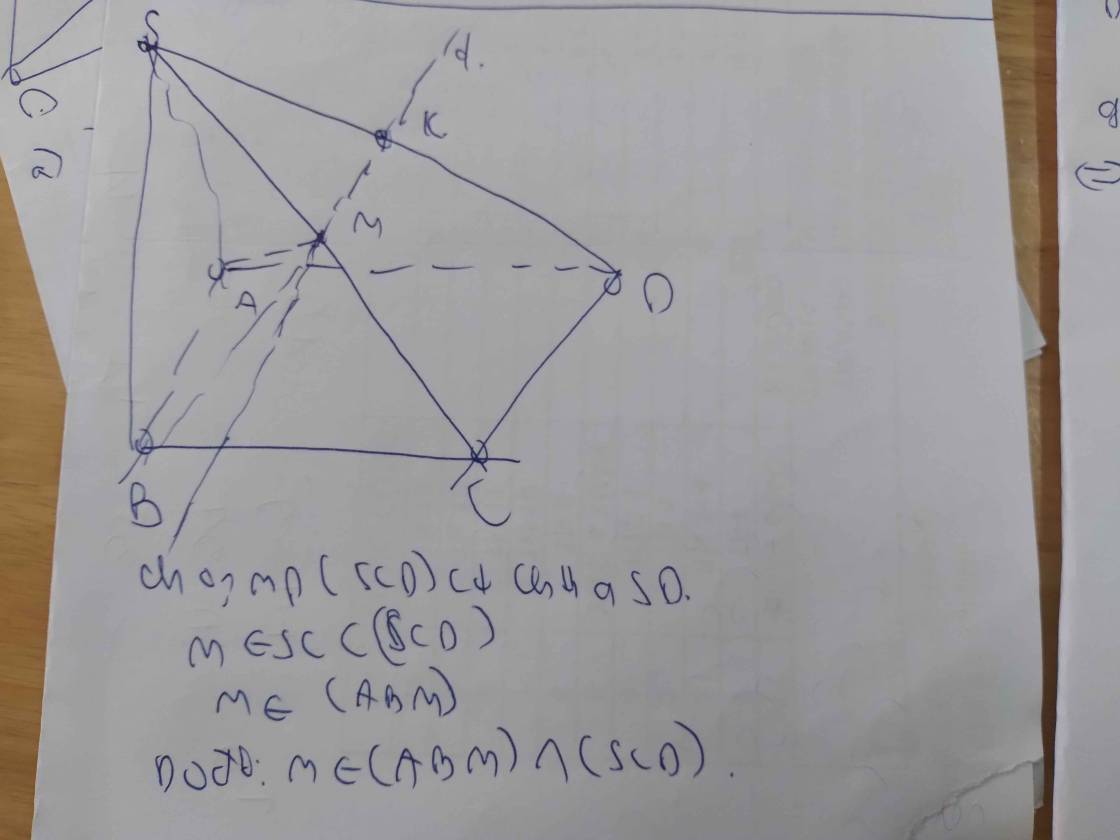
Cho hình chóp S.ABCD có đáy là hình thang ABCD, đáy lớn AB, M là trung điểm của SD.
a. Tìm giao tuyến của (ABM) và (SCD).
b. Gọi N là trung điểm của SC, P là một điểm trên cạnh BC và khác với điểm B và điểm C. Tìm giao điểm Q của SD với (ANP).
Cho chóp S.ABCD. M, N lần lượt là trung điểm của SB, SD. Tìm giao điểm của (AMN) và SC.
MN là đường trung bình tam giác SBD \(\Rightarrow MN||BD\)
\(\Rightarrow\) Giao tuyến của (AMN) và (ABCD) là 1 đường thẳng song song BD
Trong mp (ABCD), qua A kẻ đường thẳng d song song BD cắt CD kéo dài tại E
Trong mp (SCD), nối EN kéo dài cắt SC tại F
\(\Rightarrow F=SC\cap\left(AMN\right)\)
Đúng 3
Bình luận (2)
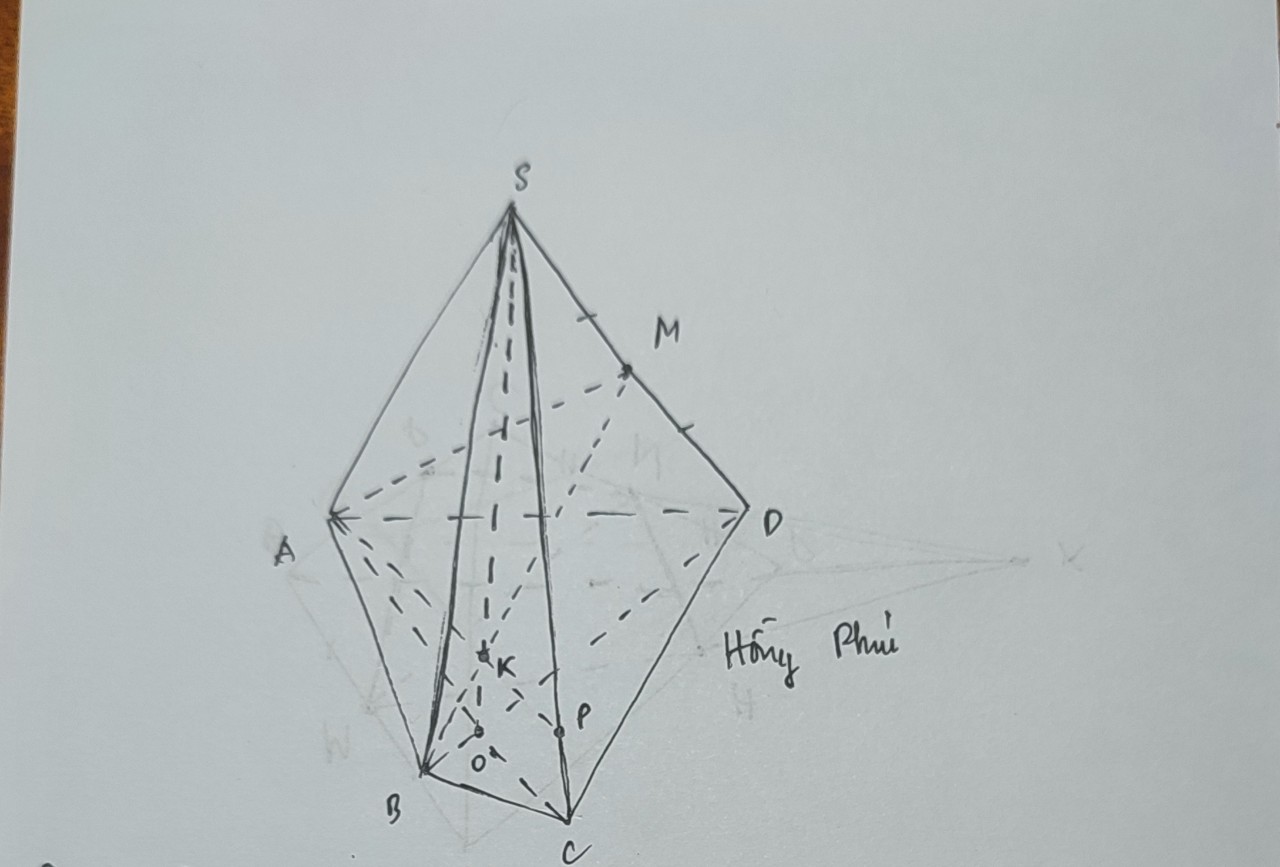
Cho hình Chóp S.ABCD có đáy là hình thang, đáy lớn AB. Gọi O là giao điểm của AC và BD
a. Tìm giao tuyến của hai mặt phẳng (SAD) và (SAB), (SAB)và (SCD)
b. Trên SC lấy điểm M tùy ý. Tìm giao điểm K của SD và mp (ABM)
c. Tìm thiết diện của hình chóp với mặt phẳng (ABM)
giúp mình với
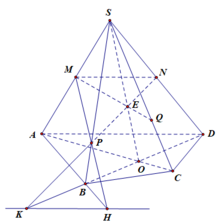
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi O là giao điểm của AC và BD; M,N lần lượt là trung điểm của SB,SD; P thuộc đoạn SC và không là trung điểm của SC.a) Tìm giao điểm E của đường thẳng SO và mặt phẳng left( {MNP} right).b) Tìm giao điểm Q của đường thẳng SA và mặt phẳng left( {MNP} right).c) Gọi I,J,K lần lượt là giao điểm của QM và AB, QP và AC, QN và A{rm{D}}. Chứng minh I,J,K thẳng hàng.
Đọc tiếp
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(O\) là giao điểm của \(AC\) và \(BD\); \(M,N\) lần lượt là trung điểm của \(SB,SD\); \(P\) thuộc đoạn \(SC\) và không là trung điểm của \(SC\).
a) Tìm giao điểm \(E\) của đường thẳng \(SO\) và mặt phẳng \(\left( {MNP} \right)\).
b) Tìm giao điểm \(Q\) của đường thẳng \(SA\) và mặt phẳng \(\left( {MNP} \right)\).
c) Gọi \(I,J,K\) lần lượt là giao điểm của \(QM\) và \(AB\), \(QP\) và \(AC\), \(QN\) và \(A{\rm{D}}\). Chứng minh \(I,J,K\) thẳng hàng.
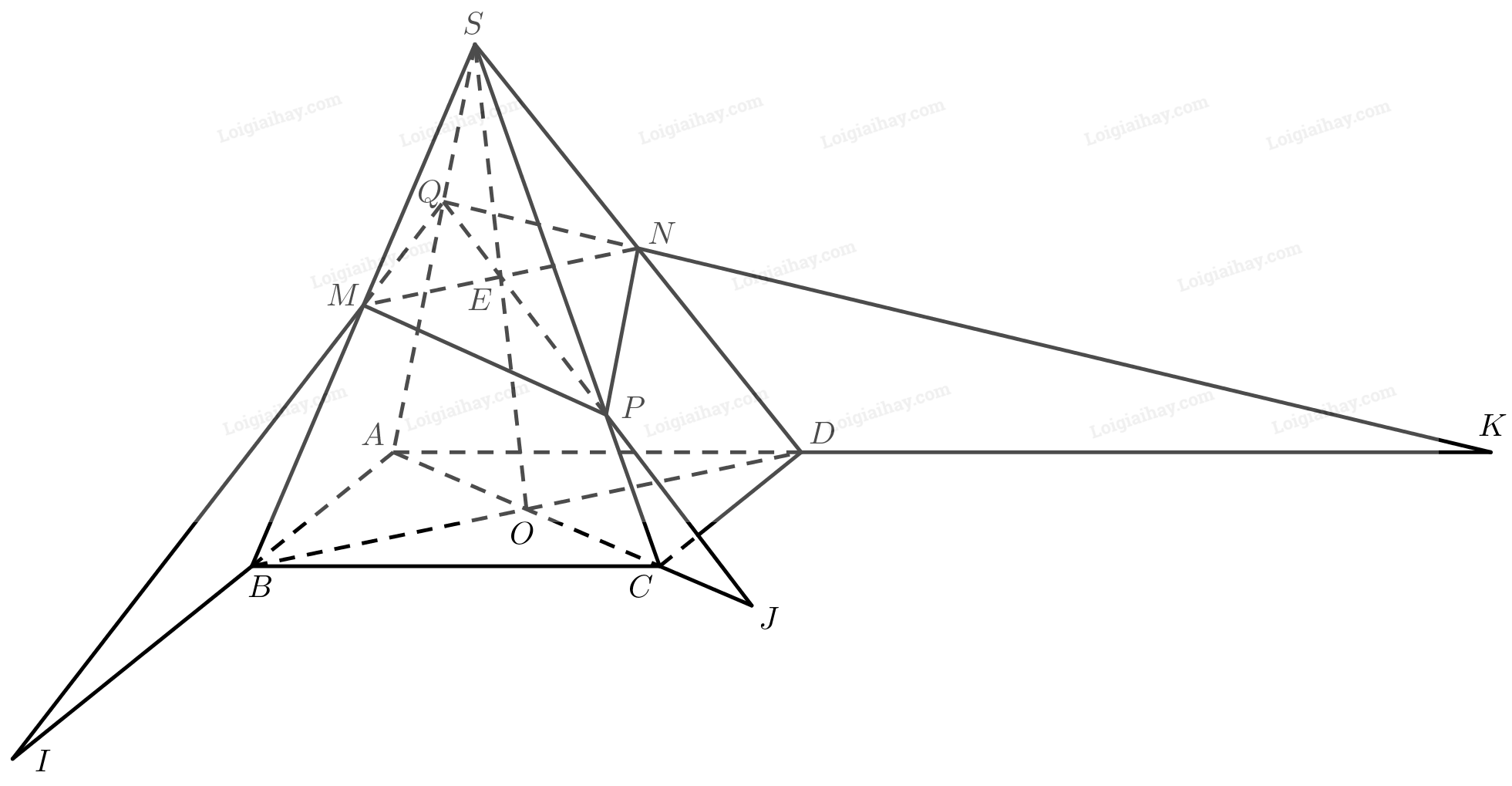
a) Gọi \(E\) là giao điểm của \(SO\) và \(MN\). Ta có:
\(\left. \begin{array}{l}E \in MN \subset \left( {MNP} \right)\\E \in S{\rm{O}}\end{array} \right\} \Rightarrow E = S{\rm{O}} \cap \left( {MNP} \right)\)
b) Gọi \(Q\) là giao điểm của \(SA\) và \(EP\). Ta có:
\(\left. \begin{array}{l}Q \in EP \subset \left( {MNP} \right)\\Q \in S{\rm{A}}\end{array} \right\} \Rightarrow Q = S{\rm{A}} \cap \left( {MNP} \right)\)
c) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in QM \subset \left( {MNP} \right)\\I \in AB \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow I \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}J \in QP \subset \left( {MNP} \right)\\J \in AC \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow J \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}K \in QN \subset \left( {MNP} \right)\\K \in AD \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow K \in \left( {MNP} \right) \cap \left( {ABCD} \right)\end{array}\)
Do đó, \(I,J,K\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {ABCD} \right)\).
Vậy \(I,J,K\) thẳng hàng.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD. Gọi M,N lần lượt là trung điểm của cạnh SA,SD. P là điểm thuốc cạnh SB sao cho SP=3PB. a, Tìm giao điểm Q của SC và (MNP) b, Tìm giao tuyến của (MNP) và (ABCD)
Cho hình chóp S.ABCD đáy là hình bình hành tâm O. Gọi M,N là trung điểm SB,SC; lấy điểm P thuộc SA.
a. Tìm giao tuyến của (SAB) và (SCD)
b. Tìm giao điểm SD và (MNP)
c. Tìm thiết diện hình chóp và (MNP). Thiết diện là hình gì?
Cho hình chóp S.ABCD. Gọi M, N lần lượt là trung điểm của cạnh SA, SD, P là điểm thuộc cạnh SB sao cho: SP 3 PB. Gọi O là giao điểm của AC và BD; E là giao điểm của PN và SO. Tìm giao điểm Q của SC và (MNP). A. Q là giao điểm của ME và SA B. Q là giao điểm của MO và SC C. Q là giao điểm của SC và PE D. Q là giao điểm của ME và SC
Đọc tiếp
Cho hình chóp S.ABCD. Gọi M, N lần lượt là trung điểm của cạnh SA, SD, P là điểm thuộc cạnh SB sao cho: SP = 3 PB. Gọi O là giao điểm của AC và BD; E là giao điểm của PN và SO. Tìm giao điểm Q của SC và (MNP).
A. Q là giao điểm của ME và SA
B. Q là giao điểm của MO và SC
C. Q là giao điểm của SC và PE
D. Q là giao điểm của ME và SC