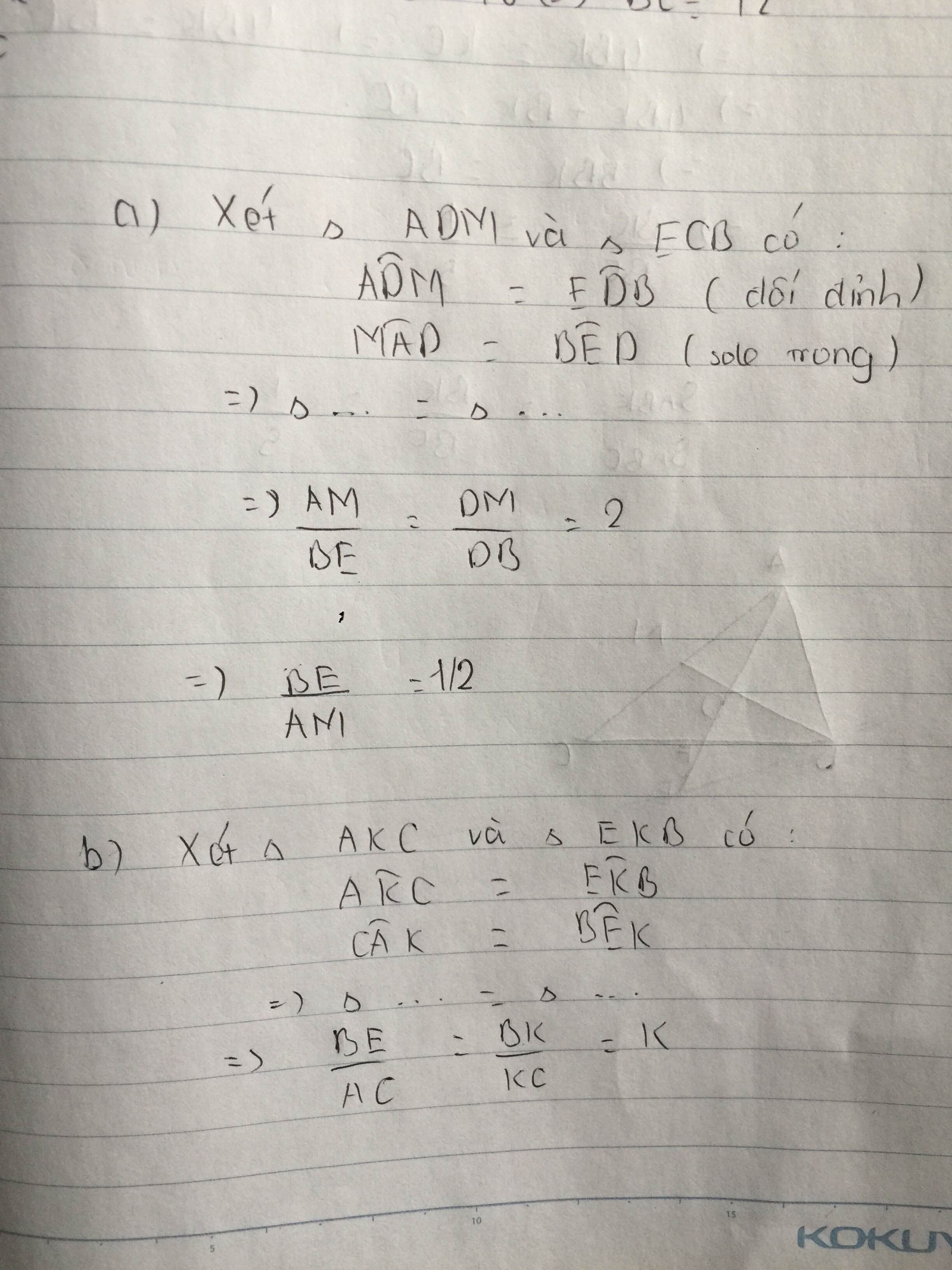Cho ΔABC, điểm M(-1/2 ; 3/2) là trung điểm AB. H(-2;4) là chân đường cao BH, I(-1;1) là tâm đường tròn ngoại tiếp ΔABC. Tìm tọa độ điểm C?

Những câu hỏi liên quan
Bài 1:Cho ΔABC có BC2AB.Gọi M là trung điểm của BC, N là trung điểm của BM.Tia đối tia NA lấy điểm E sao cho ANEN.a, CM: ΔNABΔNEM.b, CM:ΔMAB cân.c, CM:M là trọng tâm của ΔAEC.d, CM: AB2/3 AN.Bài 2: cho ΔABC vuông tại C, lấy D∈AB sao cho ADAB. Kẻ qua D đường thẳng vuông góc với AB cắt BC tại E, AE cát CD tại I.a, CM: AE là phân giác của góc CAB.b, CM: AD là đường trung trực của CD.c, So sánh CD và BCd, M là trung điểm của BC, DM cắt BI tại G. CG cắt DB tại K. CM:K là trung điểm của DB.giúp mình v...
Đọc tiếp
Bài 1:Cho ΔABC có BC=2AB.Gọi M là trung điểm của BC, N là trung điểm của BM.Tia đối tia NA lấy điểm E sao cho AN=EN.
a, CM: ΔNAB=ΔNEM.
b, CM:ΔMAB cân.
c, CM:M là trọng tâm của ΔAEC.
d, CM: AB>2/3 AN.
Bài 2: cho ΔABC vuông tại C, lấy D∈AB sao cho AD=AB. Kẻ qua D đường thẳng vuông góc với AB cắt BC tại E, AE cát CD tại I.
a, CM: AE là phân giác của góc CAB.
b, CM: AD là đường trung trực của CD.
c, So sánh CD và BC
d, M là trung điểm của BC, DM cắt BI tại G. CG cắt DB tại K. CM:K là trung điểm của DB.
giúp mình với❗❗❗❗❗❗
2: Sửa đề: AD=AC
a: Xét ΔACE vuông tại C và ΔADE vuông tại D có
AE chung
AC=AD
=>ΔACE=ΔADE
=>góc CAE=góc DAE
=>AE là phân giác của góc CAD
b: AC=AD
EC=ED
=>AE là trung trực của CD
1:
a: Xét ΔNAB và ΔNEM có
NA=NE
góc ANB=góc ENM
NB=NM
=>ΔNAB=ΔNEM
b: Xét ΔBAM có BA=BM
nên ΔBAM cân tại B
c: Xét ΔCAE có
CN là trung tuyến
CM=2/3CN
=>M là trọng tâm
Đúng 0
Bình luận (0)
Bài 1: Cho ΔABC; I là trung điểm BC. Trên AB lấy M; N sao choAM MN NB. Đường thẳng CM cắt AI tại K. CMR: KA KMBài 2: Cho ΔABC vuông tại A có AB 12 cm, BC 13cm. Gọi M, N lần lượtlà trung điểm của AB và BC.a. Chứng minh: MN vuông góc ABb. Tính MN?Bài 3: Cho ΔABC có AB 16cm, BC 20cm, AC 12cma. CM: ΔABC vuông tại Ab. Gọi M là trung điểm của BC. Kẻ MF vuông góc AC tại F. CM: FA FCc. Gọi E là trung điểm của AB. CM: ME vuông góc với AB và tính độ dàiME.
Đọc tiếp
Bài 1: Cho ΔABC; I là trung điểm BC. Trên AB lấy M; N sao cho
AM = MN = NB. Đường thẳng CM cắt AI tại K. CMR: KA = KM
Bài 2: Cho ΔABC vuông tại A có AB = 12 cm, BC = 13cm. Gọi M, N lần lượt
là trung điểm của AB và BC.
a. Chứng minh: MN vuông góc AB
b. Tính MN?
Bài 3: Cho ΔABC có AB = 16cm, BC = 20cm, AC = 12cm
a. CM: ΔABC vuông tại A
b. Gọi M là trung điểm của BC. Kẻ MF vuông góc AC tại F. CM: FA = FC
c. Gọi E là trung điểm của AB. CM: ME vuông góc với AB và tính độ dài
ME.
Bài 1:
Xét ΔBMC có
N là trung điểm của BM
I là trung điểm của BC
Do đó: NI là đường trung bình của ΔBMC
Suy ra: NI//MK
Xét ΔANI có
M là trung điểm của AN
MK//NI
Do đó: K là trung điểm của AI
Đúng 0
Bình luận (1)
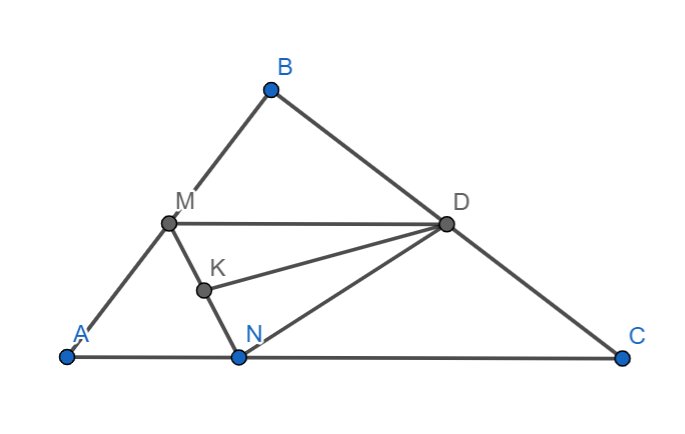
cho ΔABC có điểm M là trung điểm cạnh AC. Trên BM lấy điểm D sao cho DM=2.BM. Tia AD cắt BC tại K, cắt Bx tại E (Bx // AC)
a) tính tỉ số BE/AM
b) ΔBKE đồng dạng ΔCKA theo tỉ số đồng dạng là 1/4
c) tính tỉ số diện tích của ΔABK và ΔABC
Cho ΔABC lấy M là trung điểm của BC. CMinh :Nếu Â=90* thì AM=1/2 BC
1,Cho ΔABC có M,N theo thứ tự là trung điểm của AB và AC . Biết MN=4,5 cm. Tính CD=?
2,
Sửa đề: Tính BC
1: Xét ΔABC có
M là trung điểm của AB(gt)
N là trung điểm của AC(gt)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇔MN//BC và \(MN=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)
\(\Leftrightarrow BC=2\cdot MN=2\cdot4.5=9\left(cm\right)\)
Vậy: BC=9cm
Đúng 1
Bình luận (0)
Cho ΔABC. Gọi 2 điểm M, N thay đổi và thỏa mãn:
\(\overrightarrow{MN}=2\overrightarrow{MA}+\overrightarrow{MB}+3\overrightarrow{MC}\)
Chứng minh MN luôn đi qua 1 điểm cố định
1, cho ΔABC, trực tâm H. Đường vuông góc với AB tại B và đường vuông góc vói AC tại C cắt nhau bởi . M là trung điểm của BC, đường cao BN
a, BNCD là hình gì
b, Gọi O là trung điểm của AD. C/m OM=1/2 AH
2, cho ΔABC, các đường cao BD,CE cắt nhau tại H. Gọi I là trung điểm của AH, M là trung điểm của BC
a, C/m: lE=lD
b, C/m: D là điểm đối xứng với E qua lM
c, Góc lDM=?
Bài 2:
a: Ta có: ΔAEH vuông tại E
mà EI là đường trung tuyến
nên IE=AH/2(1)
Ta có: ΔADH vuông tại D
mà DI là đường trung tuyến
nên DI=AH/2(2)
Từ (1) và (2) suy ra IE=ID
b: Xét tứ giác BEDC có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
Do đó: BEDC là tứ giác nội tiếp đường tròn đường kính BC
=>ME=MD
hay M nằm trên đường trung trực của ED(1)
Ta có: IE=ID
nên I nằm trên đường trung trực của ED(2)
Từ (1) và (2) suy ra IM là đường trung trực của ED
hay D đối xứng với E qua IM
Đúng 0
Bình luận (0)
Cho ΔABC. Gọi M là trung điểm AB, D là trung điểm BC, N là điểm thuộc AC sao cho \(\overrightarrow{CN}\) = 2\(\overrightarrow{NA}\) . K là trung điểm MN. Chứng minh KD = \(\dfrac{1}{4}\)\(\overrightarrow{AB}\) + \(\dfrac{1}{3}\overrightarrow{AC}\).
Xét \(\Delta ABC\) có:
\(M\) là trung điểm \(AB\)
\(D\) là trung điểm \(BC\)
\(\Rightarrow\) \(MD\) là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\) \(MD\)\(=\)\(\dfrac{1}{2}AC\) và \(MD\) //\(AC\)
Ta có:
\(\overrightarrow{KD}=\overrightarrow{KM}+\overrightarrow{MD}\)
\(\Rightarrow\overrightarrow{KD}=\dfrac{1}{2}\overrightarrow{NM}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{KD}=\dfrac{1}{2}\overrightarrow{NA}+\dfrac{1}{2}\overrightarrow{AM}+\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{6}\overrightarrow{CA}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\\ \Rightarrow\overrightarrow{KD}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
Đúng 0
Bình luận (0)
Cho ΔABC có trọng tâm G, H là điểm đối xứng với B qua G, M là trung điểm BC.C/M 1) overrightarrow{AH} dfrac{2}{3}overrightarrow{AC}-dfrac{1}{3}overrightarrow{AB}2) overrightarrow{CH}-dfrac{1}{3}overrightarrow{AB}-dfrac{1}{3}overrightarrow{AC}3) overrightarrow{MH}dfrac{1}{6}overrightarrow{AC}-dfrac{5}{6}overrightarrow{AB}
Đọc tiếp
Cho ΔABC có trọng tâm G, H là điểm đối xứng với B qua G, M là trung điểm BC.
C/M 1) \(\overrightarrow{AH}\) = \(\dfrac{2}{3}\overrightarrow{AC}-\dfrac{1}{3}\overrightarrow{AB}\)
2) \(\overrightarrow{CH}=-\dfrac{1}{3}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}\)
3) \(\overrightarrow{MH}=\dfrac{1}{6}\overrightarrow{AC}-\dfrac{5}{6}\overrightarrow{AB}\)
H đối xứng B qua G \(\Rightarrow\overrightarrow{BH}=2\overrightarrow{BG}=2\left(\dfrac{1}{3}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}\right)=-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}\)
\(\overrightarrow{AH}=\overrightarrow{AB}+\overrightarrow{BH}=\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{3}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}=\dfrac{2}{3}\overrightarrow{AC}-\dfrac{1}{3}\overrightarrow{AB}\)
\(\overrightarrow{CH}=\overrightarrow{CA}+\overrightarrow{AH}=-\overrightarrow{AC}+\dfrac{2}{3}\overrightarrow{AC}-\dfrac{1}{3}\overrightarrow{AB}=-\dfrac{1}{3}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}\)
\(\overrightarrow{MH}=\overrightarrow{MA}+\overrightarrow{AH}=-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AC}+\dfrac{2}{3}\overrightarrow{AC}-\dfrac{1}{3}\overrightarrow{AB}\)
\(=-\dfrac{5}{6}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AC}\)
Đúng 1
Bình luận (0)