cho \(\Delta ABC\) có AB = 6cm, BC = 10cm, AC = 8cm tính độ dài trung tuyến AM của \(\Delta ABC\)

Những câu hỏi liên quan
Câu 8: Cho tam giác ABC vuông tại A , có AB = 6cm , AC = 8cm, AM là
đường trung tuyến ứng với cạnh BC . Độ dài của cạnh AM là :
A. 10cm
B. 9cm
C. 5cm
D. 8cm
Xét \(\Delta ABC\) vuông tại \(A\) có:
\(BC^2=AB^2+AC^2\) (định lí pitago)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét \(\Delta ABC\) vuông tại \(A\) có:
\(AM\) là đường trung tuyến ứng với cạnh huyền \(BC\) (định lí đường trung tuyến ứng với cạnh huyền trong tam giác vuông)
\(\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{1}{2}.10=5\left(cm\right)\)
\(\Rightarrow\) Chọn đáp án \(C\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tam giác \(ABC\) có \(AB = 6cm,AC = 8cm,BC = 10cm\). Đường phân giác của góc \(BAC\) cắt cạnh \(BC\) tại \(D\).
a) Tính độ dài các đoạn thẳng \(DB\) và \(DC\).
b) Tính tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\).
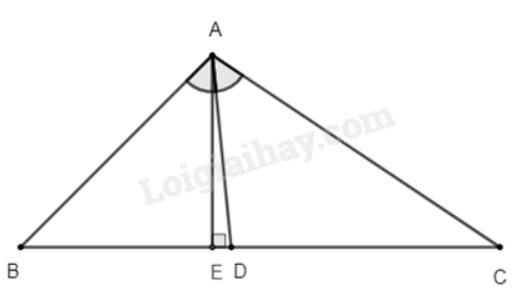
a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 10 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{10 - BD}} = \frac{6}{8} \Leftrightarrow 8BD = 6.\left( {10 - BD} \right) \Rightarrow 8BD = 60 - 6BD\)
\( \Leftrightarrow 8BD + 6BD = 60 \Leftrightarrow 14BD = 60 \Rightarrow BD = \frac{{60}}{{14}} = \frac{{30}}{7}\)
\( \Rightarrow DC = 10 - \frac{{30}}{7} = \frac{{40}}{7}\)
Vậy \(BD = \frac{{30}}{7}cm;DC = \frac{{40}}{7}cm\).
b) Kẻ \(AE \bot BC \Rightarrow AE\) là đường cao của tam giác \(ABC\).
Vì \(AE \bot BC \Rightarrow AE \bot BD \Rightarrow AE\)là đường cao của tam giác \(ADB\)
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = \frac{1}{2}BD.AE\)
Vì \(AE \bot BC \Rightarrow AE \bot DC \Rightarrow AE\)là đường cao của tam giác \(ADC\)
Diện tích tam giác \(ADC\) là:
\({S_{ADC}} = \frac{1}{2}DC.AE\)
Ta có: \(\frac{{{S_{ADB}}}}{{{S_{ADC}}}} = \frac{{\frac{1}{2}AE.BD}}{{\frac{1}{2}AE.CD}} = \frac{{BD}}{{DC}} = \frac{{\frac{{30}}{7}}}{{\frac{{40}}{7}}} = \frac{3}{4}\).
Vậy tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\) là \(\frac{3}{4}\).
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB AC 5cm, BC6cm . đường trung tuyến AM xuất phát từ đỉnh A của tam giác ABCa) Chứng minh Delta AMBDelta AMC và AM là tia phân của góc Ab) Chứng minh AM perp BCc) Tính độ dài các đoạn thẳng BM và AMd) Từ M vẽ ME perp AB ( E thuộc AB ) và MF perp AC ( F thuộc AC ) . Tam giác MEF là tam giác gì ? Vì saoai làm được mình cho 10000 sao
Đọc tiếp
Cho tam giác ABC có AB = AC = 5cm, BC=6cm . đường trung tuyến AM xuất phát từ đỉnh A của tam giác ABC
a) Chứng minh \(\Delta AMB=\Delta AMC\) và AM là tia phân của góc A
b) Chứng minh AM \(\perp\) BC
c) Tính độ dài các đoạn thẳng BM và AM
d) Từ M vẽ ME \(\perp\) AB ( E thuộc AB ) và MF \(\perp\) AC ( F thuộc AC ) . Tam giác MEF là tam giác gì ? Vì sao
ai làm được mình cho 10000 sao
a) Xét ΔABC có AB=AC=5
=> ΔABC cân tại A
ta có AM là trung tuyến => AM là đường phân giác của góc A (tc Δ cân)
=>\(\widehat{B}=\widehat{C}\)(tc)
Xét ΔABM và ΔACM có
AB=AC gt
có AM là trung tuyến => BM=CM
\(\widehat{B}=\widehat{C}\) (cmt)
=>ΔABM = ΔACM (cgc)
b) có ΔABC cân
mà AM là trung tuyến => AM là đường cao (tc Δ cân)
c) ta có AM là trung tuyến =>
M là trung điểm của BC
=> BM=CM=\(\dfrac{BC}{2}=\dfrac{6}{2}=3\)cm
Xét ΔABM có AM là đường cao => \(\widehat{AMB}=\)90o
=> AM2+BM2=AB2
=> AM2+32=52
=> AM =4 cm
d) Xét ΔBME và ΔCMF có
\(\widehat{MEB}=\widehat{MFC}=\)90o (ME⊥AB,MF⊥AC)
BM=CM (cmt)
\(\widehat{B}=\widehat{C}\)
=>ΔBME = ΔCMF (ch-cgv)
=>EM=FM( 2 góc tương ứng)
Xét ΔMEF có
EM=FM (cmt)
=> ΔMEF cân tại M
Đúng 2
Bình luận (1)
ai giúp mik bài này đc ko plsssssssssssssssss
Đúng 1
Bình luận (1)
Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm. Gọi AM là trung tuyến của tam giác
a) Chứng minh tam giác ABC vuông tại A. Tính độ dài AM
b) Kẻ MD vuông góc AB, ME vuông góc AC. Tứ giác ADME là hình gì? Vì sao
Vì AB^2 + AC^2 = BC^2 ( 6^2 + 8^2 = 10^2 )
=> ΔABC vuông tại A
a. Vì Am là trung tuyến của BC
=> AM =1/2 BC
=> AM = 5cm.
b. Xét tứ giác ADME, ta có:
góc DAE + góc AEM + góc EMD + góc MDA = 360°
=> 90° + 90° + góc EMD + 90° = 360°
=> góc EMD = 90°
=> Tứ giác ADME là hình chữ nhật.
Đúng 1
Bình luận (0)
Vì AB^2 + AC^2 = BC^2 ( 6^2 + 8^2 = 10^2 )
=> ΔABC vuông tại A
a. Vì Am là trung tuyến của BC
=> AM =1/2 BC
=> AM = 5cm.
b. Xét tứ giác ADME, ta có:
góc DAE + góc AEM + góc EMD + góc MDA = 360°
=> 90° + 90° + góc EMD + 90° = 360°
=> góc EMD = 90°
=> Tứ giác ADME là hình chữ nhật.
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Vẽ trung tuyến AM của tam giác.
Độ dài trung tuyến AM là:
A. 8cm
B.
54
cm
C.
44
cm
Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Vẽ trung tuyến AM của tam giác.Độ dài trung tuyến AM là:
A. 8cm
B.54cm
C.44cm
D. 6cm
Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Vẽ trung tuyến AM của tam giác.
Độ dài trung tuyến AM là:
A. 8cm
B.
54
cm
C.
44
cm
Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Vẽ trung tuyến AM của tam giác.Độ dài trung tuyến AM là:
A. 8cm
B.54cm
C.44cm
D. 6cm
Đúng 2
Bình luận (1)
Xem thêm câu trả lời
Cho \(\Delta ABC\) vuông tại A có AB= 6cm, BC= 10cm
Tính Ac và so sánh các góc \(\Delta ABC\)Trên tia đối của AB lấy D sao cho AD=AB. Gọi K là trung điểm của BC, đường thẳng DK cắt AC tại M.C/m BC=CD và độ dài AMĐường trung trức d của đoạn AC cẳ đường thẳng DC tại Q. C/m B, M, Q thẳng hànga] Áp dụng định lí Py - ta - go vào tam giác vuông ABC có ;
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\) \(AC^2=BC^2-AB^2\)
\(\Leftrightarrow\) \(AC^2=10^2-6^2\)
\(\Leftrightarrow\) \(AC^2=64\)
\(\Rightarrow\) \(AC=8cm\)
Ta có ; \(AB=6cm\) , \(AC=8cm\) , \(BC=10cm\)
\(\Rightarrow\) \(BC\)lớn hơn \(AC\) lớn hơn \(AB\)
\(\Leftrightarrow\) góc \(A\) lớn hơn góc \(B\) lớn hơn góc \(C\) [ theo quan hệ giữa cạnh và góc đối diện ]
Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm. Gọi AM là trung tuyết của tam giác ABC. Kẻ MD vuông góc AB, kẻ ME vuông góc AC. a) Chứng minh tam giác ABC vuông. b) Tính độ dài AM c) Tính độ dài DE d) Chứng minh tứ giác BDEC là hình thang e) Chứng minh tứ giác BDEM là hình bình hành f) Chứng minh tứ giác ADME là hình chữ nhật g) Khi AB = AC tứ giác ADME là hình gì ?
Cho \(\Delta ABC\) có \(\widehat{A}=120\) độ, AB = 4cm , AC = 6cm. Tính độ dài đường trung tuyến AM.
Cho tam giác vuông ABC có AB =6cm, AC=8cm, BC=10cm. Gọi AM là trung tuyến của tam giác.
a) Tính độ dài đoạn AM.
b) Kẻ MD vuông góc với AB, ME vuông góc với AC. Tứ giác ADME có dạng đặc biệt nào?
c) Tìm điều kiện của tam giác ABC để AEMD là hình vuông. Vẽ hình minh họa.
Xin lỗi vì mình không biết cách để đưa hình lên đây nhưng bạn có thể tự vẽ mà!!
a) Vì tam giác ABC vuông nên đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên
AM=\(\frac{BC}{2}=\frac{10}{2}=5\)
b) Tứ giác ADME là hình chữ nhật hay có 4 góc bằng nhau và bằng 90 độ
c) Giả sử AEMD là hình vuông
=> AE=AD
=>AC=AB
Vậy để AEMD là hình vuông thì tam giác ABC vuông cân
Đúng 0
Bình luận (0)
cam on ban da giup minh
Thank you very much!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời































