a) ĐKXĐ: \(x\notin\left\{1;-1\right\}\)

b) Ta có: \(P=\dfrac{2}{x^4-1}-\dfrac{1}{1-x^2}\)

\(=\dfrac{2}{\left(x^2-1\right)\left(x^2+1\right)}+\dfrac{1}{x^2-1}\)

\(=\dfrac{2+x^2-1}{\left(x^2-1\right)\left(x^2+1\right)}\)

\(=\dfrac{x^2+1}{\left(x^2-1\right)\left(x^2+1\right)}\)

\(=\dfrac{1}{x^2-1}\)

Đề sai rồi bạn

a) Ta có: x4 - 1 = (x2 + 1)(x2-1), trong đó : x2 + 1 > 0, với mọi x.

Vậy điều kiện : x2 – 1 ≠ 0

x2 – 1 = (x – 1)(x + 1) ≠ 0 ⇒ x ≠ ±1

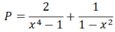
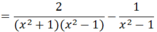
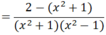
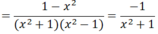
Do x2 + 1 > 0 với mọi x nên P < 0 với mọi x ≠ ±1

Xem lại biểu thức P.

Mình phải đi ăn nên chiều mình làm nốt câu d nhé

a) Điều kiện để P được xác định là: \(x\ne1;x\ne-1\)

b) \(P=\left(\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}\right):\dfrac{2x}{5x-5}x-\dfrac{x^2-1}{x^2+2x+1}\)

\(P=\left(\dfrac{\left(x+1\right)\left(x-1\right)-\left(x+1\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}\right):\dfrac{2x}{5x-5}x-\dfrac{\left(x+1\right)\left(x-1\right)}{\left(x+1\right)^2}\)

\(P=0:\dfrac{2x}{5x-5}x-\dfrac{x-1}{x+1}\)

\(P=-\dfrac{x-1}{x+1}\)

c) Theo đề ta có:

\(P=2\)

\(\Leftrightarrow-\dfrac{x-1}{x+1}=2\)

\(\Leftrightarrow-\left(x-1\right)=2x+2\)

\(\Leftrightarrow-x-2x=2-1\)

\(\Leftrightarrow-3x=1\)

\(\Leftrightarrow x=-\dfrac{1}{3}\)

d) \(P=-\dfrac{x-1}{x+1}\) nguyên khi:

\(\Leftrightarrow x-1⋮-\left(x+1\right)\)

\(\Leftrightarrow\left(x+1\right)-2⋮-\left(x+1\right)\)

\(\Leftrightarrow-2⋮-\left(x+1\right)\)

\(\Leftrightarrow2⋮x+1\)

\(\Rightarrow x+1\inƯ\left(2\right)\)

Vậy \(P\) nguyên khi \(x\in\left\{-2;0;-3;1\right\}\)

a) A =  \(\dfrac{1}{x-1}-\dfrac{4}{x+1}+\dfrac{8x}{\left(x-1\right)\left(x+1\right)}\) 

= \(\dfrac{x+1-4x+4+8x}{\left(x-1\right)\left(x+1\right)}=\dfrac{5x+5}{\left(x-1\right)\left(x+1\right)}=\dfrac{5}{x-1}\) => đpcm

b) \(\left|x-2\right|=3=>\left[{}\begin{matrix}x-2=3< =>x=5\left(C\right)\\x-2=-3< =>x=-1\left(L\right)\end{matrix}\right.\)

Thay x = 5 vào A, ta có:

A = \(\dfrac{5}{5-1}=\dfrac{5}{4}\)

c) Để A nguyên <=> \(5⋮x-1\)

a)

A=\(\left(\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}\right)\div\dfrac{2x}{5x-5}\)

\(\Leftrightarrow\left(\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}\right)\div\dfrac{2x}{5\left(x-1\right)}\)

ĐKXĐ: \(\left\{{}\begin{matrix}x-1\ne0\\x+1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0+1\\x=0-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

MTC: 5(x-1)(x+1)

\([\dfrac{5\left(x+1\right)\left(x+1\right)}{5\left(x-1\right)\left(x+1\right)}-\dfrac{5\left(x-1\right)\left(x-1\right)}{5\left(x-1\right)\left(x+1\right)}]\div\dfrac{2x\left(x+1\right)}{5\left(x-1\right)\left(x+1\right)}\)

\(\Rightarrow[5\left(x+1\right)\left(x+1\right)-5\left(x-1\right)\left(x-1\right)]\div2x\left(x+1\right)\)

\(\Leftrightarrow[5\left(x+1\right)^2-5\left(x-1\right)^2]\div2x^2+2x\)

\(\Leftrightarrow[5\left(x^2+2x+1\right)-5\left(x^2-2x+1\right)]\div2x^2+2x\)

\(\Leftrightarrow(5x^2+10x+5-5x^2+10x-5)\div2x^2+2x\)

\(\Leftrightarrow20x\div\left(2x^2+2x\right)\)

\(\Leftrightarrow10x+10\)

a)  \(A= \dfrac{1}{x-2}+\dfrac{1}{x+2}+\dfrac{x^2+1}{x^2-4} \\ =\dfrac{1}{x-2}+\dfrac{1}{x-2}+\dfrac{x^2+1}{(x-2)(x+2)} \\= \dfrac{x+2+x-2+x^2+1}{(x-2)(x+2)} \\=\dfrac{x^2+2x+1}{x^2-4} \\ =\dfrac{(x+1)^2}{(x-2)(x+2)}\)

b) Với mọi \(x\) thỏa mãn \(-2<x<2\) và \(x \ne -1\) thì \(x-2\) đều có giá trị âm, mà \(\begin{cases}(x+1)^2≥0\\x+2>0\\\end{cases}\) \( \Rightarrow\) Biểu thức A luôn có giá trị âm.

\(A=\dfrac{x+2+x-2+x^2+1}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x+1\right)^2}{\left(x-2\right)\left(x+2\right)}\)

Với \(-2< x< 2\Leftrightarrow\left\{{}\begin{matrix}x-2< 0\\x+2>0\end{matrix}\right.\Leftrightarrow\left(x-2\right)\left(x+2\right)< 0;x\ne-1\Leftrightarrow\left(x+1\right)^2>0\Leftrightarrow A< 0\)

\(A=\dfrac{x+2+x-2+x^2+1}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+2x+1}{x^2-4}\)

Bài 1: ĐKXĐ:`x + 3 ne 0` và `x^2+ x-6 ne 0 ; 2-x ne 0`

`<=> x ne -3 ; (x-2)(x+3) ne 0 ; x ne2`

`<=>x ne -3 ; x ne 2`

b) Với `x ne - 3 ; x ne 2` ta có:

`P= (x+2)/(x+3)  - 5/(x^2 +x -6) + 1/(2-x)`

`P = (x+2)/(x+3) - 5/[(x-2)(x+3)] + 1/(2-x)`

`= [(x+2)(x-2)]/[(x-2)(x+3)] - 5/[(x-2)(x+3)] - (x+3)/[(x-2)(x+3)]`

`= (x^2 -4)/[(x-2)(x+3)] - 5/[(x-2)(x+3)] - (x+3)/[(x-2)(x+3)]`

`=(x^2 - 4 - 5 - x-3)/[(x-2)(x+3)]`

`= (x^2 - x-12)/[(x-2)(x+3)]`

`= [(x-4)(x+3)]/[(x-2)(x+3)]`

`= (x-4)/(x-2)`

Vậy `P= (x-4)/(x-2)` với `x ne -3 ; x ne 2`

c) Để `P = -3/4`

`=> (x-4)/(x-2) = -3/4`

`=> 4(x-4) = -3(x-2)`

`<=>4x -16 = -3x + 6`

`<=> 4x + 3x = 6 + 16`

`<=> 7x = 22`

`<=> x= 22/7` (thỏa mãn ĐKXĐ)

Vậy `x = 22/7` thì `P = -3/4`

d) Ta có: `P= (x-4)/(x-2)`

`P= (x-2-2)/(x-2)`

`P= 1 - 2/(x-2)`

Để P nguyên thì `2/(x-2)` nguyên

`=> 2 vdots x-2`

`=> x -2 in Ư(2) ={ 1 ;2 ;-1;-2}`

+) Với `x -2 =1 => x= 3` (thỏa mãn ĐKXĐ)

+) Với `x -2 =2 => x= 4`  (thỏa mãn ĐKXĐ)

+) Với `x -2 = -1=> x= 1` (thỏa mãn ĐKXĐ)

+) Với `x -2 = -2 => x= 0`(thỏa mãn ĐKXĐ)

Vậy `x in{ 3 ;4; 1; 0}` thì `P` nguyên

e) Từ `x^2 -9 =0`

`<=> (x-3)(x+3)=0`

`<=> x= 3` hoặc `x= -3`

+) Với `x=3` (thỏa mãn ĐKXĐ) thì:

`P  = (3-4)/(3-2)`

`P= -1/1`

`P=-1`

+) Với `x= -3` thì không thỏa mãn ĐKXĐ

Vậy với x= 3 thì `P= -1`