Giải phương trình
4x^3-16x=0
Giải các bất phương trình mũ sau: 16 x - 4 x - 6 ≤ 0
Đặt t = 4 x (t > 0), ta có hệ bất phương trình:
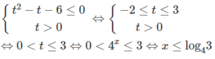
giải các phương trình:
(3 - x)^2 - 12 + 4x = 0
(4x - 5)^2 - 2 (16x^2 - 25) = 0
GIÚP MK VỚI :<<
\(a.\left(3-x\right)^2-12+4x=0\)
\(\Rightarrow\left(3-x\right)^2-4.\left(3-x\right)=0\)
\(\Rightarrow\left(3-x\right)\left(-x-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}3-x=0\\-x-1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=3\\x=-1\end{cases}}\)
\(b.\left(4x-5\right)^2-2.\left(16x^2-25\right)=0\)
\(\Rightarrow\left(4x-5\right)^2-2.\left(4x+5\right).\left(4x-5\right)=0\)
\(\Rightarrow\left(4x-5\right)\left(4x-5-8x-10\right)=0\)
\(\Rightarrow\left(4x-5\right)\left(-4x-15\right)=0\)
\(\Rightarrow\orbr{\begin{cases}4x-5=0\\-4x-15=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{5}{4}\\x=\frac{-15}{4}\end{cases}}\)
Giải các phương trình sau:
\(a.\left(x^2-2x\right)^2-2\left(x^2-2x\right)-3=0\)
\(b.\left(x^2+4x+2\right)^2+4x^2+16x+11=0\)
a) Ta có: \(\left(x^2-2x\right)^2-2\left(x^2-2x\right)-3=0\)
\(\Leftrightarrow\left(x^2-2x\right)^2+\left(x^2-2x\right)-3\left(x^2-2x\right)-3=0\)
\(\Leftrightarrow\left(x^2-2x\right)\left(x^2-2x+1\right)-3\left(x^2-2x+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2\cdot\left(x^2-2x-3\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2\cdot\left(x+1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=3\end{matrix}\right.\)
Vậy: S={1;-1;3}
giải các phương trình sau bằng cách đưa về phương trình tích
a) x^2+10x+25-4x(x+5)=0
b) (4x-5)^2-2(16x^2-25)=0
Tham khảo bài này :
(3x+1)(7x+3)=(5x-7)(3x+1)
<=> (3x+1)(7x+3)-(5x-7)(3x+1)=0
<=> (3x+1)(7x+3-5x+7)=0
<=> (3x+1)(2x+10)=0
<=> 2(3x+1)(x+5)=0
=> 3x+1=0 hoặc x+5=0
=> x= -1/3 hoặc x=-5
Vậy x = -1/3 hoặc x = -5
\(a,x^2+10x+25-4x\left(x+5\right)=0.\)
\(\Leftrightarrow\left(x+5\right)^2-4x\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(5-3x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\5-3x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=\frac{5}{3}\end{cases}}}\)
\(b,\left(4x-5\right)^2-2\left(16x^2-25\right)=0\)
\(\Leftrightarrow\left(4x-5\right)^2-2\left(4x+5\right)\left(4x-5\right)=0\)
\(\Leftrightarrow-\left(4x-5\right)\left(4x+15\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}4x-5=0\\4x+15=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{5}{4}\\x=-\frac{15}{4}\end{cases}}}\)
giải phương trình :\(4x^3+4x^2-5x+9=4\sqrt[4]{16x+8}\)
ĐKXĐ: \(x\ge-\dfrac{1}{2}\)
\(4x^3+4x^2-5x+9=4\sqrt[4]{\left(2x+1\right).2.2.2}\le2x+1+2+2+2\)
\(\Leftrightarrow4x^3+4x^2-7x+2\le0\)
\(\Leftrightarrow\left(x+2\right)\left(2x-1\right)^2\le0\)
\(\Leftrightarrow\left(2x-1\right)^2\le0\) (do \(x+2>0\) ; \(\forall x\ge-\dfrac{1}{2}\))
\(\Rightarrow x=\dfrac{1}{2}\)
Vậy pt có nghiệm duy nhất \(x=\dfrac{1}{2}\)
Giải phương trình:
\(4x^2-6x+1=-\dfrac{\sqrt{3}}{3}.\sqrt{16x^4+4x^2+1}\)
Ta có:
\(16x^4+4x^2+1=16x^4+8x^2+1-4x^2=\left(4x^2+1\right)^2-4x^2=\left(4x^2-2x+1\right)\left(4x^2+2x+1\right)\)
\(4x^2-6x+1=2\left(4x^2-2x+1\right)-\left(4x^2+2x+1\right)\)
Chia hai vế phương trình ban đầu cho \(4x^2+2x+1\) ta được
\(2\dfrac{4x^2-2x+1}{4x^2+2x+1}-1=\dfrac{-\sqrt{3}}{3}\sqrt{\dfrac{4x^2-2x+1}{4x^2+2x+1}}\)
Đặt \(y=\sqrt{\dfrac{4x^2-2x+1}{4x^2+2x+1}}>0\), phương trình trên tương đương với
\(2y^2-1=\dfrac{-\sqrt{3}}{3}y\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{\sqrt{3}}{3}\left(tm\right)\\y=\dfrac{-\sqrt{3}}{2}\left(l\right)\end{matrix}\right.\)
Với \(y=\dfrac{\sqrt{3}}{3}\) ta có:
\(\dfrac{4x^2-2x+1}{4x^2+2x+1}=\dfrac{1}{3}\Leftrightarrow3\left(4x^2-2x+1\right)-\left(4x^2+2x+1\right)=0\)
\(\Leftrightarrow x=\dfrac{1}{2}\).
giải phương trình
1)\(\sqrt{9\left(x-1\right)}=21\)
2)\(\sqrt{1-x}+\sqrt{4-4x}-\dfrac{1}{3}\sqrt{16-16x}+5=0\)
3)\(\sqrt{2x}-\sqrt{50}=0\)
4)\(\sqrt{4x^2+4x+1}=6\)
5)\(\sqrt{\left(x-3\right)^2}=3-x\)
1) \(\sqrt[]{9\left(x-1\right)}=21\)
\(\Leftrightarrow9\left(x-1\right)=21^2\)
\(\Leftrightarrow9\left(x-1\right)=441\)
\(\Leftrightarrow x-1=49\Leftrightarrow x=50\)
2) \(\sqrt[]{1-x}+\sqrt[]{4-4x}-\dfrac{1}{3}\sqrt[]{16-16x}+5=0\)
\(\Leftrightarrow\sqrt[]{1-x}+\sqrt[]{4\left(1-x\right)}-\dfrac{1}{3}\sqrt[]{16\left(1-x\right)}+5=0\)
\(\)\(\Leftrightarrow\sqrt[]{1-x}+2\sqrt[]{1-x}-\dfrac{4}{3}\sqrt[]{1-x}+5=0\)
\(\Leftrightarrow\sqrt[]{1-x}\left(1+3-\dfrac{4}{3}\right)+5=0\)
\(\Leftrightarrow\sqrt[]{1-x}.\dfrac{8}{3}=-5\)
\(\Leftrightarrow\sqrt[]{1-x}=-\dfrac{15}{8}\)
mà \(\sqrt[]{1-x}\ge0\)
\(\Leftrightarrow pt.vô.nghiệm\)
3) \(\sqrt[]{2x}-\sqrt[]{50}=0\)
\(\Leftrightarrow\sqrt[]{2x}=\sqrt[]{50}\)
\(\Leftrightarrow2x=50\Leftrightarrow x=25\)
1) \(\sqrt{9\left(x-1\right)}=21\) (ĐK: \(x\ge1\))
\(\Leftrightarrow3\sqrt{x-1}=21\)
\(\Leftrightarrow\sqrt{x-1}=7\)
\(\Leftrightarrow x-1=49\)
\(\Leftrightarrow x=49+1\)
\(\Leftrightarrow x=50\left(tm\right)\)
2) \(\sqrt{1-x}+\sqrt{4-4x}-\dfrac{1}{3}\sqrt{16-16x}+5=0\) (ĐK: \(x\le1\))
\(\Leftrightarrow\sqrt{1-x}+2\sqrt{1-x}-\dfrac{4}{3}\sqrt{1-x}+5=0\)
\(\Leftrightarrow\dfrac{5}{3}\sqrt{1-x}+5=0\)
\(\Leftrightarrow\dfrac{5}{3}\sqrt{1-x}=-5\) (vô lý)
Phương trình vô nghiệm
3) \(\sqrt{2x}-\sqrt{50}=0\) (ĐK: \(x\ge0\))
\(\Leftrightarrow\sqrt{2x}=\sqrt{50}\)
\(\Leftrightarrow2x=50\)
\(\Leftrightarrow x=\dfrac{50}{2}\)
\(\Leftrightarrow x=25\left(tm\right)\)
4) \(\sqrt{4x^2+4x+1}=6\)
\(\Leftrightarrow\sqrt{\left(2x+1\right)^2}=6\)
\(\Leftrightarrow\left|2x+1\right|=6\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=6\left(ĐK:x\ge-\dfrac{1}{2}\right)\\2x+1=-6\left(ĐK:x< -\dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=5\\2x=-7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\left(tm\right)\\x=-\dfrac{7}{2}\left(tm\right)\end{matrix}\right.\)
5) \(\sqrt{\left(x-3\right)^2}=3-x\)
\(\Leftrightarrow\left|x-3\right|=3-x\)
\(\Leftrightarrow x-3=3-x\)
\(\Leftrightarrow x+x=3+3\)
\(\Leftrightarrow x=\dfrac{6}{2}\)
\(\Leftrightarrow x=3\)
1) => 9(x-1)=\(21^2\)
=> 9x-9=441
=> 9x=450
=> x=50
2)=>\(\sqrt{1-x}\) + \(\sqrt{4\left(1-x\right)}\)-\(\dfrac{1}{3}\sqrt{16\left(1-x\right)}\)+5=0
=>\(\sqrt{1-x}\)\(\left(1+2-\dfrac{1}{3}.4\right)\)+5=0
=>\(\dfrac{5}{3}\sqrt{1-x}\) +5=0
=>\(\sqrt{1-x}\)=-3
Phuong trinh vo nghiem
Bài 3.giải các phương trình sau bằng cách đưa về phương trình tích.
a) (3x+1)(7x+3)=(5x-7)(3x+1)
b) x^2+10x+25-4x(x+5)=0
c) (4x-5)^2(16x^2-25)=0
d) (4x+3)^2=4(x^2-2x+1)
e) x^2-11x=28=0
f) 3x^3-3x^2-6x=0
1/ Chứng minh phương trình vô nghiệm:
a) \(-16x^2-8x+4=0\)
b) \(-x^2+4x-4=0\)
2/ Giải phương trình sau:
\(\left(x^2-2x-4\right)\left(2x^2-8x-1\right)=0\)
Bài 1:
b: \(\Leftrightarrow x-2=0\)
hay x=2