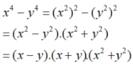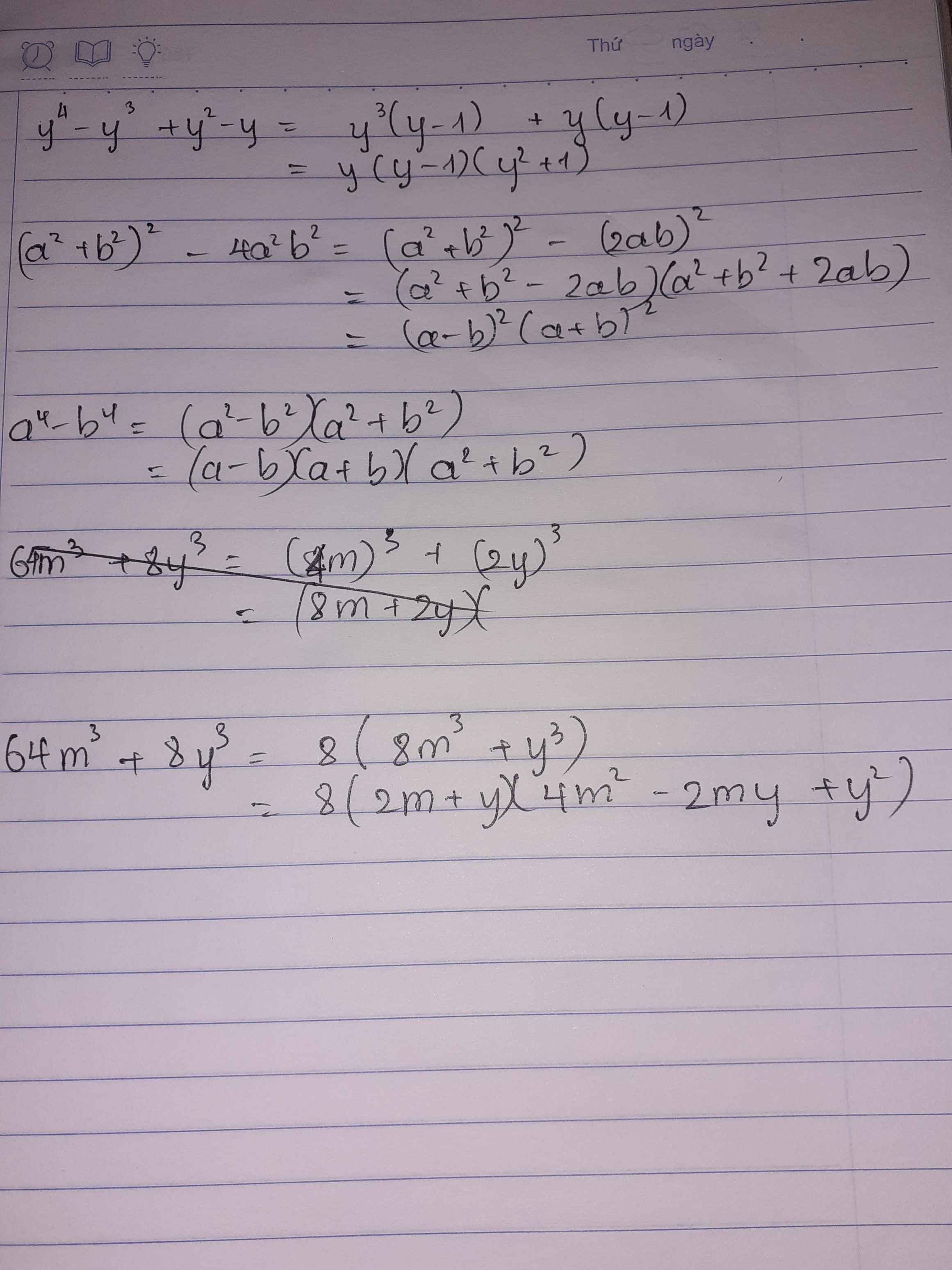Phân Tích đa thức thành nhân tử 4x4 _ 21x2y2 + y4

Những câu hỏi liên quan
phân tích đa thức thành nhân tửa,6x2 + 7xy + 2y2 b,) x2 – y2 + 10x – 6y + 16 c,4x4 + y4
Đọc tiếp
phân tích đa thức thành nhân tử
a,6x2 + 7xy + 2y2
b,) x2 – y2 + 10x – 6y + 16
c,4x4 + y4
a) 6x² + 7xy + 2y²
= 6x² + 4xy + 3xy + 2y²
= (6x² + 4xy) + (3xy + 2y²)
= 2x(3x + 2y) + y(3x + 2y)
= (3x + 2y)(2x + y)
b) x² - y² + 10x - 6y + 16
= x² + 10x + 25 - y² - 6y - 9
= (x² + 10x + 25) - (y² + 6y + 9)
= (x + 5)² - (y + 3)²
= (x + 5 - y - 3)(x + 5 + y + 3)
= (x - y + 2)(x + y + 8)
c) 4x⁴ + y⁴
= 4x⁴ + 4x²y² + y⁴ - 4x²y²
= (2x² + y²)² - (2xy)²
= (2x² + y² - 2xy)(2x² + y² + 2xy)
Đúng 0
Bình luận (0)
64x4+y4 phân tích đa thức thành nhân tử
Đọc tiếp
64x4+y4 phân tích đa thức thành nhân tử
64x^4+y^4
=64x^4+16x^2y^2+y^4-16x^2y^2
=(8x^2+y^2)^2-(4xy)^2
=(8x^2-4xy+y^2)(8x^2+4xy+y^2)
Đúng 0
Bình luận (0)
Phần tự luận (8 điểm)
Phân tích thành nhân tử
a ) x 6 – x 4 + 2 x 3 + 2 x 2 b ) 4 x 4 + y 4
a) x6 – x4 + 2x3 + 2x2
= x2(x4 – x2 + 2x + 2)
= x2[x2(x2 – 1) + 2(x + 1)]
= x2. [x2.(x -1).(x + 1) + 2(x+ 1)]
= x2 (x+ 1).[x2(x- 1)+ 2]
= x2(x + 1)(x3 – x2 + 2)
= x2(x + 1)[(x3 + 1) – (x2 – 1)]
= x2(x + 1).[(x + 1).(x2 – x + 1) - (x - 1).(x + 1)]
= x2(x + 1)(x + 1)( x2 – x + 1 – x + 1)
= x2(x + 1)2(x2 – 2x + 2).
b) 4x4 + y4 = 4x4 + 4x2y2 + y4 - 4x2y2
= (2x2 + y2)2 - (2xy)2
= (2x2 + y2 + 2xy)(2x2 + y2 - 2xy)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử: x4 +x2y2+y4
x⁴ + x²y² +y⁴
= (x²)² + x²y² + (y²)²
= (x²)² + x²y² + (y²)² + x²y² - x²y²
= (x²)² + 2 x²y² + (y²)² - x²y²
= (x² + y²)²- (xy)²
=(x² + y² + xy)(x² + y² - xy)
Đúng 2
Bình luận (0)
Phân tích các đa thức sau thành nhân tử: c ) x 4 - y 4
x^4-y^4=(x^2-y^2)(x^2+y^2)=(x-y)(x+y)(x^2+y^2)
Phân tích các đa thức sau thành nhân tử :
i/ x2+5x−6x2+5x−6
m/ 6x2−7x+26x2−7x+2
n/ 4x4+81
a: =(x+6)(x-1)
n: \(=4x^4+36x^2+81-36x^2\)
\(=\left(2x^2+9-6x\right)\left(2x^2+9+6x\right)\)
Đúng 1
Bình luận (0)
phân tích đa thức thành nhân tử
y4-y3+y2-y
(a2+b2)2 - 4a2b2
a4- b4
64m3+8y3
b) \(\left(a^2+b^2\right)^2-4a^2b^2\)
\(=\left(a^2-2ab+b^2\right)\left(a^2+2ab+b^2\right)\)
\(=\left(a-b\right)^2\cdot\left(a+b\right)^2\)
c) \(a^4-b^4=\left(a-b\right)\left(a+b\right)\left(a^2+b^2\right)\)
Đúng 0
Bình luận (0)
a) \(y^4-y^3+y^2-y\)
\(=y^3\left(y-1\right)+y\left(y-1\right)\)
\(=y\left(y-1\right)\left(y^2+1\right)\)
d) \(64m^3+8y^3=\left(4m+2y\right)\left(16m^2-8my+4y^2\right)\)
Đúng 0
Bình luận (0)
BÀi 1: Phân tích đa thức thành nhân tử
a)x3+8x2+17x+10
b)abc+ab+bc+ca+a+b+c+1
c)4x4+81
d)64x4+y4
e)x5+x4+1
f)x+2y-xy-2
g)a2+b2-x2-y2+2ab-2xy
a. = \(\left(x^3+x^2\right)+\left(7x^2+7x\right)+\left(10x+10\right)\)
= \(x^2\left(x+1\right)+7x\left(x+1\right)+10x\left(x+1\right)\)
= \(\left(x+1\right)\left(x^2+7x+10x\right)\)
= \(\left(x+1\right)\left(x+2\right)\left(x+5\right)\)
Đúng 0
Bình luận (0)
Toán vận dụng: phân tích đa thức: x4-y4+2x3y-2xy3 thành nhân tử (x+y).(x2-y2)
\(x^4-y^4+2x^3y-2xy^3\)
\(=\left(x^2+y^2\right)\left(x^2-y^2\right)+2xy\left(x^2-y^2\right)\)
\(=\left(x^2-y^2\right)\left(x^2+y^2+2xy\right)\)
\(=\left(x-y\right)\left(x+y\right)\left(x+y\right)^2\)
\(=\left(x-y\right)\left(x+y\right)^3\)
Đúng 0
Bình luận (1)
\(x^4-y^4+2x^3y-2xy^3\\ =\left(x^2\right)^2-\left(y^2\right)^2+2xy\left(x^2-y^2\right)\\ =\left(x^2-y^2\right)\left(x^2+y^2\right)+2xy\left(x^2-y^2\right)\\ =\left(x^2-y^2\right)\left(x^2+y^2+2xy\right)\\ =\left(x-y\right)\left(x+y\right)\left(x+y\right)^2\\ =\left(x-y\right)\left(x+y\right)^3\)
Đúng 0
Bình luận (2)
Phân tích các đa thức sau thành nhân tử rồi tính giá trị đa thức:a) A 9x2 + 15x + 6xy + y2 + 5y biết 3x + y 0b) B 25x2 – y4 – 5x + y2
Đọc tiếp
Phân tích các đa thức sau thành nhân tử rồi tính giá trị đa thức:
a) A = 9x2 + 15x + 6xy + y2 + 5y biết 3x + y = 0
b) B = 25x2 – y4 – 5x + y2
Lời giải:
a. $A=9x^2+15x+6xy+y^2+5y=(9x^2+6xy+y^2)+(15x+5y)$
$=(3x+y)^2+5(3x+y)=0^2+5.0=0$
b. $25x^2-y^4-5x+y^2=(25x^2-y^4)-(5x-y^2)=(5x-y^2)(5x+y^2)-(5x-y^2)$
$=(5x-y^2)(5x+y^2-1)$
Đúng 0
Bình luận (0)