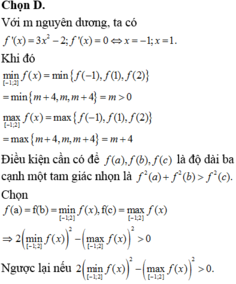Cho a, b, c là độ dài ba cạnh của một tam giác, với thì (a+b+c)^2<=9bc

Những câu hỏi liên quan
Chứng minh rằng nếu a + b , b + c , c + a là độ dài ba cạnh của một tam giác thì \(\frac{1}{a+b},\frac{1}{b+c},\frac{1}{c+a}\) cũng là độ dài 3 cạnh của một tam giác
Ta có : a+b > c , b+c > a , c+a > b
Xét : \(\frac{1}{a+c}+\frac{1}{b+c}>\frac{1}{a+b+c}+\frac{1}{b+c+a}=\frac{2}{a+b+c}>\frac{2}{a+b+a+b}=\frac{1}{a+b}\)
Tương tự , ta cũng có : \(\frac{1}{a+b}+\frac{1}{b+c}>\frac{1}{a+c};\frac{1}{a+b}+\frac{1}{a+c}>\frac{1}{b+c}\)
Vậy ta có đpcm
Chú ý : a,b,c là độ dài ba cạnh của một tam giác chứ không phải a+b,b+c,c+a nhé :)
Đúng 0
Bình luận (0)
Viết chương trình nhập từ bàn phím 3 số thực a, b, c. Kiểm tra nếu a, b, c có là độ dài 3 cạnh của một tam giác cân thì đưa ra thông điệp "Ba số đã nhập là độ dài 3 cạnh của một tam giác cân". Giúp em với ạ :((
#include <bits/stdc++.h>
using namespace std;
int main() {
double a, b, c;
cin >> a >> b >> c;
if(a==b)
{if (b!=c) {cout << "Ba so da nhap la do dai ba canh cua mot tam giac can";}
if(b==c) {cout << "Ba so da nhap la do dai ba canh cua mot tam giac deu";}}
if(b==c)
{if(a!=b) {cout << "Ba so da nhap la do dai ba canh cua mot tam giac can";}}
if(a==c)
{if(a!=b) {cout << "Ba so da nhap la do dai ba canh cua mot tam giac can";}}
if(a!=b)
{if(b!=c) {cout << "Ba so da nhap khong la do dai ba canh cua mot tam giac can";}}
return 0;
}
Chúc bn học tốt! (Bonus thêm trường hợp không là độ dài tam giác cân và là độ dài của tam giác đều nha!)
Đúng 0
Bình luận (0)
1, Áp dụng định lý Pytago. Chứng minh rằng nếu ta có a, b, c 0 sao cho a m2 + n2 ; b m2 - n2 ; c 2mn thì a, b, c là số đo 3 cạnh của tam giác vuông.2, Các ạnh góc vuông của một tam giác vuông có độ dài a, b và diện tích bằng S. Tính các góc của tam giác vuông đó biết (a + b)23, Chứng minh rằng nếu a, b, c là độ dài ba cạnh của 1 tam giác vuông (với a là độ dài cạnh huyền) thì các số x, y, z sau đây cũng là độ dài cạnh của tam giác vuông: x 9a + 4b +8c ; y 4a + b+ 4c ; z 8a + 4b + 7c
Đọc tiếp
1, Áp dụng định lý Pytago. Chứng minh rằng nếu ta có a, b, c > 0 sao cho a = m2 + n2 ; b = m2 - n2 ; c = 2mn thì a, b, c là số đo 3 cạnh của tam giác vuông.
2, Các ạnh góc vuông của một tam giác vuông có độ dài a, b và diện tích bằng S. Tính các góc của tam giác vuông đó biết (a + b)2
3, Chứng minh rằng nếu a, b, c là độ dài ba cạnh của 1 tam giác vuông (với a là độ dài cạnh huyền) thì các số x, y, z sau đây cũng là độ dài cạnh của tam giác vuông: x = 9a + 4b +8c ; y = 4a + b+ 4c ; z = 8a + 4b + 7c
Cho hàm số f(x) x3-3x+m+2 Có bao nhiêu số nguyên dương m 2018 sao cho với mọi bộ ba số thực
a
,
b
,
c
∈
-
1
;
3
thì f(a), f(b), f(c) là độ dài ba cạnh của một tam giác nhọn A. 2009 B. 2013 C. 2017 D. 2008
Đọc tiếp
Cho hàm số f(x)= x3-3x+m+2 Có bao nhiêu số nguyên dương m < 2018 sao cho với mọi bộ ba số thực a , b , c ∈ - 1 ; 3 thì f(a), f(b), f(c) là độ dài ba cạnh của một tam giác nhọn
A. 2009
B. 2013
C. 2017
D. 2008
Cho a,b,c là độ dài ba cạnh của một tam giác vuông(c là độ dài cạnh huyền).Chứng minh rằng a^2020+b^2020<c^2020
Gọi a,b,c là độ dài ba cạnh của một tam giác. Cho biết (a+b)(b+c)(c+a)=8abc. CM: tam giác đã cho là tam giác đều
a;b;c là 3 cạnh của tam giác => a; b; c dương
Với a; b dương ta có: \(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\) => a + b \(\ge\) 2. \(\sqrt{ab}\)
Tương tự, b + c \(\ge\) 2.\(\sqrt{bc}\); c + a \(\ge\)2. \(\sqrt{ca}\)
=> (a + b).(b+c).(c+a) \(\ge\)8. \(\sqrt{ab}\).\(\sqrt{bc}\).\(\sqrt{ca}\) = 8.abc
Dấu = xảy ra khi a = b = c
=> tam giác có 3 cạnh là a; b; c là tam giác đều
Đúng 0
Bình luận (0)
Câu3 (2 điểm):
a) Cho a, b, c là độ dài ba cạnh của tam giác có chu vi bằng 2.
Chứng minh: (a + b + c)^2 - (a^2 + b^2 + c^2) - 2abc > 2
b) Chứng minh nếu a, b, c và a', b', c' là độ dài các cạnh của hai tam giác
đồng dạng thì: aa' + bb' + cc' = (a + b + c) (a' + b' + c')
Gọi a,b,c là độ dài ba cạnh của một tam giác. Cho biết (a+b)(b+c)(c+a)=8abc. CM: tam giác đã cho là tam giác đều bât
Với a,b,c là độ dài ba cạnh của một tam giác, cmr 3/(b+c-a)+4/(c+a-b)+5/(a+b-c)≥6/a+4/b+2/c
\(A=\dfrac{3}{b+c-a}+\dfrac{4}{c+a-b}+\dfrac{5}{a+b-c}\)
\(=\dfrac{3}{c+a-b}+\dfrac{3}{a+b-c}+\dfrac{2}{b+c-a}+\dfrac{2}{a+b-c}+\dfrac{1}{b+c-a}+\dfrac{1}{c+a-b}\)
\(=3\left(\dfrac{1}{c+a-b}+\dfrac{1}{a+b-c}\right)+2\left(\dfrac{1}{b+c-a}+\dfrac{1}{a+b-c}\right)+\dfrac{1}{b+c-a}+\dfrac{1}{c+a-b}\)
\(do\) \(a,b,c\) \(là\) \(độ\) \(dài\) \(3\) \(cạnh\) \(\Delta\Rightarrow a,b,c\) \(không\) \(âm\) \(\)
\(và\left\{{}\begin{matrix}b+c-a>0\\c+a-b>0\\a+b-c>0\end{matrix}\right.\) \(\Rightarrowáp\) \(dụng\) \(Am-GM\)
\(\Rightarrow\left\{{}\begin{matrix}3\left(\dfrac{1}{c+a-b}+\dfrac{1}{a+b-c}\right)\ge3.\dfrac{4}{c+a-b+a+b-c}\ge\dfrac{12}{2a}\ge\dfrac{6}{a}\\2\left(\dfrac{1}{b+c-a}+\dfrac{1}{a+b-c}\right)\ge2.\dfrac{4}{b+c-a+a+b-c}\ge\dfrac{8}{2b}\ge\dfrac{4}{b}\\\dfrac{1}{b+c-a}+\dfrac{1}{c+a-b}\ge\dfrac{4}{b+c-a+c+a-b}\ge\dfrac{4}{2c}\ge\dfrac{2}{c}\\\end{matrix}\right.\)
\(\Rightarrow A\ge\dfrac{6}{a}+\dfrac{4}{b}+\dfrac{2}{c}\)
Đúng 1
Bình luận (0)