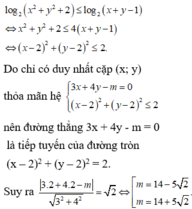Tìm tất cả các cặp (x;y) nguyên dương sao cho \(x^2y^4-y^3+1\)là số chính phương

Những câu hỏi liên quan
1)Tim tất cả các cặp số nguyên x,y thỏa mãn :(x+5)y-x=10
2)Tìm tất cả các cặp số nguyên c,d để tích của chúng bằng 5 lần tổng của chúng
tớ chỉ làm phần 1 thôi
1. ta có (x+5)y-x=10
=>(x+5)y-x-5=10-5
=>(x+5)y-(x+5)=5
=>(x+5)(y-1)=5
lập bảng xét giá trị của x,y \(\in Z\)
Bạn tự làm tiếp nhé -_-
Đúng 2
Bình luận (0)
Biết rằng trong tất cả các cặp (x; y) thỏa mãn:
log
2
x
2
+
y
2
+
2
≤
log
2
x
+
y
-
1...
Đọc tiếp
Biết rằng trong tất cả các cặp (x; y) thỏa mãn: log 2 x 2 + y 2 + 2 ≤ log 2 x + y - 1 . Chỉ có duy nhất một cặp (x; y) thỏa mãn: 3x + 4y - m = 0 . Khi đó hãy tính tổng tất cả các giá trị m tìm được?
A. 20
B. 46
C. 28
D. 14
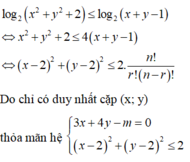
nên đường thẳng 3x + 4y - m = 0 là tiếp tuyến của đường tròn (x – 2)2 + (y – 2)2 = 2.
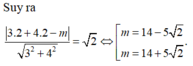
Chọn C.
Đúng 0
Bình luận (0)
Biết rằng trong tất cả các cặp (x;y) thỏa mãn
log
2
x
2
+
y
2
+
2
≤
log
2
x
+
y
-
1
chỉ có duy nhất một cặp (x;y) thỏa mãn 3x+4y-m0....
Đọc tiếp
Biết rằng trong tất cả các cặp (x;y) thỏa mãn log 2 x 2 + y 2 + 2 ≤ log 2 x + y - 1 chỉ có duy nhất một cặp (x;y) thỏa mãn 3x+4y-m=0. Khi đó hãy tính tổng tất cả các giá trị m tìm được.
A. 20
B. 28
C. 46
D. 14
Biết rằng trong tất cả các cặp (x; y) thỏa mãn:
log
2
x
2
+
y
2
+
2
≤
2
+
log
2
x
+
y
-
1
. Chỉ có duy nhất một cặp (x;...
Đọc tiếp
Biết rằng trong tất cả các cặp (x; y) thỏa mãn: log 2 x 2 + y 2 + 2 ≤ 2 + log 2 x + y - 1 . Chỉ có duy nhất một cặp (x; y) thỏa mãn: 3x + 4y - m = 0 . Khi đó hãy tính tổng tất cả các giá trị m tìm được?
A. 20
B. 46
C. 28
D. 14
Tìm tất cả các cặp số nguyên x, y thỏa mãn: x3 + x = y
a)Tìm tất cả các cặp số nguyên x, y thỏa mãn:x(2y+3)=y+1
b) Tìm tất cả các số nguyên của x thỏa mãn:(-1)+3(-5)+7 ...+ x = 2002
a) => 2xy +3x=y+1
=> 2xy+3x-y=1
=> x(2y+3) - 1/2 (2y+3) +3/2 =1
=> (x-1/2)(2y+3)=1-3/2= -1/2
=> (2x-1)(2y+3)=-1
ta có bảng
...........
Tìm tất cả các cặp số nguyên x,y sao cho : x-2xy + y = 0
\(\Rightarrow2x-4xy+2y=0\\ \Rightarrow2x\left(1-2y\right)+2y-1=-1\\ \Rightarrow2x\left(1-2y\right)-\left(1-2y\right)=-1\\ \Rightarrow\left(2x-1\right)\left(2y-1\right)=1=1.1=\left(-1\right)\left(-1\right)\)
Với \(\left\{{}\begin{matrix}2x-1=1\\2y-1=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\rightarrow\left(1;1\right)\)
Với \(\left\{{}\begin{matrix}2x-1=-1\\2y-1=-1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\rightarrow\left(0;0\right)\)
Vậy các cặp \(\left(x;y\right)\) cần tìm là \(\left(1;1\right);\left(0;0\right)\)
Đúng 3
Bình luận (0)
tìm tất cả các cặp số nguyên x, y thỏa mãn x2+x = 32019y+1
- Với \(y=0\Rightarrow x^2+x=3^0+1=2\)
\(\Rightarrow x^2+x-2=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
- Với \(y< 0\Rightarrow3^{2019y}\) không phải số nguyên \(\Rightarrow3^{2019y}+1\) không phải số nguyên (loại)
- Với \(y>0\Rightarrow3^{2019y}⋮3\Rightarrow3^{2019y}+1\) chia 3 dư 1
Mà \(x^2+x=x\left(x+1\right)\) là tích 2 số nguyên liên tiếp nên chia 3 chỉ có thể dư 0 hoặc 2
\(\Rightarrow x^2+x\ne3^{2019y}+1\) với mọi \(y>0\) \(\Rightarrow\) phương trình ko có nghiệm nguyên
Vậy pt đã cho có đúng 2 cặp nghiệm nguyên là \(\left(x;y\right)=\left(-2;0\right);\left(1;0\right)\)
Đúng 2
Bình luận (1)
@ Ha Dung vì khi y < 0 thì y = -k (k N)
⇒ 32019y = 3-2019k = ( N)
()2019k không phải là số nguyên vậy 32019y không phải là số nguyên em nhé.
Đúng 0
Bình luận (0)
Tìm tất cả các cặp số nguyên(x,y)thỏa mãn:2^x+1.3^y=12^x
Ta có : \(2^{x+1}.3^y=12^x\)
\(\Leftrightarrow3^y=\dfrac{12^x}{2^{x+1}}=\dfrac{3^x.4^x}{2^{x+1}}=\dfrac{3^x.2^{2x}}{2^{x+1}}=3^x.2^{2x}:2^{x+1}=3^x.2^{x-1}\)
\(\Leftrightarrow\dfrac{3^y}{3^x}=2^{x-1}\)
\(\Leftrightarrow3^{y-x}=2^{x-1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}y-x=0\\x-1=0\end{matrix}\right.\Leftrightarrow x=y=1\)(tm)
Vậy (x;y) = (1;1) nghiệm của phương trình trên
Đúng 1
Bình luận (0)
Tìm tất cả các cặp số nguyên x, y thỏa mãn:
8|x - 2017| = 25 - y2
\(8\left|x-2017\right|=25-y^{2\text{}}\)
\(\Leftrightarrow8\left|x-2017\right|+y^2=25=25+0=24+1=21+4=16+9\)
Mà \(8\left|x-2017\right|\) chẵn nên ta có các trường hợp sau:
TH1: \(\left\{{}\begin{matrix}8\left|x-2017\right|=0\\y^2=25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2017\\y=\pm5\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}8\left|x-2017\right|=24\\y^2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=2020\\x=2014\end{matrix}\right.\\y=\pm5\end{matrix}\right.\)
TH3: \(\left\{{}\begin{matrix}8\left|x-2017\right|=16\\y^2=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=2019\\x=2015\end{matrix}\right.\\y=\pm3\end{matrix}\right.\)
Đúng 1
Bình luận (0)