Tính tổng của 2 đa thức
P = x5 + xy + 0,3y2 – x2y3 – 2 và Q = x2y3 + 5 – 1,3y2.
Tính tổng của hai đa thức:
P = x5 + xy + 0,3y2 – x2y3 – 2 và Q = x2y3 + 5 – 1,3y2
Ta có: P = x5 + xy + 0,3y2 – x2y3 – 2
và Q = x2y3 + 5 – 1,3y2.
⟹ P + Q = (x5 + xy + 0,3y2 – x2y3 – 2) + (x2y3 + 5 – 1,3y2)
= x5 + xy + 0,3y2 – x2y3 – 2 + x2y3 + 5 – 1,3y2
= x5 +(– x2y3 + x2y3)+ (0,3y2 – 1,3y2)+ xy +(– 2 + 5)
= x5 + 0 – y2 + xy + 3.
= x5 – y2 + xy + 3.
Tính tổng của hai đa thức:
a) M = x2y + 0,5xy3 – 7,5x3y2 + x3 và N = 3xy3 – x2y + 5,5x3y2
b) P = x5 + xy + 0,3y2 – x2y3 – 2 và Q = x2y3 + 5 – 1,3y2
a)\(M+N=x^2y+0,5xy^3-7,5x^3y^2+x^3+3xy^3-x^2y+5,5x^3y^2=x^3+3,5xy^3-2x^3y^2\)b) \(P+Q=x^5+xy+0,3y^2-x^2y^3-2+x^2y^3+5-1,3y^2=x^5-y^2+xy+3\)
Tính giá trị của biểu thức x2y3 + xy tại x = 1 và y = 1/2.
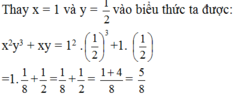
Vậy giá trị của biểu thức x2y3 + xy tại x = 1 và y = 1/2 là 5/8.
Tính giá trị của biểu thức :
A = x2y3 + xy tại x = - 1 và y = 2.
B = 2x2 + y4 + xyz – 5 tại x = 3 ; y = 2; z = 1.
Thay `x = -1 ; y = 2` vào `A`, có:
`A = (-1)^2 . 2^3 + (-1) . 2`
`A = 1 . 8 - 1 . 2 = 6`
________________________________
Thay `x = 3 ; y = 2 ; z = 1` vào `B`. Ta có:
`B = 2 . 3^2 + 2^4 + 3 . 2 . 1 - 5`
`B = 2 . 9 + 16 + 6 - 5`
`B = 18 + 16 + 6 - 5 = 35`
A=-1.2.2.3+-1.2
=-2.6+-2
=-12+-2
=-14
B=2.3.2+2.4+3.2.1.-5
=6.2+8+6.1.-5
=12+8+6.-5
=20+-30
=-10
Thay x=−1;y=2x=-1;y=2 vào A,
Ta có:A=(−1)2.23+(−1).2
A=(-1)2.23+(-1).2
A=1.8−1.2=6
A=1.8-1.2=6
________________________________
Thay x=3;y=2;z=1x=3;y=2;z=1 vào B.
Ta có:B=2.32+24+3.2.1−5
B=2.32+24+3.2.1-5
B=2.9+16+6−5B=2.9+16+6-5
B=18+16+6−5=35
Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:
Đa thức thu gọn của đa thức 1 / 2 x 2 y 3 - x 2 y 3 + 3 x 2 y 2 z 2 - z 4 - 3 x 2 y 2 z 2
A. - 1 / 2 x 2 y 3 - z 4 - 3 x 2 y 2 z 2
B. - 1 / 2 x 2 y 3 - z 4
C. 1 / 2 x 2 y 3 - z 4 - 6 x 2 y 2 z 2
D. 1 / 2 x 2 y 3 - z 4
Chọn B
Ta có: 1/2 x2y3 - x2y3+ 3x2y2z2- z4 - 3x2y2z2
= -1/2 x2y3 - z4.
Thu gọn các đa thức sau: 1/2 x2y3 – x2y3 + 3x2y2z2 – z4 – 3x2y2z2
1/2.x2y3 – x2y3 + 3x2y2z2 – z4 – 3x2y2z2
= (1/2.x2y3 – x2y3) + (3x2y2z2 – 3x2y2z2) – z4.
(1/2 - 1)x2.y3 + (3 - 3)x2y2z2 – z4
= - 1/2.x2y3 – z4
thu gọn đa thức và tìm bậc
3x4y2 + \(\dfrac{\text{1}}{\text{2}}\) xy5 - \(\dfrac{\text{3}}{\text{4}}\) x2y3 -
\(A=\left(3x^4y^2-\dfrac{1}{2}x^4y^2\right)+\left(\dfrac{1}{2}xy^5+5xy^5\right)+\left(\dfrac{-3}{4}x^2y^3-\dfrac{1}{4}x^2y^3\right)=\dfrac{11}{4}x^4y^2+\dfrac{26}{5}xy^5-x^2y^3\)
Bậc là 6
A = x2y3 + xy tại x = - 1 và y = 2.
B = 2x2 + y4 + xyz – 5 tại x = 3 ; y = 2; z = 1.
a: \(A=\left(-1\right)^2\cdot2^3+\left(-1\right)\cdot2=8-2=6\)
b: \(B=2\cdot2^2+2^4+3\cdot2\cdot1-5=8+16+6-5=8+16+1=25\)
Giá trị của biểu thức x 2 y 3 + x y tại x = 1,y = 1/2 là:
A. 1 4
B. 5 8
C. - 5 8
D. 3 4
Hợp chất X2Y3 có tổng số hạt cơ bản( proton,nơtron,electron) trong 1 phân tử là 152, trong đó số hạt không mang điện kém số hạt mang điện là 48. Nguyên tử khối của X lớn hơn nguyên tử khối của Y là 11.Xác định 2 nguyên tố X,Y và công thức X2Y3.
Có
+) 2(2pX + nX) + 3(2pY + nY) = 152
=> 4pX + 2nX + 6pY + 3nY = 152 (1)
+) (4.pX +6.pY)- (2nX + 3nY) = 48 (2)
+) pX + nX - pY - nY = 11 (3)
(1)(2) => \(\left\{{}\begin{matrix}2p_X+3p_Y=50\\2n_X+3n_Y=52\end{matrix}\right.\)
=> 2(pX + nX) + 3(pY + nY) = 102 (4)
(3)(4) => \(\left\{{}\begin{matrix}p_X+n_X=27=>A_X=27\left(Al\right)\\p_Y+n_Y=16=>A_Y=16\left(O\right)\end{matrix}\right.\)
=> CTHH: Al2O3