Lời giải: 

Ta có: \(\overrightarrow{MA}=(a-3;-1); \overrightarrow{MB}=(-3;b-1)\)

Để tam giác MAB vuông tại M thì: \(\overrightarrow{MA}\perp \overrightarrow{MB}\Leftrightarrow \overrightarrow{MA}.\overrightarrow{MB}=0\)

\(\Leftrightarrow -3(a-3)+(-1)(b-1)=0\)

\(\Leftrightarrow 3a+b=10\)

\(2S_{MAB}=|\overrightarrow{MA}|.|\overrightarrow{MB}|=\sqrt{(a-3)^2+1}.\sqrt{9+(b-1)^2}\)

\(=\sqrt{[(a-3)^2+1][9+(10-3a-1)^2}]=3\sqrt{[(a-3)^2+1][1+(a-3)^2]}=3[(a-3)^2+1]\geq 3\)

Vậy diện tích MAB nhỏ nhất khi \(a-3=0\Leftrightarrow a=3\)

\(a=3\Rightarrow b=10-3a=1\)

Vậy...........

Đầu tiên, ta cần tìm điểm cực trị của hàm số f(x) = x^3 - 3x^2 + m. Điều kiện cần và đủ để x_0 là điểm cực trị của hàm số y = f(x) là f’(x_0) = 0 và f’'(x_0) ≠ 0.

Ta có f’(x) = 3x^2 - 6x và f’'(x) = 6x - 6.

Giải phương trình f’(x) = 0, ta được x_1 = 0 và x_2 = 2. Kiểm tra điều kiện thứ hai, ta thấy f’‘(0) = -6 ≠ 0 và f’'(2) = 6 ≠ 0 nên x_1 = 0 và x_2 = 2 là hai điểm cực trị của hàm số.

Vậy, A = (0, f(0)) = (0, m) và B = (2, f(2)) = (2, 4 - m).

Trọng tâm G của tam giác OAB có tọa độ (x_G, y_G) = (1/3 * (x_A + x_B + x_O), 1/3 * (y_A + y_B + y_O)) = (2/3, 1/3 * (m + 4)).

Để G thuộc đường thẳng 3x + 3y - 8 = 0, ta cần có 3 * (2/3) + 3 * (1/3 * (m + 4)) - 8 = 0. Giải phương trình này, ta được m = 2.

Vậy, đáp án là B. m = 2.

Tham khảo ở đây nhé!

Trong mặt phẳng tọa độ Oxy cho điểm M(3;1). Giả sử A(a;0) và B(0;b) ( với a, b là các số thực không âm) là 2 điểm sao cho tam giác MAB vuông tại M và có diện tích nhỏ nhất. Tìm a và b

tóm lại đề bài bạn cần làm như sau

bạn tính vecto MA rồi tính vecto MB từ đó tính độ dài MA và MB

=>diện tích tam giác vuông MAB=1/2 MA.MB rồi lập luận thế thôi hết bài 

lập luận không khó đâu good luck

 \(\overrightarrow{MA}=\left(a-3;-1\right);\overrightarrow{MB}=\left(-3;b-1\right)\)

Theo gt tam giác ABM vuôg tại M nên :

\(S=\dfrac{1}{2}MA.MB=\dfrac{1}{2}\sqrt{\left(a-3\right)^2+\left(b-1\right)^2}=\dfrac{1}{2}\sqrt{\left(a-3\right)^2+1}\sqrt{3^2+\left(9-3a\right)^2}=\dfrac{3}{2}\left[\left(a-3\right)^2+1\right]\ge\dfrac{3}{2}\)

min S =3/2 khi a=3, ta đc b=1 Do vậy T = a²+ b² = 10

1, Ta có : y = mx - 2m - 1 

<=> m ( x - 2 ) - 1 - y = 0 

<=> m(x - 2) - (y+1) = 0

Dấu ''='' xảy ra khi x = 2 ; y = -1 

Vậy (d) luôn đi qua A(2;-1) 

2, (d) : y = mx - 2m - 1

Cho x = 0 => y = -2m - 1 

=> d cắt Oy tại A(0;-2m-1) 

=> OA = \(\left|-2m-1\right|\)

Cho y = 0 => x = \(\dfrac{2m+1}{m}\)

=> d cắt trục Ox tại B(2m+1/m;0) 

=> OB = \(\left|\dfrac{2m+1}{m}\right|\)

Ta có : \(S_{OAB}=\dfrac{1}{2}\left|\dfrac{2m+1}{m}.\left(-2m-1\right)\right|=2\)

\(\Leftrightarrow\left|-\dfrac{\left(2m+1\right)^2}{m}\right|=4\Leftrightarrow\left[{}\begin{matrix}-\dfrac{\left(2m+1\right)^2}{m}=4\\-\dfrac{\left(2m+1\right)^2}{m}=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4m^2+8m+1=0\\4m^2+1=0\left(voli\right)\end{matrix}\right.\)

<=> m = \(\dfrac{-2\pm\sqrt{3}}{2}\)

2: Tọa độ điểm A là:

\(\left\{{}\begin{matrix}y_A=0\\mx=2m+1\end{matrix}\right.\Leftrightarrow A\left(\dfrac{2m+1}{m};0\right)\)

Tọa độ điểm B là:

\(\left\{{}\begin{matrix}x=0\\y=-2m-1\end{matrix}\right.\Leftrightarrow B\left(-2m-1;0\right)\)

Theo đề, ta có: \(\left|\dfrac{4m^2+4m+1}{m}\right|=4\)

\(\Leftrightarrow\left[{}\begin{matrix}4m^2+4m+1=4m\\4m^2+4m+1=-4m\end{matrix}\right.\Leftrightarrow4m^2+8m+1=0\)

\(\Leftrightarrow4m^2+8m+4m-3=0\)

\(\Leftrightarrow\left(2m+2\right)^2=3\)

hay \(m\in\left\{\dfrac{\sqrt{3}-2}{2};\dfrac{-\sqrt{3}-2}{2}\right\}\)

Ta có 

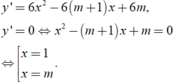
Để hàm số có hai điểm cực trị khi m khác -1

Tọa độ các điểm cực trị là A( 1; m³+ 3m-1) và B( m; 3m²)  

Suy ra

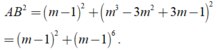
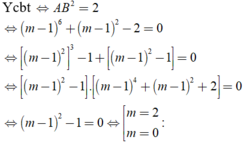
Chọn B.