Cho góc xoy khác góc bẹt , trên Ox lấy 2 điểm A và B , trên Oy lấy 2 điểm C và D sao cho OA=OC;OB=OD,BC cắt AD tại I.
Chứng minh rằng : a) AD = BC b)OI là phân giác của góc xOy c) AC//BD
Những câu hỏi liên quan
cho góc xOy khác góc bẹt. Trên Ox lấy A và B sao cho OA < OB. Trên Oy lấy 2 điểm C,D sao cho OA=OC, OB=OD cắt BC tại M
a) chứng minh OM vuông góc AC
b) chứng minh AC // BD
Xem chi tiết
Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B (A nằm giữa O và B). Trên Oy lấy hai điểm C và D (C nằm giữa O và D) sao cho OA = OC; OB = OD. CMR: AC // BD.
Câu hỏi của nguyenvandat - Toán lớp 7 - Học toán với OnlineMath
Cho góc x O y ^ khác góc bẹt. Trên tia Ox lấy hai điểm A và B, trên tia Oy lấy hai điểm C và D sao cho OA = OC và OB = OD. Gọi I là giao điểm của hai đoạn thẳng AD và BC. Khi đó
A. BC = AD
B. IA = IC
C. OI là tia phân giác của góc xOy
D. Cả A, B, C đều đúng.
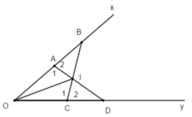
+ Giả sử A nằm giữa hai điểm O và B; C nằm giữa hai điểm O và D
Do đó ta có: OA + AB = OB; OC + CD = OD
Mà OA = OC; OB = OD (gt)
Nên AB = CD
+ Xét tam giác OAD và tam giác OCB có:
OA = OC; OB = OD (gt)
x O y ^ góc chung
Do đó: Δ O A D = Δ O C B (c – g – c)


Đáp án D
Đúng 0
Bình luận (0)
Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B, trên tia Oy lấy hai điểm C và D sao cho OA = OC, OB = OD. Gọi I là giao điểm của hai đoạn thẳng AD và BC. Chứng minh rằng:
BC = AD;
a) ΔAOD và ΔCOB có:
OA = OC (giả thiết)
Góc O chung
OD = OB (giả thiết)
⇒ ΔAOD = ΔCOB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
Đúng 0
Bình luận (0)
Bài 5: Cho xOy khác góc bẹt. Trển Ox lấy các điểm A và B sao cho A nằm giữa O và B. Trên tia Oy lấy các điểm C và D sao cho OA = OC, AB = CD. Chứng minh AC// BD.
Xét ΔOBD có
OA/OB=OC/OD
Do đó: CA//BD
Đúng 0
Bình luận (0)
Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B, trên tia Oy lấy hai điểm C và D sao cho OA = OC, OB = OD. Gọi I là giao điểm của hai đoạn thẳng AD và BC. Chứng minh rằng:
Tia OI là tia phân giác của góc xOy.
Ta có: ΔOIA và ΔOIC có
OI chung
IA = IC (chứng minh trên)
OA = OC (giả thiết)
ΔOIA = ΔOIC (c.c.c)
Đúng 0
Bình luận (0)
Bài 3.(4 điểm) Cho góc xOy khác góc bẹt. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA OB. Trên tia phân giác Ot của góc xOy lấy điểm C sao cho OC OA.a) Vẽ hình và viết giả thiết, kết luận. b) Chứng minh tam giác OAC tam giác OBC. c) Gọi M là giao điểm của AB và OC. Chứng minh M là trung điểm của đoạn thẳng AB. d) Chứng minhOM vuông góc AB. GIÚP MIK NHANH VS Ạ :D
Đọc tiếp
Bài 3.(4 điểm) Cho góc xOy khác góc bẹt. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Trên tia phân giác Ot của góc xOy lấy điểm C sao cho OC > OA.a) Vẽ hình và viết giả thiết, kết luận. b) Chứng minh tam giác OAC= tam giác OBC. c) Gọi M là giao điểm của AB và OC. Chứng minh M là trung điểm của đoạn thẳng AB. d) Chứng minhOM vuông góc AB. GIÚP MIK NHANH VS Ạ :D
cho góc xoy khác góc bẹt .trên tia ox lấy hai điểm A và B .trên tia oy lấy hai điểm C và D sao cho OA=OC,OB=OD.chứng minh rằng:a,Tam giác OAD=Tam giác OCB. b,Tam giác ACD=Tam giác CAB.
Ta có hình vẽ:
a/ Xét tam giác OAD và tam giác OCB có
-O : góc chung
-OA = OC
-OB = OD
=> tam giác OAD = tam giác OCB
b/ Xét tam giác ACD và tam giác CAB có
-AC: cạnh chung
-OA = OC
OB = OD
\(\Rightarrow\)AB = CD
-AD = CB (vì \(\Delta\)OAD=\(\Delta\)OCB)
Vậy tam giác ACD = tam giác CAB
Đúng 1
Bình luận (0)
Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B, trên tia Oy lấy hai điểm C và D sao cho OA = OC, OB = OD. Gọi I là giao điểm của hai đoạn thẳng AD và BC. Chứng minh rằng:
IA = IC, IB = ID
- ΔAOD = ΔCOB
Lại có: OA = OC, OB = OD ⇒ OB – OA = OD – OC hay AB = CD.
- Xét ΔDIC và ΔBIA có:
CD = AB (chứng minh trên)
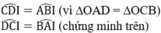
⇒ ΔDIC = ΔBIA (g.c.g)
⇒ IC = IA và ID = IB (các cặp cạnh tương ứng)
Đúng 0
Bình luận (0)
Cho góc xOy khác góc bẹt . Trên cạnh Ox lấy các điểm A,B (OA nhỏ hơn OB ) trên cạnh Oy lấy các điểm C,D sao cho OC=OA,OD=OB. Chứng minh rằng :
a) AD=BC
Lm hộ mik ![]() với !
với !


















