Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt P O M ^ ; O M = R 0 ≤ α ≤ π 3 ; R > 0 Gọi V là khối tròn xoay thu được khi quay tam giác đó quanh trục Ox (H.63).
Tính thể tích của V theo α và R
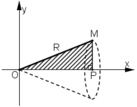
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt P O M ^ ; O M = R 0 ≤ α ≤ π 3 ; R > 0 Gọi V là khối tròn xoay thu được khi quay tam giác đó quanh trục Ox (H.63).
Tìm α sao cho thể tích V lớn nhất
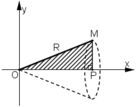
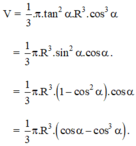
* Ta tìm giá trị lớn nhất của P = cosα – cos3α
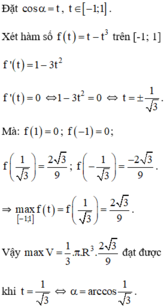
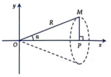
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox, cạnh huyền OM không đổi, O M = R R > 0 . Tính theo R giá trị lớn nhất của thể tích khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox.
A. 2 3 πR 3 27
B. 2 3 πR 3 9
C. 2 2 πR 3 27
D. 2 2 πR 3 9
Đáp án A.
Tam giác OPM vuông tại P suy ra O P = R . cos α ; M P = R . sin α .
Thể tích khối nón được tính bằng công thức
V = 1 3 . O P . πMP 2 = 1 3 . R . cosα . π . R 2 . sin 2 α = πR 3 3 . cosα . sin 2 α = πR 3 3 . cosα 1 - cos 2 α
V đạt giá trị lớn nhất khi - cos 3 α + cos α đạt giá trị lớn nhất.
Sử dụng TABLE ta có

Ta thấy hàm số đạt giá trị lớn nhất là 0 , 384 = 2 3 9 . Suy ra V = 2 3 πR 3 27 .
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox, cạnh huyền OM không đổi, O M = R ( R>0 ). Tính theo R giá trị lớn nhất của thể tích khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox.
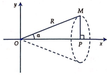
A. 2 3 π R 3 27
B. 2 3 π R 3 9
C. 2 2 π R 3 27
D. 2 2 π R 3 9
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt \(\widehat{POM}=\alpha;OM=R\left(0\le\alpha\le\dfrac{\pi}{3};R>0\right)\)
Gọi V là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox (H.63)
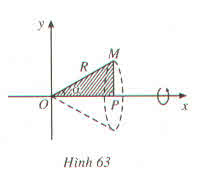
a) Tính thể tích của V theo \(\alpha\) và R
b) Tìm \(\alpha\) sao cho thể tích của V lớn nhất
a) Hoành độ điểm P là :
xp = OP = OM. cos α = R.cosα
Phương trình đường thẳng OM là y = tanα.x. Thể tích V của khối tròn xoay là:
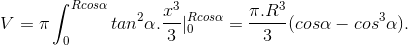
b) Đặt t = cosα => t ∈ 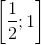 . (vì α ∈
. (vì α ∈ 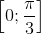 ), α = arccos t.
), α = arccos t.
Ta có :
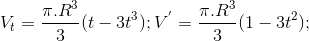
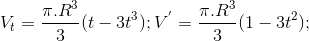
V' = 0 ⇔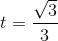
hoặc 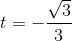 (loại).
(loại).
Từ đó suy ra V(t) lớn nhất ⇔ 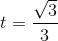 , khi đó :
, khi đó : 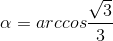 .
.
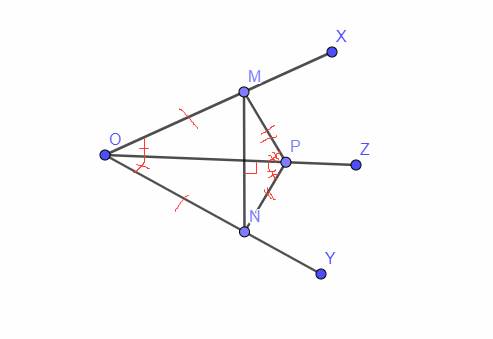
Cho tia xOy , Oz là tia phân giác của góc xOy . Điểm M nằm trên tia Ox, điểm N trên tia Oy sao cho OM= ON . a, chứng minh tam giác OMP= tam giác ONP. b, Gọi H là giao điểm của MN và OP, chứng minh MN vuông góc với OP
#\(N\)
`a,` Xét Tam giác `OMP` và Tam giác `ONP` có:
`OM = ON (g``t)`
\(\widehat{MOP}=\widehat{NOP}\) `(` tia phân giác \(\widehat{xOy}\) `)`
`OP` chung
`=>` Tam giác `OMP =` Tam giác `ONP (c-g-c)`
`b,` Vì Tam giác `OMP =` Tam giác `ONP (a)`
`=> MP = NP (` 2 cạnh tương ứng `)`
`=>`\(\widehat{MPH}=\widehat{NPH}\) `(` 2 góc tương ứng `)`
Xét Tam giác `MPH` và Tam giác `NPH` có:
`MP = NP (CMT)`
\(\widehat{MPH}=\widehat{NPH}(CMT)\)
`PH` chung
`=>` Tam giác `MPH = `Tam giác `NPH (c-g-c)`
`=>`\(\widehat{MHP}=\widehat{NHP}\) `(` 2 góc tương ứng `)`
Mà `2` góc này ở vị trí kề bù
`=>`\(\widehat{MHP}+\widehat{NHP}=180^0\)
`=>` \(\widehat{MHP}=\widehat{NHP}=\)\(\dfrac{180}{2}=90^0\)
`=>`\(MN\perp OP\left(đpcm\right)\)
Ở mặt nước, một nguồn sóng đặt tại điểm O dao động điều hòa theo phương thẳng đứng. Sóng truyền trên mặt nước có bước sóng λ. Chọn hệ tọa độ vuông góc Oxy (thuộc mặt nước). Hai điểm P và Q nằm trên Ox, P dao động ngược pha với O còn Q dao động cùng pha với O. Giữa khoảng OP có 4 điểm dao động ngược pha với O, giữa khoảng OQ có 8 điểm dao động ngược pha với O. Trên trục Oy có điểm M sao cho góc PMQ đạt giá trị lớn nhất. Tìm số điểm dao động ngươc pha với O trên đoan MQ
A. 5.
B. 4
C. 6.
D. 7.
Trong mặt phẳng toạ độ Oxy, cho tam giác MNP vuông tại M. Biết điểm M(2,1); N(3,-2) và P là điểm nằm trên trục Ox. Tìm toạ độ điểm P và tính diện tích tam giác MNP
Do P thuộc Ox nên tọa độ có dạng \(P\left(p;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MN}=\left(1;-3\right)\\\overrightarrow{MP}=\left(p-2;-1\right)\end{matrix}\right.\)
Do tam giác MNP vuông tại M \(\Rightarrow\overrightarrow{MN}.\overrightarrow{MP}=0\)
\(\Rightarrow1.\left(p-2\right)+3=0\) \(\Rightarrow p=-1\)
\(\Rightarrow P\left(-1;0\right)\)
\(\Rightarrow\overrightarrow{MP}=\left(-3;-1\right)\Rightarrow\left\{{}\begin{matrix}MN=\sqrt{1^2+\left(-3\right)^2}=\sqrt{10}\\MP=\sqrt{\left(-3\right)^2+\left(-1\right)^2}=\sqrt{10}\end{matrix}\right.\)
\(\Rightarrow S_{MNP}=\dfrac{1}{2}MN.MP=5\)
Cho góc vuông xOy. Trên cạnh Ox lấy điểm A sao cho OA = 2cm. Điểm N di động trên cạnh Oy. Vẽ tam giác AMN vuông cân ở A sao cho M nằm trong góc vuông xOy. Hỏi điểm M di động trên đường nào?