Các câu hỏi tương tự
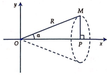
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox, cạnh huyền OM không đổi,
O
M
R
R
0
. Tính theo R giá trị lớn nhất của thể tích khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox. A.
2
3
πR
3
27
B.
2...
Đọc tiếp
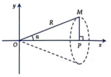
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox, cạnh huyền OM không đổi, O M = R R > 0 . Tính theo R giá trị lớn nhất của thể tích khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox.
A. 2 3 πR 3 27
B. 2 3 πR 3 9
C. 2 2 πR 3 27
D. 2 2 πR 3 9
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y sinx.cosx, trục tung, trục hoành và đường thẳng x π/2 . Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox. A. V π/16. B.
V
π
2
16
C.
V
π
2
+
π...
Đọc tiếp
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y =sinx.cosx, trục tung, trục hoành và đường thẳng x =π/2 . Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A. V =π/16.
B. V = π 2 16
C. V = π 2 + π 16
D. V = π 2 4
Cho hình phẳng (D) được giới hạn bởi các đường
x
0
,
x
π
,
y
0
và
y
−
sin
x
. Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức: A.
V
π
∫
0
π
sin...
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x = 0 , x = π , y = 0 và y = − sin x . Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức:
A. V = π ∫ 0 π sin x d x .
B. V = π ∫ 0 π sin 2 x d x .
C. V = π ∫ 0 π − sin x d x .
D. V = ∫ 0 π sin 2 x d x .
Thể tích khối tròn xoay gây nên bởi hình tròn
x
2
+
(
y
−
a
)
2
≤
R
2
(
0
R
a
)
khi quay quanh trục Ox là: A.
8
π
2
a
R
2
B....
Đọc tiếp
Thể tích khối tròn xoay gây nên bởi hình tròn x 2 + ( y − a ) 2 ≤ R 2 ( 0 < R < a ) khi quay quanh trục Ox là:
A. 8 π 2 a R 2
B. 4 π 2 a R 2
C. π 2 a R 2
D. 2 π 2 a R 2
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h = 3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P = R + 2r.
A. 2 3
B. 3
C. 3 3
D. 2
Xét các tam giác ABC nhọn nội tiếp đường tròn (O;R). Gọi
V
1
,
V
2
và
V
3
lần lượt là thể tích của các khối tròn xoay sinh ra khi quay tam giác OCA quanh trung trực của đoạn thẳng CA, quay tam giác OAB quanh trung trực của đoạn thẳng AB và quay tam giác OBC quanh trung trực của đoạn thẳng BC. Tính
V
3
theo R khi biểu thức
V
1...
Đọc tiếp
Xét các tam giác ABC nhọn nội tiếp đường tròn (O;R). Gọi V 1 , V 2 và V 3 lần lượt là thể tích của các khối tròn xoay sinh ra khi quay tam giác OCA quanh trung trực của đoạn thẳng CA, quay tam giác OAB quanh trung trực của đoạn thẳng AB và quay tam giác OBC quanh trung trực của đoạn thẳng BC. Tính V 3 theo R khi biểu thức V 1 + V 2 đạt giá trị lớn nhất.
A. V 3 = 2 π 3 9 R 3
B. V 3 = 8 π 81 R 3
C. V 3 = 2 2 81 π R 3
D. V 3 = 18 − 6 2 9 π R 3
Xét các tam giác ABC nhọn nội tiếp đường tròn
O
;
R
. Gọi
V
1
,
V
2
và
V
3
lần lượt là thể tích của các khối tròn xoay sinh ra khi quay tam giác OCA quanh trung trực của đoạn thẳng CA, quay tam giác OAB quanh trung trực của đoạn thẳng AB và quay tam giác OBC quanh trung trực của đoạn thẳng...
Đọc tiếp
Xét các tam giác ABC nhọn nội tiếp đường tròn O ; R . Gọi V 1 , V 2 và V 3 lần lượt là thể tích của các khối tròn xoay sinh ra khi quay tam giác OCA quanh trung trực của đoạn thẳng CA, quay tam giác OAB quanh trung trực của đoạn thẳng AB và quay tam giác OBC quanh trung trực của đoạn thẳng BC. Tính V 3 theo R khi biểu thức V 1 + V 2 đạt giá trị lớn nhất.
A. V 3 = 2 π 3 9 R 3
B. V 3 = 8 π 81 R 3
C. V 3 = 2 2 81 π R 3
D. V 3 = 18 − 6 2 9 π R 3
Cho tam giác ABC có đường tròn nội tiếp
O
;
r
, cắt bỏ phần hình tròn và cho hình phẳng thu được quay quanh AO. Tính thể tích khối tròn xoay thu được theo r. A.
5
3
π
r
3
B.
4
3
π
r
3...
Đọc tiếp
Cho tam giác ABC có đường tròn nội tiếp O ; r , cắt bỏ phần hình tròn và cho hình phẳng thu được quay quanh AO. Tính thể tích khối tròn xoay thu được theo r.
A. 5 3 π r 3
B. 4 3 π r 3
C. π r 3 3
D. π r 3
Cho một vật thể nằm giữa hai mặt phẳng x0,
x
π
biết rằng mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
x
0
≤
x
≤
π
cắt vật thể theo thiết diện là một tam giác đều cạnh
2
sin
x
Thể tích của vật thể đó là A.
3
π
2
B.
2...
Đọc tiếp
Cho một vật thể nằm giữa hai mặt phẳng x=0, x = π biết rằng mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ π cắt vật thể theo thiết diện là một tam giác đều cạnh 2 sin x Thể tích của vật thể đó là
A. 3 π 2
B. 2 3
C. 3 2
D. 2 π 3